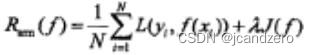机器学习学习笔记-多项式中的过拟合，泛化能力等

引用于

机器学习中模型泛化能力和过拟合现象(overfitting)的矛盾、以及其主要缓解方法正则化技术原理初探 - 郑瀚Andrew.Hann - 博客园 (cnblogs.com)

说在前面的一点东西

经验风险最小化最优模型

 结构风险最小化 structure risk minimization，为防止过拟合提出的策略，等价于正则化（regularization），加入正则化项regularizer，或罚项 penalty term：

产生过拟合和（over-fitting）和效果不好的原因

我们以一个简单的回归问题开始，说明许多关键的概念。 假设我们观察到一个实值输入变量x，我们想使用这个观察来预测实值目标变量t的值。

对于这个目的，一个很好的方法是考虑一个使用已知的产生方式人工制造出的例子，因为这样我们就知道生成数据的精确过程（动力学过程），从而能够和我们学习到得模型进行比较。这个例子的数据由函数sin(2πx)产生，目标变量带有随机的噪声。

现在假设给定一个训练集。这个训练集由x的N次观测组成，写作：

x ≡ (x1，...，xN)T

伴随着对应的t的观测值，记作：

t ≡ (t1，...，tN)T

下图展示了由N = 10个数据点组成的图像：

目标数据集t的获得方式是：

• 首先计算函数sin(2πx)的对应的值。
• 然后给每个点增加一个小的符合高斯分布的随机噪声，从而得到对应的tn的值。

通过使用这种方式产生数据，我们利用了许多真实数据集合的一个性质，即它们拥有一个内在的规律，这个规律是我们想要学习的，但是独自的观察被随机噪声干扰。

这种噪声可能由一个本质上随机的过程产生，例如放射性衰变，但是更典型的情况是由于存在没有被观察到的具有变化性的噪声源。

我们的目标是利用这个训练集预测对于输入变量的新值 x 的目标变量的值 t。

这涉及到隐式地发现内在的函数sin(2πx)。这本质上是一个困难的问题，因为我们不得不从有限的数据中生成模型。

因为观察到的数据被噪声干扰，因此对于一个给定的 x，合适的 t 值具有不确定性。

现在，我们用一种相当非正式的、相当简单的方式来进行曲线拟合：

其中M是多项式的阶数(order)，xj 表示 x 的 j 次幂。多项式系数 w0，...，wM 整体记作向量w。 

注意，虽然多项式函数 y(x, w)是 x 的一个非线性函数，它是系数w的一个线性函数。这一点对后面我们理解因为训练集不充分导致最优解不唯一问题有帮助。

系数的值可以通过调整多项式函数拟合训练数据的方式确定。这可以通过最小化误差函数 (error function)的方法实现。 

我们可以通过选择使得 E(w) 尽量小的 w 来解决曲线拟合问题。由于误差函数是系数 w 的二次函数，因此它关于系数的导数是 w 的线性函数，所以误差函数的最小值有一个唯一解，记作w∗，可以用解析的方式求出。

最终的多项式函数由函数y(x, w∗)给出。这是一个纯数学问题，没有什么好特别讨论的。我们本文的重点是讨论过拟合问题，过拟合问题和阶数 M 紧密相关。

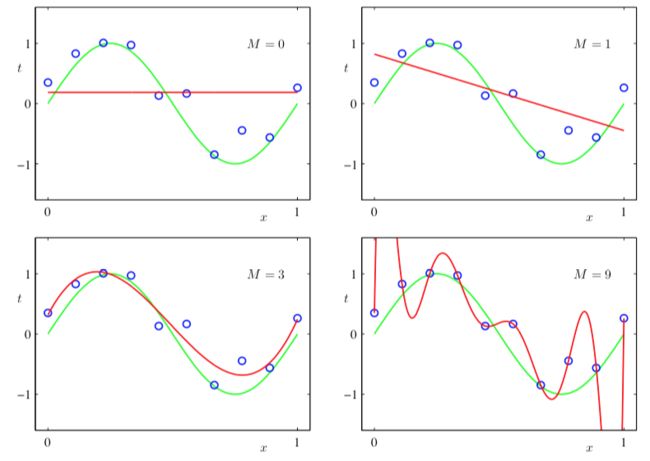
在下图中，我 们给出了4个拟合多项式的结果。多项式的阶数分别为M = 0, 1, 3, 9：

不同阶数的多项式曲线，用红色曲线表示，绿色表示原始目标函数曲线

我们注意到：

• 常数(M = 0)，和一阶(M = 1)多项式对于数据的拟合效果相当差，很难代表函数sin(2πx)。
• 三阶(M = 3)多项式似乎给出了对函数sin(2πx)的最好的拟合。
• 当我们达到更高阶的多项式(M = 9)，我们似乎得到了对于训练数据的一个完美的拟合。事实上，多项式函数精确地通过了每一个数据点，E(w∗) = 0。然而，拟合的曲线剧烈震荡，就表达函数sin(2πx)而言表现很差。这种行为叫做过拟合(over-fitting)。 

正如我们之前提到的，机器学习的目标是通过对新数据的预测实现良好的泛化性。

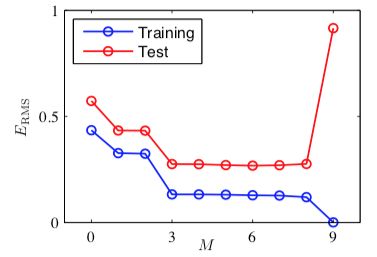
我们可以定量考察模型的泛化性与 M 的关系。考察的方式为：考虑一个额外的测试集，这个测试集由100个数据点组成，这100个数据点的生成方式与训练集的生成方式完全相同，但是在目标值中包含的随机噪声的值不同。对于每个M的选择，我们计算训练集和测试集的误差：
 

• 小的 M 值会造成较大的测试集误差，这可以归因于对应的多项式函数相当不灵活，不能够反映出sin(2πx)的震荡。
• 当 M 的取值为3 ≤ M ≤ 8时，测试误差较小，对于生成函数sin(2πx)也能给出合理的模拟。 
• 对于 M = 9的情形，训练集的误差为0，这符合我们的预期，因为此时的多项式函数有10个自由度，对应于10个系数w0, . . . , w9，所以可以调节模型的参数，使得模型与训练集中的10个数据点精确匹配。然而，正如我们在上图中看到的那样，测试集误差变得非常大，对应的函数y(x, w∗)表现出剧烈的震荡。 

发生这个情况的原因

题的原因可以被归纳为两句话：

• 训练集的不充分，导致了目标函数非唯一解的问题。这方面的讨论可以参阅另一个文章。
• 而随机噪声的存在，以及过度复杂的模型，导致了过拟合问题的发生，即模型过度地进行了调参。同时，训练集不充分问题，又加剧了过拟合。

由此，我们可以得出第一个直觉判断：

有效控制模型复杂度，可以有效缓解过拟合问题 

很有趣的

对已一个给定的模型复杂度，当数据集的规模增加时，过拟合问题变得不那么严重

0. 什么是泛化能力？如何评估

泛化能力是模型对未知数据的预测能力。大白话来说就是，模型训好了，放到实际场景中去使用，会不会掉链子，还是能达到跟训练时一样的效果。泛化能力的本质就是反映模型有没有对客观世界做真实的刻画，还是发生了过拟合。

泛化能力的评估，说简单很简单，搞个测试集测一下就可以了。
作者：迪丽娜扎
链接：https://www.jianshu.com/p/849423297c7f
来源：简书
 

2. 偏差与方差 - 机器学习算法泛化性能分析

在一个项目中，我们通过设计和训练得到了一个model，该model的泛化可能很好，也可能不尽如人意，其背后的决定因素是什么呢？或者说我们可以从哪些方面去改进从而使下次得到的model更加令人满意呢？

”偏差-方差分解（bias-variance decomposition）“是解释学习算法泛化能力性能的一种重要工具。偏差-方差分解试图对学习算法的期望泛化错误率进行拆解。

假设测试样本为x，yd 为 x 在数据集中的标记（注意，有可能出现噪声使得 yd != y，即所谓的打标样本不纯），y 为 x 的真实标记，f（x；D）为在训练集 D 上训练得到的模型 f 在 x 上的预测输出。

以回归任务为例，学习算法的期望预测为：

上式可被分解为：

整理得：

即，泛化误差可分解为：偏差、方差、噪声之和。