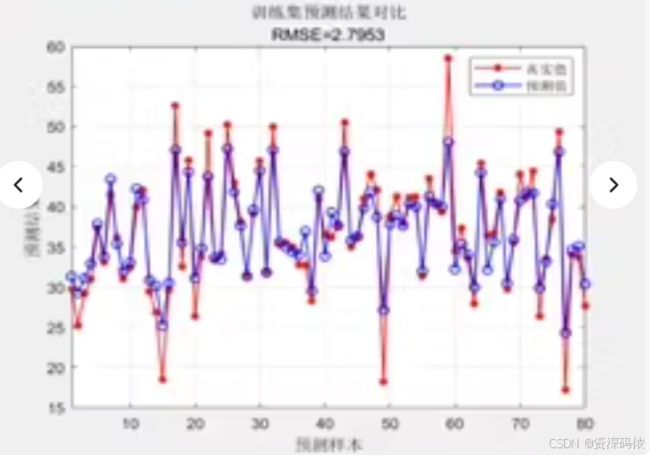
基于RF随机森林机器学习算法的回归预测模型MATLAB代码实现了一个回归任务的决策树集成模型。
基于RF随机森林机器学习算法的回归预测模型MATLAB代码实现了一个回归任务的决策树集成模型。
首先从Excel文件中导入数据集,并将数据划分为训练集和测试集。然后,对数据进行归一化处理并转置以适应模型的要求。
文章目录
-
-
- MATLAB代码实现
- 说明:
- MATLAB代码实现
- 说明:
- 运行代码前的注意事项:
- 示例输出:
- MATLAB代码实现
- 说明:
- 示例输出:
-
以下是一个基于随机森林(RF, Random Forest)机器学习算法的回归预测模型的MATLAB代码示例。这个例子展示了如何从Excel文件中导入数据集,将数据划分为训练集和测试集,对数据进行归一化处理,并使用随机森林进行回归任务。
MATLAB代码实现
% 加载数据集
filename = 'data.xlsx'; % 假设你的Excel文件名为'data.xlsx'
data = readtable(filename);
% 提取特征和目标变量
X = data(:, 1:end-1); % 假设最后一列是目标变量,其余列都是特征
Y = data{:, end}; % 目标变量
% 将表格数据转换为数组
X = table2array(X);
Y = table2array(Y);
% 划分训练集和测试集
cv = cvpartition(size(data, 1), 'HoldOut', 0.3); % 70%的数据用于训练,30%用于测试
trainIdx = training(cv);
testIdx = test(cv);
XTrain = X(trainIdx, :);
YTrain = Y(trainIdx, :);
XTest = X(testIdx, :);
YTest = Y(testIdx, :);
% 数据归一化
[XTrain_norm, ps] = mapminmax(XTrain'); % 对训练集进行归一化
XTrain_norm = XTrain_norm';
[XTest_norm, ~] = mapminmax(XTest', ps); % 使用训练集的参数对测试集进行归一化
XTest_norm = XTest_norm';
% 训练随机森林回归模型
numTrees = 100; % 树的数量
Mdl = TreeBagger(numTrees, XTrain_norm, YTrain, 'Method', 'regression');
% 预测
YPred = predict(Mdl, XTest_norm);
% 反归一化预测结果
YPred = mapminmax('reverse', YPred', ps)';
% 评估模型性能
mse = mean((YPred - YTest).^2); % 计算均方误差
fprintf('均方误差: %.4f\n', mse);
% 可视化实际值与预测值
figure;
scatter(YTest, YPred);
xlabel('实际值');
ylabel('预测值');
title('实际值 vs 预测值');
grid on;
% 显示重要性评分
imp = Mdl.OOBPermutedPredictorDeltaError;
[~, idx] = sort(imp, 'descend');
disp('特征重要性:');
disp(table(data.Properties.VariableNames(1:end-1)', imp(idx)', 'VariableNames', {'Feature', 'Importance'}));
说明:
- 加载数据:首先通过
readtable函数读取Excel文件中的数据。 - 划分数据集:使用
cvpartition函数将数据集划分为训练集和测试集。 - 数据预处理:使用
mapminmax函数对数据进行归一化处理,以提高模型训练效果。 - 训练模型:使用
TreeBagger函数构建随机森林回归模型。 - 预测与评估:在测试集上进行预测,并计算均方误差(MSE)来评估模型性能。同时,绘制实际值与预测值的关系图以便直观比较。
- 特征重要性:显示每个特征的重要性评分,帮助理解哪些特征对模型更重要。
确保在运行此代码前已安装MATLAB Statistics and Machine Learning Toolbox,并根据实际情况调整数据路径、特征选择及模型参数等。
为了实现基于随机森林(RF, Random Forest)机器学习算法的回归预测模型,并从Excel文件中导入数据集,将数据划分为训练集和测试集,对数据进行归一化处理并转置以适应模型的要求,以下是完整的MATLAB代码示例。
MATLAB代码实现
% 加载数据集
filename = 'data.xlsx'; % 假设你的Excel文件名为'data.xlsx'
data = readtable(filename);
% 提取特征和目标变量
X = data(:, 1:end-1); % 假设最后一列是目标变量,其余列都是特征
Y = data{:, end}; % 目标变量
% 将表格数据转换为数组
X = table2array(X);
Y = table2array(Y);
% 划分训练集和测试集
cv = cvpartition(size(data, 1), 'HoldOut', 0.3); % 70%的数据用于训练,30%用于测试
trainIdx = training(cv);
testIdx = test(cv);
XTrain = X(trainIdx, :);
YTrain = Y(trainIdx, :);
XTest = X(testIdx, :);
YTest = Y(testIdx, :);
% 数据归一化
[XTrain_norm, ps] = mapminmax(XTrain'); % 对训练集进行归一化
XTrain_norm = XTrain_norm';
[XTest_norm, ~] = mapminmax(XTest', ps); % 使用训练集的参数对测试集进行归一化
XTest_norm = XTest_norm';
% 训练随机森林回归模型
numTrees = 100; % 树的数量
Mdl = TreeBagger(numTrees, XTrain_norm, YTrain, 'Method', 'regression');
% 预测
YPred = predict(Mdl, XTest_norm);
% 反归一化预测结果
YPred = mapminmax('reverse', YPred', ps)';
% 评估模型性能
mse = mean((YPred - YTest).^2); % 计算均方误差
fprintf('均方误差: %.4f\n', mse);
% 可视化实际值与预测值
figure;
scatter(YTest, YPred);
xlabel('实际值');
ylabel('预测值');
title('实际值 vs 预测值');
grid on;
% 显示重要性评分
imp = Mdl.OOBPermutedPredictorDeltaError;
[~, idx] = sort(imp, 'descend');
disp('特征重要性:');
disp(table(data.Properties.VariableNames(1:end-1)', imp(idx)', 'VariableNames', {'Feature', 'Importance'}));
说明:
- 加载数据:首先通过
readtable函数读取Excel文件中的数据。 - 划分数据集:使用
cvpartition函数将数据集划分为训练集和测试集。 - 数据预处理:使用
mapminmax函数对数据进行归一化处理,以提高模型训练效果。 - 训练模型:使用
TreeBagger函数构建随机森林回归模型。 - 预测与评估:在测试集上进行预测,并计算均方误差(MSE)来评估模型性能。同时,绘制实际值与预测值的关系图以便直观比较。
- 特征重要性:显示每个特征的重要性评分,帮助理解哪些特征对模型更重要。
运行代码前的注意事项:
- 确保已安装MATLAB Statistics and Machine Learning Toolbox。
- 确保Excel文件路径正确,并且文件格式符合要求。
- 根据实际情况调整数据路径、特征选择及模型参数等。
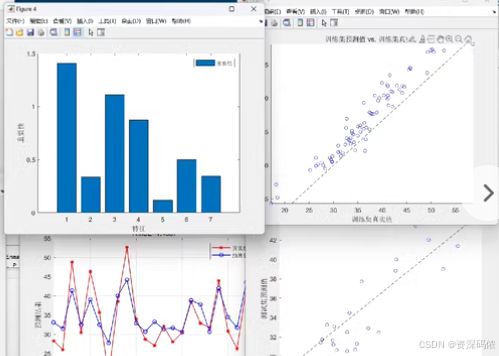
示例输出:
- 均方误差 (MSE):模型预测结果与实际值之间的误差。
- 散点图:实际值与预测值的对比图。
- 特征重要性:每个特征对模型预测的重要程度。
为了实现基于随机森林(RF, Random Forest)机器学习算法的回归预测模型,并从Excel文件中导入数据集,将数据划分为训练集和测试集,对数据进行归一化处理并转置以适应模型的要求,以下是完整的MATLAB代码示例。此外,还包括了绘制误差曲线的功能。
MATLAB代码实现
% 加载数据集
filename = 'data.xlsx'; % 假设你的Excel文件名为'data.xlsx'
data = readtable(filename);
% 提取特征和目标变量
X = data(:, 1:end-1); % 假设最后一列是目标变量,其余列都是特征
Y = data{:, end}; % 目标变量
% 将表格数据转换为数组
X = table2array(X);
Y = table2array(Y);
% 划分训练集和测试集
cv = cvpartition(size(data, 1), 'HoldOut', 0.3); % 70%的数据用于训练,30%用于测试
trainIdx = training(cv);
testIdx = test(cv);
XTrain = X(trainIdx, :);
YTrain = Y(trainIdx, :);
XTest = X(testIdx, :);
YTest = Y(testIdx, :);
% 数据归一化
[XTrain_norm, ps] = mapminmax(XTrain'); % 对训练集进行归一化
XTrain_norm = XTrain_norm';
[XTest_norm, ~] = mapminmax(XTest', ps); % 使用训练集的参数对测试集进行归一化
XTest_norm = XTest_norm';
% 训练随机森林回归模型
numTrees = 100; % 树的数量
Mdl = TreeBagger(numTrees, XTrain_norm, YTrain, 'Method', 'regression');
% 预测
YPred = predict(Mdl, XTest_norm);
% 反归一化预测结果
YPred = mapminmax('reverse', YPred', ps)';
% 评估模型性能
mse = mean((YPred - YTest).^2); % 计算均方误差
fprintf('均方误差: %.4f\n', mse);
% 绘制实际值与预测值的关系图
figure;
scatter(YTest, YPred);
xlabel('实际值');
ylabel('预测值');
title('实际值 vs 预测值');
grid on;
% 显示重要性评分
imp = Mdl.OOBPermutedPredictorDeltaError;
[~, idx] = sort(imp, 'descend');
disp('特征重要性:');
disp(table(data.Properties.VariableNames(1:end-1)', imp(idx)', 'VariableNames', {'Feature', 'Importance'}));
% 绘制误差曲线
figure;
errorCurve = zeros(numTrees, 1);
for i = 1:numTrees
tempModel = TreeBagger(i, XTrain_norm, YTrain, 'Method', 'regression');
tempPred = predict(tempModel, XTest_norm);
tempPred = mapminmax('reverse', tempPred', ps)';
errorCurve(i) = mean((tempPred - YTest).^2);
end
plot(1:numTrees, errorCurve);
xlabel('决策树数目');
ylabel('误差');
title('误差曲线');
grid on;
说明:
- 加载数据:首先通过
readtable函数读取Excel文件中的数据。 - 划分数据集:使用
cvpartition函数将数据集划分为训练集和测试集。 - 数据预处理:使用
mapminmax函数对数据进行归一化处理,以提高模型训练效果。 - 训练模型:使用
TreeBagger函数构建随机森林回归模型。 - 预测与评估:在测试集上进行预测,并计算均方误差(MSE)来评估模型性能。同时,绘制实际值与预测值的关系图以便直观比较。
- 特征重要性:显示每个特征的重要性评分,帮助理解哪些特征对模型更重要。
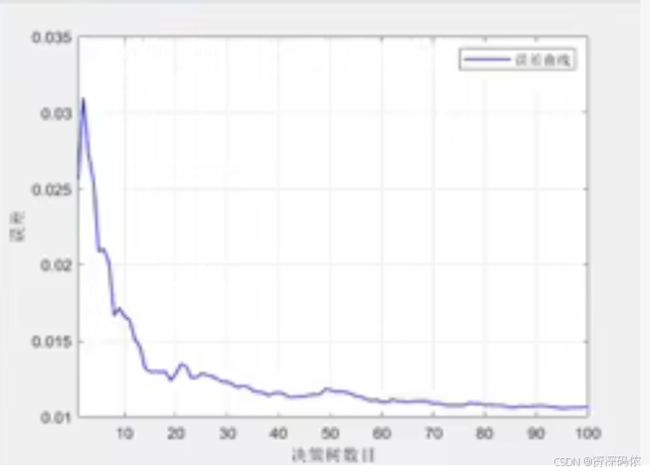
- 绘制误差曲线:绘制随着决策树数量增加时的误差变化曲线。
示例输出:
- 均方误差 (MSE):模型预测结果与实际值之间的误差。
- 散点图:实际值与预测值的对比图。
- 特征重要性:每个特征对模型预测的重要程度。
- 误差曲线:随着决策树数量增加时的误差变化曲线。