支持向量机(SVM)原理及公式推导
今天来看一下西瓜书第六章——支持向量机。
文章目录
-
-
- 定义
- 对偶问题
- 核函数
- 软间隔和正则化
- 支持向量回归
-
定义
SVM 就是一种二分类模型,他的基本模型是的定义在特征空间上的间隔(margin)最大的线性分类器,SVM 的学习策略就是找到间隔最大化的超平面。
我们来看这张图:
在这个二分类的图中,直觉告诉我们 H 3 H_3 H3 的泛化能力最好。对于 H 1 H_1 H1 来说,他不能把类别分开,这个分类器肯定是不行的。而 H 2 H_2 H2 可以,但是分割线与最近的数据点只有很小的间隔,一旦新数据有一定偏差,就会分类错误,也就是说他的泛化能力弱。
给定数据集:
D = { ( x 1 , y 1 ) , ⋯ , ( x m , y m ) } , y i ∈ { − 1 , + 1 } \begin{aligned} D=\left \{ (x_1,y_1),\cdots,(x_m,y_m) \right \},\text{ }y_i \in \left \{ -1,+1 \right \} \end{aligned} D={(x1,y1),⋯,(xm,ym)}, yi∈{−1,+1}
对于支持向量机来说,若数据点是 p p p 维向量,则可以用 p − 1 p-1 p−1 维的超平面来分开这些数据点。往往这样的超平面有很多,我们要找的就是最佳超平面,即以最大间隔把两个类分开的超平面。SVM 可以帮我们做到。
在样本空间中,划分超平面可通过如下线性方程来表示:
w T x + b = 0 w^Tx+b=0 wTx+b=0
其中 w = ( w 1 ; ⋯ ; w p ) w=(w_1;\cdots;w_p) w=(w1;⋯;wp) 为超平面的法向量, b b b 为偏移量。
样本空间中任意点到超平面的距离为:
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{|w^Tx+b|}{||w||} r=∣∣w∣∣∣wTx+b∣
其中 ∣ ∣ w ∣ ∣ = w 1 2 + ⋯ + w p 2 ||w||=\sqrt{w_1^2+\cdots+w_p^2} ∣∣w∣∣=w12+⋯+wp2
现在假设我们有 w T x + b = 0 w^Tx+b=0 wTx+b=0 该线性方程来划分两类数据,也就是说,当 y i = + 1 y_i=+1 yi=+1 时,有 w T x i + b > 0 w^Tx_i+b>0 wTxi+b>0;当 y i = − 1 y_i=-1 yi=−1 时,有 w T x i + b < 0 w^Tx_i+b<0 wTxi+b<0。
那我们想求得 margin 最大的分界线(两条线),现在令:
{ w T x i + b ≥ + 1 , y i = + 1 w T x i + b ≤ − 1 , y i = − 1 \begin{cases} w^Tx_i+b\ge+1,&y_i=+1\\\\ w^Tx_i+b\le-1,&y_i=-1 \end{cases} ⎩⎪⎨⎪⎧wTxi+b≥+1,wTxi+b≤−1,yi=+1yi=−1
于是可以得到: y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b)\ge 1 yi(wTxi+b)≥1,我们称为函数间隔。
为什么以 + − 1 +-1 +−1 来区分两类数据?原因是只要给定一个数 ξ \xi ξ,以 + − ξ +-\xi +−ξ 划分即可,只是改变了 w w w 和 b b b 而已,并不会影响求解的过程。
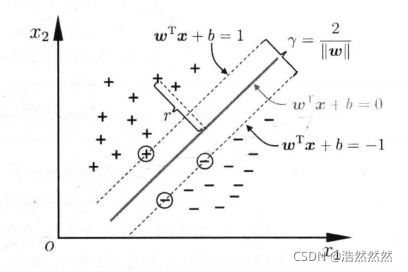
有了上述两条边界超平面后,我们称在边界上的点为支持向量,如下图所示。很显然,两个异类支持向量的间隔(margin)为:
γ = 2 ∣ ∣ w ∣ ∣ \gamma=\frac{2}{||w||} γ=∣∣w∣∣2
我们的目标是使 margin 最大,这样,模型的泛化能力更强。于是有:
max w , b 2 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \max_{w,b} \frac{2}{||w||}\\\\ s.t. \text{ } y_i(w^Tx_i+b)\ge1,i=1,2,\cdots,m w,bmax∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,⋯,m
为了方便求解,我们将上述目标重写一下,有:
min w , b ∣ ∣ w ∣ ∣ 2 2 s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \min_{w,b} \frac{||w||^2}{2}\\\\ s.t. \text{ } y_i(w^Tx_i+b)\ge1,i=1,2,\cdots,m w,bmin2∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,⋯,m
以上就是 SVM 损失函数的最初形态。
在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用。也就是说非支持向量的移动并不会影响最优超平面的产生。
对偶问题
我们希望通过上述的单目标规划求解得到参数 ( w , b ) (w,b) (w,b),虽然可以用优化包求解,但是考虑到对偶问题更易求解,由下文知对偶问题只需优化一个变量 α \alpha α 且约束条件更简单。且能更加自然地引入核函数,进而推广到非线性问题。
因此,我们用拉格朗日乘数法进行求解,首先构造拉格朗日函数,对 ∀ α i ≥ 0 \forall \alpha_i \ge 0 ∀αi≥0,有以下式子:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i (1-y_i(w^Tx_i+b)) L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
注意到当 1 − y i ( w T x i + b ) > 0 1-y_i(w^Tx_i+b)> 0 1−yi(wTxi+b)>0,即属于不可行解时,有:
max α L ( w , b , α ) = + ∞ \max_{\alpha} L(w,b,\alpha)=+\infty αmaxL(w,b,α)=+∞
最后是收敛不了的,也可以看到拉格朗日函数构造的巧妙。
而当 1 − y i ( w T x i + b ) ≤ 0 1-y_i(w^Tx_i+b)\le 0 1−yi(wTxi+b)≤0,即属于可行解时,有:
max α L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 \max_{\alpha} L(w,b,\alpha)=\frac{1}{2}||w||^2 αmaxL(w,b,α)=21∣∣w∣∣2
也就是说,下面两个问题是等价的。
min w , b max α L ( w , b , α ) ≡ min w , b ∣ ∣ w ∣ ∣ 2 2 \min_{w,b}\max_{\alpha} L(w,b,\alpha)\equiv \min_{w,b} \frac{||w||^2}{2} w,bminαmaxL(w,b,α)≡w,bmin2∣∣w∣∣2
根据拉格朗日对偶性,因为这里是强对偶问题(硬间隔问题),因此有:
max α min w , b L ( w , b , α ) ≡ min w , b max α L ( w , b , α ) ≡ min w , b ∣ ∣ w ∣ ∣ 2 2 \max_{\alpha}\min_{w,b} L(w,b,\alpha) \equiv \min_{w,b}\max_{\alpha} L(w,b,\alpha) \equiv \min_{w,b} \frac{||w||^2}{2} αmaxw,bminL(w,b,α)≡w,bminαmaxL(w,b,α)≡w,bmin2∣∣w∣∣2
令 ∂ L ( w , b , α ) ∂ w , ∂ L ( w , b , α ) ∂ b \frac{\partial L(w,b,\alpha)}{\partial w},\frac{\partial L(w,b,\alpha)}{\partial b} ∂w∂L(w,b,α),∂b∂L(w,b,α) 为 0 0 0。于是有:
{ w = ∑ i = 1 m α i y i x i 0 = ∑ i = 1 m α i y i \begin{cases} w=\sum_{i=1}^{m}\alpha_iy_ix_i\\\\ 0=\sum_{i=1}^{m}\alpha_iy_i \end{cases} ⎩⎪⎨⎪⎧w=∑i=1mαiyixi0=∑i=1mαiyi
将上述结果带入 max α min w , b L ( w , b , α ) \max_{\alpha}\min_{w,b} L(w,b,\alpha) maxαminw,bL(w,b,α) 后,有:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \max_\alpha \sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j x_i^T x_j αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
原问题的对偶问题为:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . { ∑ i = 1 m α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , m \begin{aligned} &\max_\alpha \sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j x_i^T x_j\\\\ &s.t. \begin{cases} \text{ } \sum_{i=1}^{m} \alpha_iy_i=0\\\\ \alpha_i\ge0,\text{ } i=1,2,\cdots,m \end{cases} \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t.⎩⎪⎨⎪⎧ ∑i=1mαiyi=0αi≥0, i=1,2,⋯,m
人们往往用序列最小优化(SMO)算法进行求解对偶问题。
假设已经求得未知数 α \alpha α,我们记为 α ^ \hat{\alpha} α^,就可以得出
w ^ = ∑ i = 1 m α ^ i y i x i \hat{w}=\sum_{i=1}^{m}\hat{\alpha}_iy_ix_i w^=i=1∑mα^iyixi
实际上,上述过程要满足 K K T KKT KKT 条件:
{ α i ≥ 0 y i ( w T x i + b ) − 1 ≥ 0 α i ( y i ( w T x i + b ) − 1 ) = 0 \begin{cases} \alpha_i\ge0\\\\ y_i(w^Tx_i+b)-1\ge0\\\\ \alpha_i(y_i(w^Tx_i+b)-1)=0 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧αi≥0yi(wTxi+b)−1≥0αi(yi(wTxi+b)−1)=0
当然,前两个条件是显然成立的。再来看第三个条件,有两种情况:
当 α i = 0 \alpha_i=0 αi=0,即该样本点不是支持向量,对模型没有作用。
当 y i ( w T x i + b ) − 1 = 0 y_i(w^Tx_i+b)-1=0 yi(wTxi+b)−1=0,即该样本点位于最大间隔边界上,是一个支持向量。
也应证了前面说的 SVM 只与支持向量有关,与非支持向量无关。
并且我们可以知道 ∃ α j > 0 \exists \alpha_j>0 ∃αj>0(若 ∀ α j = 0 \forall \alpha_j=0 ∀αj=0(都是非支持向量),那么 w = 0 w=0 w=0,即 max α L ( w , b , α ) = + ∞ \max_{\alpha} L(w,b,\alpha)=+\infty maxαL(w,b,α)=+∞,此时无解!!!),于是 ∃ j \exists j ∃j,使得 y j ( w T x j + b ) − 1 = 0 y_j(w^Tx_j+b)-1=0 yj(wTxj+b)−1=0(任意一个支持向量),此时,可以求得 b ^ \hat{b} b^,如下:
b ^ = 1 y j − w ^ T x j = 1 y j − ∑ i = 1 m α ^ i y i x i T x j \begin{aligned} \hat{b}&=\frac{1}{y_j}-\hat{w}^Tx_j\\ &=\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_iy_ix_i^Tx_j \end{aligned} b^=yj1−w^Txj=yj1−i=1∑mα^iyixiTxj
那么,我们求得的模型为:
f ( x ) = s i g n ( w ^ T x + b ^ ) = s i g n ( ∑ i = 1 m α ^ i y i x i T x + 1 y j − ∑ i = 1 m α ^ i y i x j T x i ) \begin{aligned} f(x)&=sign(\hat{w}^Tx+\hat{b})\\ &=sign(\sum_{i=1}^{m}\hat{\alpha}_iy_ix_i^Tx+\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_iy_ix_j^Tx_i) \end{aligned} f(x)=sign(w^Tx+b^)=sign(i=1∑mα^iyixiTx+yj1−i=1∑mα^iyixjTxi)
间隔最大超平面为:
∑ i = 1 m α ^ i y i x i T x + 1 y j − ∑ i = 1 m α ^ i y i x j T x i = 0 \sum_{i=1}^{m}\hat{\alpha}_iy_ix_i^Tx+\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_iy_ix_j^Tx_i=0 i=1∑mα^iyixiTx+yj1−i=1∑mα^iyixjTxi=0
核函数
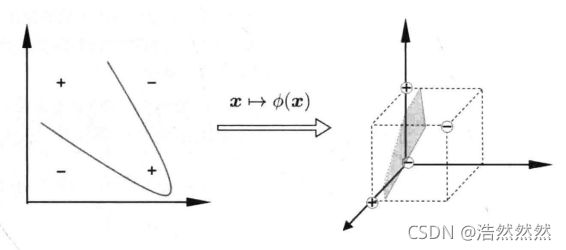
当数据不是线性可分的时候,如下图,我们需要将数据进行升维。
为了能够找出非线性数据的线性决策边界,我们需要将数据 x x x 非线性变换映射到高维空间 ϕ ( x ) \phi(x) ϕ(x) 中。 ϕ \phi ϕ 是一个映射函数,线性 SVM 的原理可以被很容易推广到非线性情况下,其推导过程和逻辑都与线性 SVM 一样,只不过在定义决策边界之前,我们必须先对数据进行升维度,即将原始的 x x x 转换成 ϕ ( x ) \phi(x) ϕ(x)。
和硬间隔的求解类似,模型为 f ( x ) = w T ϕ ( x ) + b f(x)=w^T\phi(x)+b f(x)=wTϕ(x)+b。
目标与约束如下:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T ϕ ( x i ) + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \min_{w,b} \text{ } \frac{1}{2}||w||^2\\\\ s.t. \text{ } y_i(w^T\phi(x_i)+b)\ge1 ,\text{ }i=1,2,\cdots,m w,bmin 21∣∣w∣∣2s.t. yi(wTϕ(xi)+b)≥1, i=1,2,⋯,m
其对偶问题为:
max a ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ T ( x i ) ϕ ( x j ) s . t . { ∑ i = 1 m α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , m \begin{aligned} &\max_a \sum_{i=1}^{m}\alpha_i -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j \phi^T(x_i)\phi(x_j)\\\\ &s.t. \begin{cases} \text{ } \sum_{i=1}^{m} \alpha_i y_i=0\\\\ \alpha_i\ge0,\text{ } i=1,2,\cdots,m \end{cases} \end{aligned} amaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕT(xi)ϕ(xj)s.t.⎩⎪⎨⎪⎧ ∑i=1mαiyi=0αi≥0, i=1,2,⋯,m
而考虑到映射高维空间的 ϕ T ( x i ) ϕ ( x j ) \phi^T(x_i)\phi(x_j) ϕT(xi)ϕ(xj) 作內积的计算比较困难,因此,设计一个核函数在原来的空间计算替换。
κ ( x i , x j ) = < ϕ ( x i ) , ϕ ( x j ) > = ϕ T ( x i ) ϕ ( x j ) \kappa(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi^T(x_i)\phi(x_j) κ(xi,xj)=<ϕ(xi),ϕ(xj)>=ϕT(xi)ϕ(xj)
那么对偶问题重写如下:
max a ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j κ ( x i , x j ) s . t . { ∑ i = 1 m α i y i = 0 α i ≥ 0 , i = 1 , 2 , ⋯ , m \begin{aligned} &\max_a \sum_{i=1}^{m}\alpha_i -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j \kappa(x_i,x_j)\\\\ &s.t. \begin{cases} \text{ } \sum_{i=1}^{m} \alpha_i y_i=0\\\\ \alpha_i\ge0,\text{ } i=1,2,\cdots,m \end{cases} \end{aligned} amaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)s.t.⎩⎪⎨⎪⎧ ∑i=1mαiyi=0αi≥0, i=1,2,⋯,m
求解得到模型为:
f ( x ) = s i g n ( w ^ T ϕ ( x ) + b ^ ) = s i g n ( ∑ i = 1 m α ^ i y i ϕ T ( x i ) ϕ ( x ) + 1 y j − ∑ i = 1 m α ^ i y i ϕ T ( x j ) ϕ ( x i ) ) = s i g n ( ∑ i = 1 m α ^ i y i κ ( x i , x ) + 1 y j − ∑ i = 1 m α ^ i y i κ ( x j , x i ) ) \begin{aligned} f(x)&=sign(\hat{w}^T\phi(x)+\hat{b})\\ &=sign(\sum_{i=1}^{m}\hat{\alpha}_i y_i \phi^T(x_i)\phi(x)+\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_i y_i \phi^T(x_j)\phi(x_i))\\ &=sign(\sum_{i=1}^{m}\hat{\alpha}_i y_i \kappa(x_i,x)+\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_i y_i \kappa(x_j,x_i)) \end{aligned} f(x)=sign(w^Tϕ(x)+b^)=sign(i=1∑mα^iyiϕT(xi)ϕ(x)+yj1−i=1∑mα^iyiϕT(xj)ϕ(xi))=sign(i=1∑mα^iyiκ(xi,x)+yj1−i=1∑mα^iyiκ(xj,xi))
间隔最大超平面为:
∑ i = 1 m α ^ i y i κ ( x i , x ) + b ^ ) + 1 y j − ∑ i = 1 m α ^ i y i κ ( x j , x i ) = 0 \sum_{i=1}^{m}\hat{\alpha}_i y_i \kappa(x_i,x)+\hat{b})+\frac{1}{y_j}-\sum_{i=1}^{m}\hat{\alpha}_i y_i \kappa(x_j,x_i)=0 i=1∑mα^iyiκ(xi,x)+b^)+yj1−i=1∑mα^iyiκ(xj,xi)=0
这里 κ ( ⋅ , ⋅ ) \kappa(·,·) κ(⋅,⋅) 是核函数。
常用的核函数如下:
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(x_i,x_j)=x_i^Tx_j κ(xi,xj)=xiTxj | |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(x_i,x_j)=(x_i^Tx_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d\ge1 d≥1为多项式的次数 |
| 高斯核 | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ 2 2 σ 2 ) \kappa(x_i,x_j)=\exp(-\frac{|x_i-x_j|^2}{2\sigma^2}) κ(xi,xj)=exp(−2σ2∣xi−xj∣2) | σ > 0 \sigma>0 σ>0为高斯核的带宽 |
| 拉普拉斯核 | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ 2 σ ) \kappa(x_i,x_j)=\exp(-\frac{ | x_i-x_j|^2}{\sigma}) κ(xi,xj)=exp(−σ∣xi−xj∣2) | σ > 0 \sigma>0 σ>0 |
| S i g m o i d Sigmoid Sigmoid核 | κ ( x i , x j ) = t a n h ( β x i T x j + θ ) \kappa(x_i,x_j)=tanh(\beta x_i^Tx_j+\theta) κ(xi,xj)=tanh(βxiTxj+θ) | t a n h tanh tanh为双曲正切函数, β > 0 \beta>0 β>0, θ < 0 \theta<0 θ<0 |
软间隔和正则化
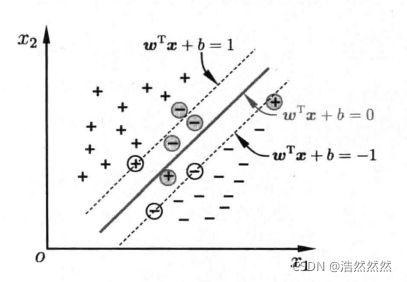
在前面介绍中,我们假定训练数据是严格线性可分的,即存在一个超平面能完全将两类数据分开。但是现实任务这个假设往往不成立,例如下图所示的数据。
那我们允许小部分数据不满足以下条件:
y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b)\ge1 yi(wTxi+b)≥1
为了使不满足上述条件的样本点尽可能少,我们需要在优化的目标函数新增一个对这些点的惩罚项。最常用的是 hinge 损失:
ℓ h i n g e ( z ) = m a x ( 0 , 1 − z ) \ell_{hinge}(z)=max(0,1-z) ℓhinge(z)=max(0,1−z)
即若样本点满足约束条件损失就是 0 0 0, 否则损失就是 1 − z 1-z 1−z,则优化目标为:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m m a x ( 0 , 1 − y i ( w T x i + b ) ) \min_{w,b} \text{ } \frac{1}{2}||w||^2+C\sum_{i=1}^{m}max(0,1-y_i(w^Tx_i+b)) w,bmin 21∣∣w∣∣2+Ci=1∑mmax(0,1−yi(wTxi+b))
其中 C C C 称为惩罚参数, C C C 越小时对误分类惩罚越小,越大时对误分类惩罚越大,当 C C C 取正无穷时就变成了硬间隔优化。实际应用时我们要合理选取 C C C, C C C 越小越容易欠拟合, C C C 越大越容易过拟合(margin越小)。
引入松弛变量 ξ i ≥ 0 \xi_i\ge0 ξi≥0,将目标重写为:
min w , b , ξ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i s . t . { y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 i = 1 , 2 , ⋯ , m \begin{aligned} &\min_{w,b,\xi_i} \text{ } \frac{1}{2}||w||^2+C\sum_{i=1}^{m}\xi_i\\\\ &s.t. \begin{cases} y_i(w^Tx_i+b)\ge1-\xi_i\\\\ \xi_i\ge0 \text{ } i=1,2,\cdots,m \end{cases} \end{aligned} w,b,ξimin 21∣∣w∣∣2+Ci=1∑mξis.t.⎩⎪⎨⎪⎧yi(wTxi+b)≥1−ξiξi≥0 i=1,2,⋯,m
与前面一样,通过拉格朗日乘数法进行求解,构造拉格朗日函数,对 ∀ α i ≥ 0 , μ i ≥ 0 \forall \alpha_i \ge 0, \mu_i\ge0 ∀αi≥0,μi≥0,有以下式子:
L ( w , b , α , ξ , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i L(w,b,\alpha,\xi,\mu)=\frac{1}{2}||w||^2+C\sum_{i=1}^{m}\xi_i+\sum_{i=1}^{m}\alpha_i(1-\xi_i-y_i(w^Tx_i+b))-\sum_{i=1}^{m}\mu_i\xi_i L(w,b,α,ξ,μ)=21∣∣w∣∣2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wTxi+b))−i=1∑mμiξi
令 ∂ L ( w , b , α , ξ , μ ) ∂ w , ∂ L ( w , b , α , ξ , μ ) ∂ b , ∂ L ( w , b , α , ξ , μ ) ∂ ξ i \frac{\partial L(w,b,\alpha,\xi,\mu)}{\partial w},\frac{\partial L(w,b,\alpha,\xi,\mu)}{\partial b},\frac{\partial L(w,b,\alpha,\xi,\mu)}{\partial \xi_i} ∂w∂L(w,b,α,ξ,μ),∂b∂L(w,b,α,ξ,μ),∂ξi∂L(w,b,α,ξ,μ) 为 0 0 0。于是有:
{ w = ∑ i = 1 m α i y i x i 0 = ∑ i = 1 m α i y i C = α i + μ i \begin{cases} w=\sum_{i=1}^{m}\alpha_iy_ix_i\\\\ 0=\sum_{i=1}^{m}\alpha_iy_i\\\\ C=\alpha_i+\mu_i \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧w=∑i=1mαiyixi0=∑i=1mαiyiC=αi+μi
将上述结果带入拉格朗日函数即可得到对偶问题为:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . { ∑ i = 1 m α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , ⋯ , m \begin{aligned} &\max_\alpha \text{ } \sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i \alpha_j y_i y_j x_i^Tx_j\\\\ &s.t. \begin{cases} \sum_{i=1}^{m}\alpha_iy_i=0\\\\ 0\le \alpha_i \le C,\text{ } i=1,2,\cdots,m \end{cases} \end{aligned} αmax i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t.⎩⎪⎨⎪⎧∑i=1mαiyi=00≤αi≤C, i=1,2,⋯,m
上述过程 K K T KKT KKT 条件为:
{ α i ≥ 0 , μ i ≥ 0 y i ( w T x i + b ) − 1 + ξ i ≥ 0 α i ( y i ( w T x i + b ) − 1 + ξ i ) = 0 ξ i ≥ 0 , μ i ξ i = 0 \begin{cases} \alpha_i \ge0,\mu_i \ge0\\\\ y_i(w^Tx_i+b)-1+\xi_i\ge0\\\\ \alpha_i(y_i(w^Tx_i+b)-1+\xi_i)=0\\\\ \xi_i \ge0,\mu_i\xi_i=0 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧αi≥0,μi≥0yi(wTxi+b)−1+ξi≥0αi(yi(wTxi+b)−1+ξi)=0ξi≥0,μiξi=0
与前面一样,用 SMO 求解即可。
支持向量回归
前面介绍完了分类,这里介绍回归问题,我们称为支持向量回归(SVR)。
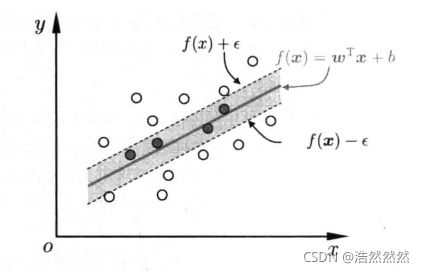
给定样本 D = { ( x 1 , y 1 ) , ⋯ , ( x m , y m ) } D=\left \{ (x_1,y_1),\cdots,(x_m,y_m) \right \} D={(x1,y1),⋯,(xm,ym)}, y i ∈ R y_i\in R yi∈R,我们希望学得一个回归模型,使 f ( x ) f(x) f(x) 与 y y y 尽可能接近。
SVR 假设 f ( x ) f(x) f(x) 与 y y y 最多有 ε \varepsilon ε 的偏差,这相当于以 f ( x ) f(x) f(x) 为中心,构建了一个宽度为 2 ε 2\varepsilon 2ε 的间隔带,若训练样本落入此间隔带,则认为是被预测正确的。
于是,SVR 问题为:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ℓ ε ( f ( x i ) − y i ) \min_{w,b} \text{ } \frac{1}{2}||w||^2+C\sum_{i=1}^{m}\ell_\varepsilon (f(x_i)-y_i) w,bmin 21∣∣w∣∣2+Ci=1∑mℓε(f(xi)−yi)
其中 C C C 为正则化常数, ℓ ε \ell_\varepsilon ℓε 为损失函数:
ℓ ε ( z ) { 0 , i f ∣ z ∣ ≤ ε ∣ z ∣ − ε , o t h e r w i s e \ell_\varepsilon(z) \begin{cases} 0, & if |z|\le \varepsilon\\\\ |z|-\varepsilon,&otherwise \end{cases} ℓε(z)⎩⎪⎨⎪⎧0,∣z∣−ε,if∣z∣≤εotherwise
引入松弛变量 ξ i \xi_i ξi 和 ξ ^ i \hat{\xi}_i ξ^i,可将原问题转化为:
min w , b , ξ i , ξ ^ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) s . t . { f ( x i ) − y i ≤ ε + ξ i y i − f ( x i ) ≤ ε + ξ ^ i ξ i ≥ 0 , ξ ^ i ≥ 0 , i = 1 , 2 , ⋯ , m \begin{aligned} &\min_{w,b,\xi_i,\hat{\xi}_i} \text{ } \frac{1}{2}||w||^2 + C\sum_{i=1}^{m}(\xi_i+\hat{\xi}_i)\\\\ &s.t. \begin{cases} f(x_i)-y_i\le \varepsilon+\xi_i\\\\ y_i-f(x_i)\le \varepsilon+\hat{\xi}_i\\\\ \xi_i \ge0,\hat{\xi}_i\ge0,\text{ } i=1,2,\cdots,m \end{cases} \end{aligned} w,b,ξi,ξ^imin 21∣∣w∣∣2+Ci=1∑m(ξi+ξ^i)s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧f(xi)−yi≤ε+ξiyi−f(xi)≤ε+ξ^iξi≥0,ξ^i≥0, i=1,2,⋯,m
类似的,设拉格朗日函数为:
L ( w , b , α , α ^ , ξ , ξ ^ , μ , μ ^ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) − ∑ i = 1 m μ i ξ i − ∑ i = 1 m μ ^ i ξ ^ i + ∑ i = 1 m α i ( f ( x i ) − y i − ε − ξ i ) + ∑ i = 1 m α ^ i ( y i − f ( x i ) − ε − ξ ^ i ) \begin{aligned} L(w,b,\alpha,\hat{\alpha},\xi,\hat{\xi},\mu,\hat{\mu})&=\frac{1}{2}||w||^2+C\sum_{i=1}^{m}(\xi_i+\hat{\xi}_i)-\sum_{i=1}^{m}\mu_i \xi_i-\sum_{i=1}^{m}\hat{\mu}_i\hat{\xi}_i\\\\ &+\sum_{i=1}^{m}\alpha_i(f(x_i)-y_i-\varepsilon-\xi_i)+\sum_{i=1}^{m}\hat{\alpha}_i(y_i-f(x_i)-\varepsilon-\hat{\xi}_i) \end{aligned} L(w,b,α,α^,ξ,ξ^,μ,μ^)=21∣∣w∣∣2+Ci=1∑m(ξi+ξ^i)−i=1∑mμiξi−i=1∑mμ^iξ^i+i=1∑mαi(f(xi)−yi−ε−ξi)+i=1∑mα^i(yi−f(xi)−ε−ξ^i)
对上述函数的 w , b , ξ i , ξ ^ i w,b,\xi_i,\hat{\xi}_i w,b,ξi,ξ^i 分别求偏导后,置为 0 0 0 得到:
{ w = ∑ i = 1 m ( α ^ i − α i ) x i 0 = ∑ i = 1 m ( α ^ i − α i ) C = α i + μ i C = α ^ i + μ ^ i \begin{cases} w=\sum_{i=1}^{m}(\hat{\alpha}_i-\alpha_i)x_i\\\\ 0=\sum_{i=1}^{m}(\hat{\alpha}_i-\alpha_i)\\\\ C=\alpha_i+\mu_i\\\\ C=\hat{\alpha}_i+\hat{\mu}_i \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧w=∑i=1m(α^i−αi)xi0=∑i=1m(α^i−αi)C=αi+μiC=α^i+μ^i
将上述结果带入拉格朗日函数,得到 SVR 对偶问题为:
max α , α ^ ∑ i = 1 m y i ( α ^ i − α i ) − ε ( α ^ i + α i ) − 1 2 ∑ i = 1 m ∑ j = 1 m ( α ^ i − α i ) ( α ^ j − α j ) x i T x j s . t . { ∑ i = 1 m ( α ^ i − α i ) = 0 0 ≤ α i , α ^ i ≤ C \begin{aligned} \max_{\alpha,\hat{\alpha}} \text{ } &\sum_{i=1}^{m}y_i(\hat{\alpha}_i-\alpha_i)-\varepsilon(\hat{\alpha}_i+\alpha_i)\\ &-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}(\hat{\alpha}_i-\alpha_i)(\hat{\alpha}_j-\alpha_j)x_i^Tx_j\\\\ &s.t. \begin{cases} \sum_{i=1}^{m}(\hat{\alpha}_i-\alpha_i)=0\\\\ 0\le \alpha_i,\hat{\alpha}_i \le C \end{cases} \end{aligned} α,α^max i=1∑myi(α^i−αi)−ε(α^i+αi)−21i=1∑mj=1∑m(α^i−αi)(α^j−αj)xiTxjs.t.⎩⎪⎨⎪⎧∑i=1m(α^i−αi)=00≤αi,α^i≤C
上述过程需满足 K K T KKT KKT 条件:
{ α i ( f ( x i ) − y i − ε − ξ i ) = 0 α ^ i ( y i − f ( x i ) − ε − ξ ^ i ) = 0 α i α ^ i = 0. ξ i ξ i ^ = 0 ( C − α i ) ξ i = 0 , ( C − α ^ i ξ ^ i ) = 0 \begin{cases} \alpha_i(f(x_i)-y_i-\varepsilon-\xi_i)=0\\\\ \hat{\alpha}_i(y_i-f(x_i)-\varepsilon-\hat{\xi}_i)=0\\\\ \alpha_i\hat{\alpha}_i=0.\xi_i\hat{\xi_i}=0\\\\ (C-\alpha_i)\xi_i=0,(C-\hat{\alpha}_i\hat{\xi}_i)=0 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧αi(f(xi)−yi−ε−ξi)=0α^i(yi−f(xi)−ε−ξ^i)=0αiα^i=0.ξiξi^=0(C−αi)ξi=0,(C−α^iξ^i)=0
前两个条件可以看出只要样本 ( x i , y i ) (x_i,y_i) (xi,yi) 落入 2 ε 2\varepsilon 2ε 的间隔带中(即 α i 或 α ^ i 可以取非零值 \alpha_i \text{或} \hat{\alpha}_i \text{可以取非零值} αi或α^i可以取非零值)
相应的,SVR 的解为:
f ( x ) = ∑ i = 1 m ( α ^ i − α i ) x i T x + b f(x)=\sum_{i=1}^{m}(\hat{\alpha}_i-\alpha_i)x_i^Tx+b f(x)=i=1∑m(α^i−αi)xiTx+b
而在第四个条件下,若得到了 α i \alpha_i αi,则 ξ i = 0 \xi_i=0 ξi=0,又有 0 < α i < C 0<\alpha_i
b = y i + ε − ∑ j = 1 m ( α ^ j − α j ) x j T x i b=y_i+\varepsilon-\sum_{j=1}^{m}(\hat{\alpha}_j -\alpha_j)x_j^Tx_i b=yi+ε−j=1∑m(α^j−αj)xjTxi
如果需要将原空间的数据 x x x 映射到 ϕ ( x ) \phi(x) ϕ(x) 的高维空间中,则模型为:
f ( x ) = ∑ i = 1 m ( α i ^ − α i ) κ ( x , x i ) + b f(x)=\sum_{i=1}^{m}(\hat{\alpha_i}-\alpha_i)\kappa(x,x_i)+b f(x)=i=1∑m(αi^−αi)κ(x,xi)+b
其中 κ ( x i , x j ) = ϕ T ( x i ) ϕ ( x j ) \kappa(x_i,x_j)=\phi^T(x_i)\phi(x_j) κ(xi,xj)=ϕT(xi)ϕ(xj) 为核函数。
那么,以上就是 SVM 和 SVR 的原理部分了,这个模型对二分类来说还是不错的。刚接触该模型确实还是有点难的,需要时间慢慢去磨。
参考资料
[1] 周志华.机器学习[M].北京:清华大学出版社,2020.