傅里叶变换的Python实现 自学笔记(二)画图篇 离散傅里叶变换DFT 零基础入门(最详细的从Python的角度而非数学角度了解傅里叶变换)
关键词:复数正弦波,离散傅里叶变换
概述
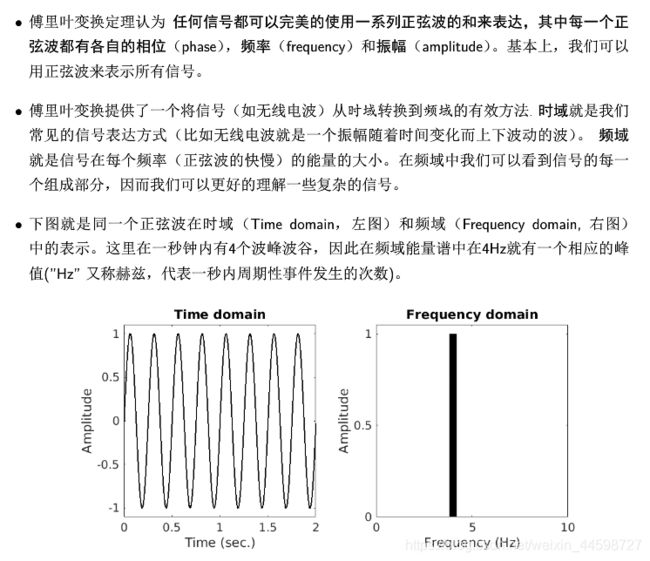
傅里叶变换,是把信号从时间域变换到频率域,进而研究信号的频谱结构和变化规律。上一篇文章中,我们讨论了Python、正弦波、复数。本篇文章中,我们继续用Python中的numpy+matplotlab的方式来实现复数正弦波和离散傅里叶变换。
注:我一共写3篇文章,去学习/记录 傅里叶变换的Python实现,提供一部分Python代码和一些数学上的思维过程,这是第二篇文章。
- (一)准备篇 Python和数学基础
- (二)画图篇 傅里叶变换 DFT
- (三)进阶篇 快速傅里叶变换 FFT
复数正弦波
正弦波的参数:振幅 频率 相位,但是如果我们在实数范围内(普通的正弦波)做傅里叶变换,一点点相位的偏差就会导致傅里叶变换结果较大的波动,但实际上这种波动是没有意义的,因此我们需要在复数范围内去做傅里叶变换。
我们前面曾谈到,欧拉公式将复数与三角函数联系起来,也就是说,我们可以提出这样一个想法:正弦波+欧拉公式=复数正弦波
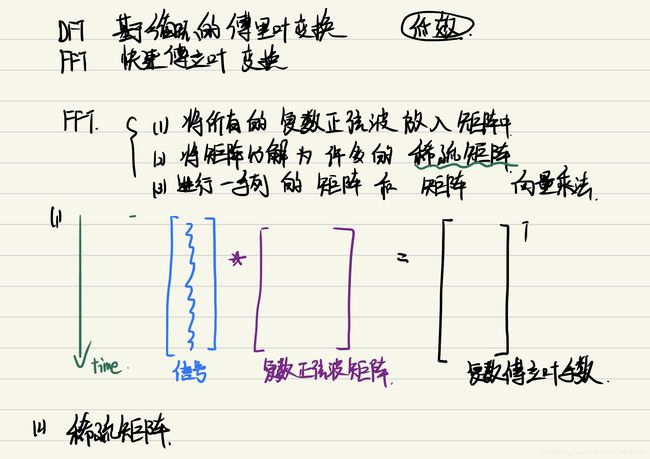
下面我附上了一些笔记,来展示这种转换的思维过程:

我们会发现,复数正弦波有3个维度,时间、正弦、余弦相关,我们一点点去理解他。
1.平面角度复数正弦波
首先,我们import相关的库
import numpy as np
import math
import matplotlib.pyplot as plt
接着,我们要设置一些参数,这里是构造一个离散的时间序列,序列越密集,就越接近数学意义上连续的时间轴(这部分是电脑用离散的点,模拟连续的波,可以不必理解)
# general simulation parameters
srate = 500; # sampling rate in Hz
time = np.arange(0.,2.,1./srate) # time in seconds
接下来,我们给出相应的正弦波的参数
# sine wave parameters
#正弦波:asin(2πft+θ) 参数:频率/相位/能量
freq = 5; # frequency in Hz
ampl = 2; # amplitude in a.u.
phas = np.pi/3; # phase in radians
然后,我们在平面中把他画出来
注意,这里并非是在复平面内画图,复数正弦波是3维的
这里面我们还是从频率-时间的角度去展现他
# generate the sine wave
csw = ampl * np.exp( 1j* (2*np.pi * freq * time + phas) )
# plot the results
plt.plot(time,np.real(csw),label='real')
plt.plot(time,np.imag(csw),label='imag')
最后,我们还是做一些画图的完善工作
plt.xlabel('Time (sec.)'), plt.ylabel('Amplitude')
plt.title('Complex sine wave projections')
plt.legend()
plt.show()
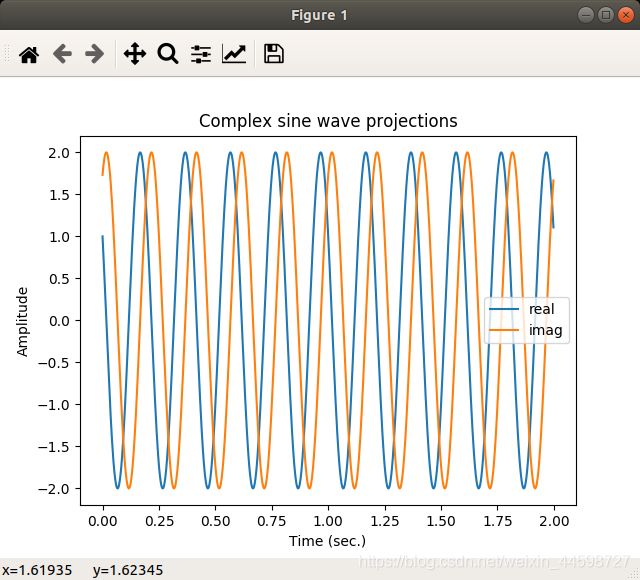
复数正弦波就展示出来来了,但是这个图有种“照骗”的感觉,
因为我们画出的是复数正弦波的实数部分(sin-wave)和虚数部分(cos—wave),而实际上这两部分在3维中应该是相互垂直的,imag轴和real轴。
2.三维角度复数正弦波
下面我们从3维角度来看看复数正弦波,由于代码比较趋同,我们不详细介绍。
我们先import相应的库,这次要用3D画图
import numpy as np
import math
import matplotlib.pyplot as plt
import pylab as pl
from mpl_toolkits.mplot3d import Axes3D
我们来给出相应的参数,模拟正弦波
# general simulation parameters
srate = 500; # sampling rate in Hz
time = np.arange(0.,2.,1./srate) # time in seconds
# sine wave parameters
freq = 5; # frequency in Hz
ampl = 2; # amplitude in a.u.
phas = np.pi/3; # phase in radians
# generate the sine wave
csw = ampl * np.exp( 1j* (2*np.pi * freq * time + phas) )
我们用3D的方法把复数正弦波展示出来
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(time,np.real(csw),np.imag(csw))
ax.set_xlabel('Time (s)'), ax.set_ylabel('Real part'), ax.set_zlabel('Imag part')
ax.set_title('Complex sine wave in all its 3D glory')
plt.show()
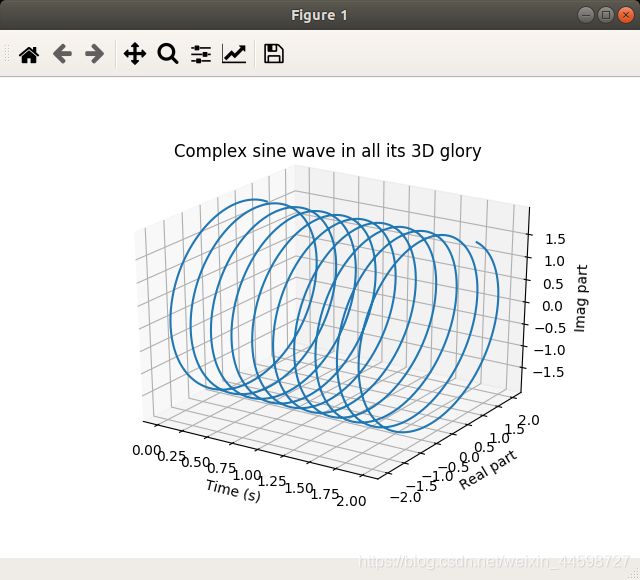
这次生成的是一个可以拖动的3D图像
如果我们在复平面内去看待他:
他会变成一个圆,与我们再讨论欧拉公式时的结论相符(无论k值如何变换,它的结果必然在一个圆上)。
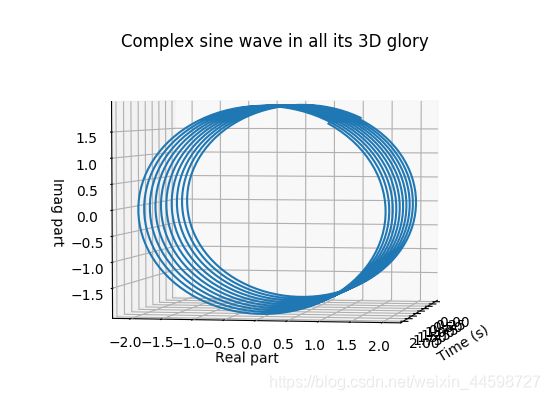
如果说我们从虚数-时间的角度去看待它:
我们会发现它长得越来越像一个标准正弦波,因为此时我们只看到了复数正弦波的虚数部分。
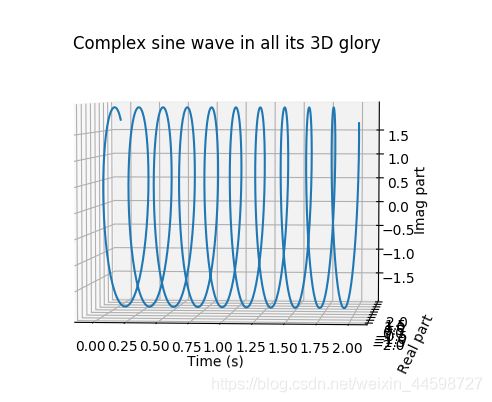
我们可以在Python画出的图像中,通过拖动图像以多个角度来看待复数正弦波,可以再修改一些参数,我们就能够比较准确的理解复数正弦波了~
注:Matplotlab的函数参数可以有很多,换言之可以重载,你可以去增加颜色等等参数画出更看的图像。
离散型傅里叶变换
有了前面的数学基础,我们终于说到了正题,离散型傅里叶变换(DFT,Discrete Fourier Transform),或者叫“基于循环的傅里叶变换”。
我们还记得:傅里叶变换:时域信号转换为频域信号。
下面,我们开始算法的核心内容(这里看不懂可以多看下,或是用代码自己实现一下)。
首先,对于每个时间点的循环开始:
我们创建了一个与信号时间长度一样的复数正弦波,(频率由信号点个数-1),然后,我们计算(这些不同频率的)复数正弦波和(原始)信号的点积,这个点积的结果就是(我们要的)傅里叶系数。
对于信号,我们得到了结果(不懂这句话的可以看上图):
- 信号-振幅:傅里叶系数的赋值
- 信号-相位:傅里叶系数的角度
到此,基于循环的傅里叶变换就算说完了~
我们到Python中,去看看代码和图像,再去理解一遍。
(我是一条分割线)
首先,我们引入相关的库
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.fftpack
然后,我们去认为的创建一个叠加的信号
我们可以看出来,我们给出的模拟信号,是由两个信号叠加而来
- 频率=4hz,振幅=2.5
- 频率=6.5hz,振幅=1.5
由于信号使我们自己模拟的,也就是已知的.因此,我们可以用来检测我们一会要做的傅里叶变换结果的正确性。
# create the signal
srate = 1000 #hz
time = np.arange(0.,2.,1/srate) #time vector in seconds
#arange(start,end,step),生成一个数列,步长可以为小数
pnts = len(time) # number of time points
# len返回的是time序列的长度
# 给定的模拟信号
signal = 2.5 * np.sin( 2*np.pi*4*time ) + 1.5 * np.sin( 2*np.pi*6.5*time )
然后,我们再做一些准备工作
- fourTime,可以理解为 傅里叶变换的时间向量(序列)
- fCoefs,获取到的是一个长度为len(),用0填充的数组
意义:存储的是新的函数内容,即后续点积的结果
注:这两个变量的类型都是numpy库中的ndarry,这是一种非常好用和常用的数据结构,可以学习一个。
# prepare the Fourier transform
fourTime = np.array(range(0,pnts))/pnts
fCoefs = np.zeros((len(signal)),dtype=complex)
我们开始创建循环,和在循环中创建复数正弦波
然后,我们在循环中,计算复数正弦波与原来信号(模拟信号)的点积
点积的结果,其实就是各个频率的傅里叶系数
注:这里的点积也可以用np中的dot()函数
for fi in range(0,pnts):
# create complex sine wave
# 创建一个复数正弦波
# 创建不同频率的复数正弦波,fi是频率
csw = np.exp( -1j*2*np.pi*fi*fourTime )
# compute dot product between sine wave and signal
# these are called the Fourier coefficients
# 计算复数正弦波与原来信号(模拟信号)的点积
# 点积的结果,其实就是各个频率的傅里叶系数
fCoefs[fi] = np.sum( np.multiply(signal,csw) ) / pnts
然后,我们需要对数据进行一些处理
这里,需要了解什么是“奈奎斯特频率”和两个“正规化因子”。
篇幅所限,在此不多介绍。实际上,由时域信号转换为频域信号已经完成。
注:你可以理解为我们在变换过程中对原始信号进行了“一种处理”,我们必须反处理回去,才能在所有情况下,保证变换的没有任何问题。
# extract amplitudes
# 提取幅值×2,并取绝对值
ampls = 2*np.abs(fCoefs)
我们获取频率的序列,因为我们最后要画出频率-振幅 图像。
# compute frequencies vector
hz = np.linspace(0,srate/2,num=math.floor(pnts/2.)+1)
最后,我们画出傅里叶变换的结果,信号在频域中的样子。
注:这里,可能我们会产生疑问,为什么用stem函数而不是原来的plot函数?
实际上这两个函数用法非常类似,参数也近乎相同。不同点是
- plot函数,主要画连续的图,会自动把所有的点连成线(比如我们之前画的,许多点组成的(近乎连续的)sin函数)
- stem函数,本身意思就是“茎,柄”,画的是离散的图
# 画出傅里叶变换的结果
# 信号在频域中的样子
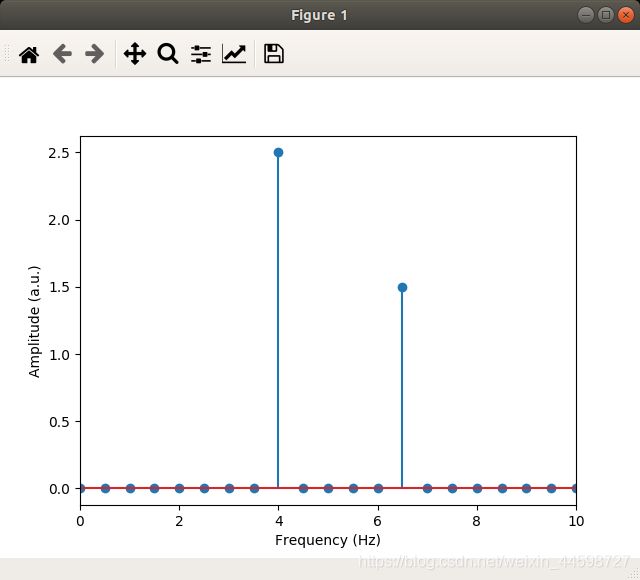
plt.stem(hz,ampls[range(0,len(hz))])
plt.xlabel('Frequency (Hz)'), plt.ylabel('Amplitude (a.u.)')
plt.xlim(0,10)
plt.show()
大功告成,我们可以从图片的结果中,看到这就是我们要的频域信号。
也正如我们前面所言,由于信号是模拟的,我们可以验证变换的正确性。我们也可以把模拟信号(两个正弦波)以时域信号的形式画出来再比较一下。
最后的话
1.FFT快速傅里叶变换
我们在本篇文章中讨论并且实现了离散型傅里叶变换DFT,让我们对于傅里叶变换有了进一步的认识。
但是,这种基于循环的傅里叶变换,尽管逻辑清晰,面对大量的数据是力不从心的。我们实际使用,往往用的是FFT,快速傅里叶变换,以稀疏矩阵为主要的数据结构,时间空间都更加合理。我们将在下一篇文章中去讨论和学习。
文章中的大部分内容,都是我一点点敲出来的,所有的代码,只要放在一起就可以在Python环境中运行。
关于傅里叶变换,我也是一位初学者,希望我的文章对大家能够有所参考。如果你看到我的文章以后,有任何指教或喜欢我写的文章,欢迎在下面评论或是联系我。
俗话说,有钱的捧个钱场,没钱的捧个人场~
再聊一点私货,这应该是CSDN上讲傅里叶变换,少有的舍弃数学公式,以Python和理解为主,数学知识比较简明的讨论。