逆转ISP，港科大陈启峰团队提出了可逆ISP

编辑：Happy
首发：AIWalker

Paper:https://arxiv.org/abs/2103.15061

code:https://github.com/yzxing87/Invertible-ISP

本文是港科大陈启峰老师团队在ISP方面的工作，已中CVPR2021。针对传统ISP中的信息损失且难以从sRGB进行RAW数据重建的问题，我们设计了一种可逆图像信号处理方案(InvISP)，它对RGB渲染与RAW重建进行联合优化。受益于所提方案的可逆性，我们可以直接从sRGB数据重建真实RAW数据且不会造成额外内存开销。所提方法对于raw数据压缩、retouch以及HDR等任务均有非常好的辅助作用。

Abstract

对于图像编辑与计算机视觉而言，未经处理的RAW数据是一种具有高度价值的图像格式。然而，由于RAW数据会导致保存的文件过大，用户往往只能获得处理并压缩后的sRGB图像。

为填补这一空缺，我们设计了一种可逆ISP(Invertible Image Signal Processing)方案，它可以进行sRGB图像的渲染，同时可以复原近乎完美的RAW数据。受益于所提框架的可逆性，我们可以从sRGB数据重建真实RAW数据，而非合成，且不会导致任何额外内存开销。与此同时，我们还集成了可谓分JPEG压缩模拟器，这使得所提框架可以直接从JPEG图像重建RAW数据。

在两个数码相机上的定量与定性实验表明：相比其他，本文所提方法可以得到具有更高质量的sRGB图像与重建RAW数据。

上图给出了本文所设计的可逆ISP流程示意图以及潜在应用场景。本文的主要贡献有这样几点：

• 首个从可逆ISP角度出发进行RAW数据重建的方案；
• 解决了ISP模块中的信息损失问题，且对JPEG压缩鲁棒；
• 在两个数码相机数据上验证了所提方案的有效性，并在多个应用场景(比如retouch、HDR等)验证了其潜在应用价值。

Traditional ISP Analysis

在正式介绍本文方案之前，我们先来看一下传统ISP对于RAW数据重建存在的挑战。现代数码相机通过ISP(它由一系列操作构成，包含白平衡、去马赛克、降噪、颜色空间转换、色调映射等)将RAW数据渲染为人眼可感知的RGB图像。传统ISP中的每一步都需要针对特定相机进行微调，这使得逆转传统ISP极具挑战。

接下来，我们将对传统ISP中存在信息损失的模块进行分析，并针对对性的进行重设计ISP使其成为一种端到端可逆ISP。

• Quantization & Tone Mapping。ISP的某些步骤(如去马赛克、gamma压缩)包含浮点操作，因此量化对于将数据转换到整数空间非常重要。比如，round操作理论上会带来$(-0.5,0.5)$的灰度误差。然而，tone mapping会进一步放大该灰度误差，上图给出了tonemapping曲线示意图。对于14-bit的raw数据，gamma压缩会使得$[16313,16383]$范围的数据压缩到255灰度，该步骤会导致单像素0.004RMSE误差。因此，直接从8-bit的sRGB数据合成14-bit的RAW数据极具挑战；
• Out-range Value Clipping。数值截断是一种常用的将raw数值规范化到合理范围的操作，常见于色彩空间转换、去马赛克、降噪、tone mapping等操作。传统ISP需要独立的进行手动调节，导致了误差累积，进一步加剧了信息损失。
• JPEG Compression。现代数码相机往往将RGB图像保存为JPEG格式，这会进一步加剧RAW图像重建的难度。JPEG包含四个步骤：颜色空间转换、离散余弦变换、量化、熵编码。事实上，量化是JPEG仅有的存在损失且非可微分的步骤。由于JPEG信息损失难以逆转，我们采用了一种“妥协”方式：将JPEG压缩步骤集成到所提框架中以消除信息损失。

Invertible Image Signal Processing

我们的目标是：设计一种可逆、双摄函数$f:\mathcal{X}\to \mathcal{Y}$用于RAW数据空间与sRGB数据空间之间的映射。我们假设RAW数据空间为$\mathcal{X}$，sRGB数据空间为$\mathcal{Y}$。为达到上述目的，经典神经网络需要两个独立网络近似$\mathcal{X}\to \mathcal{Y}$与$\mathcal{Y}\to \mathcal{X}$，这会导致不精确的双摄映射。

我们从另一个角度出发，采用仿射耦合层(affine coupling layers)使得单个网络可以进行双向映射。也就是说：我们采用多个可逆双摄函数$\{f_i{\}}_{i=0}^k$构成了所提可逆ISP。对于观测数据x，我们可以得到目标数据y：
$$\begin{gathered} y=f_0\circ f_1\circ f_2\circ \cdots \circ f_k(x) \\ x=f_k^{-1}\circ f_{k-1}^{-1}\circ \cdots \circ f_0^{-1}(y) \end{gathered}$$
每个$f_i$通过仿射耦合层实现，对于每个仿射耦合层，给定D维输入$\mathbf{m}$与$d<D$，输出$\mathbf{n}$计算方式如下：
$$\begin{gathered} {\mathbf{n}}_{1:d}={\mathbf{m}}_{1:d} \\ {\mathbf{n}}_{d+1:D}={\mathbf{m}}_{d+1:D}\odot exp(s({\mathbf{m}}_{1:d}))+t({\mathbf{m}}_{1:d}) \end{gathered}$$
其中，$s,t$表示$R^d\mapsto D^{D-d}$的尺度与变换函数。由于两者没必要可逆，故而我们通过神经网络进行实现。正如已有研究提到：耦合层遗留某些输入通道保持不变会限制了整个架构的表达能力。为缓解该问题，我们通过如下方式对耦合层增强：
$${\mathbf{n}}_{1:d}={\mathbf{m}}_{1:d}+r({\mathbf{m}}_{d+1:D})$$
逆转操作可以轻易得到，描述如下：
$$\begin{gathered} {\mathbf{m}}_{d+1:D}=({\mathbf{n}}_{d+1:D}-t({\mathbf{n}}_{1:d}))\odot exp(-s({\mathbf{n}}_{1:d})) \\ {\mathbf{m}}_{1:d}={\mathbf{n}}_{1:d}-r({\mathbf{m}}_{d+1:D}) \end{gathered}$$
接下来，我们采用可逆$1\times 1$卷积作为可学习置换函数为下一个仿射耦合层逆转通道顺序。

对于本文的image-to-image转换任务，我们直接学习RAW-to-RGB映射，无需对隐分布进行显示建模以稳定训练。考虑到可逆神经网络的输入与输出分辨率应当相同，我们采用去马赛克后RAW数据的双线性插值作为输入，这不会破坏RAW数据质量。

InvISP的前向过程生成sRGB图像，反向过程则旨在重建RAW数据。我们采用$L_1$损失进行双向训练：
$$L=\Vert f(x)-y{\Vert }_1+\lambda \Vert f^{-1}(y)-x{\Vert }_1$$

Differentiable JPEG Simulator

我们的目标是：训练一个鲁棒的可逆ISP，它可以容忍JPEG压缩导致的失真并重建精确的RAW数据。然而JPEG压缩算法是不可微分的，无法直接集成到前述所提端到端方案中。因此，我们提出一种可微分JPEG模拟器以使得所提方案与JPEG压缩鲁棒。

由于JPEG中的熵编码是无损的且位于量化之后，因此我们直接跳过该步骤仅仅模拟色彩空间变换、DCT以及量化三个步骤。为模拟DCT过程，我们计算DCT系数并将输入拆分为$8\times 8$块，每个块乘以DCT系数得到DCT特征图。在JPEG压缩中，所提DCT图由量化表拆分并round到整数类型。由于round函数不可微分，故而我们基于傅里叶变换设计了一种可微分版round函数，描述如下：
$$Q(I)=I-\frac{1}{\pi }\sum _{k=1}^K\frac{(-1{)}^{k+1}}{k}sin(2\pi kI)$$

随着K的增大，上述模拟函数会逐渐逼近真实round函数，但运行时间也会同样提升。上图给出了K=10时的round过程示意图。

Experiments

数据集方面：我们从MIT-Adobe FiveK中收集Canon EOS5D(777对)与Nikon D700(590对)子集制作训练与测试数据。我们对每个相机的数据按照$85:15$比例进行划分；采用LibRaw库处理Raw数据得到sRGB图像；JPEG压缩方面，质量设为90.

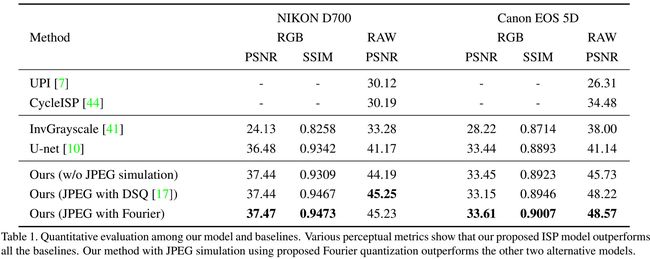
上表从定量角度对比了所提方法与UPI、CycleISP等方法的性能对比。可以看到：

• 相比UPI与CycleISP，所提方法可以重建更精确的RAW数据(PSNR甚至可以高出15dB)。这个结果并不惊讶：因为ISP中的信息损失是非常难以逆转的，这会导致比较差的合成Raw重加结果；而InvISP可以同时进行RGB与RAW重建优化。可以更好的处理量化、JPEG压缩以及数值截断等导致的信息损失。
• 相比InvGrayScale与UNet基线模型，所提方法同样具有更好的结果，这意味InvISP提供了一个更强的RAW数据重建方案。

上图从定性角度对比了所提方法与UPI、CycleISP的可视化效果对比。可以看到：本文所提InvISP可以更好的重建RAW数据，甚至在高光区域都能很好重建。

上图从定性角度对比了所提方法与InvGrayscale、UNet的可视化效果。可以看到：InvGrayscale难以在RGB与RAW之间取得比较好的均衡；而Unet可以取得比较的RGB结果，但在RAW重建方面表现较差；本文所提方法可以重建高质量的RAW数据且不会牺牲RGB性能。

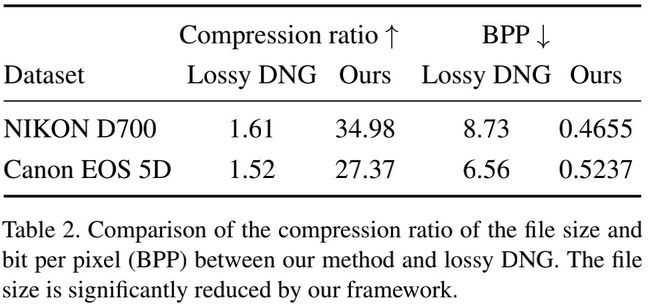
上表给出了所提方法在RAW数据压缩方面的性能对比。可以看到：相比有损DNG，所提方法可以进行更高比例的压缩。

上图给出了本文所提方法在retouch与HDR方面的应用效果。从中可以看到：

• 重建RAW数据与相机拍摄的RAW具有无法区分的视觉质量；
• 所提方法可以消除HDR过程中的过曝区域&欠曝区域的信息损失问题，进而取得更好的HDR重建结果。

推荐阅读

1. 你的感知损失可能用错了，沈春华团队提出随机权值广义感知损失
2. CVPR2021|超分性能不变，计算量降低50%，董超等人提出用于low-level加速的ClassSR
3. SANet|融合空域与通道注意力，南京大学提出置换注意力机制
4. GhostSR|针对图像超分的特征冗余，华为诺亚&北大联合提出GhostSR
5. 图像超分中的那些知识蒸馏
6. ICLR2021 | 显著提升小模型性能，亚利桑那州立大学&微软联合提出SEED
7. RepVGG|让你的ConVNet一卷到底，plain网络首次超过80%top1精度
8. Transformer再下一城！low-level多个任务榜首被占领
9. 通道注意力新突破！从频域角度出发，浙大提出FcaNet
10. 无需额外数据、Tricks、架构调整，CMU开源首个将ResNet50精度提升至80%+新方法
11. 46FPS+1080Px2超分+手机NPU，arm提出一种基于重参数化思想的超高效图像超分方案
12. 动态卷积超进化！通道融合替换注意力，减少75%参数量且性能显著提升 ICLR 2021
13. CVPR2021|“无痛涨点”的ACNet再进化，清华大学&旷视科技提出Inception类型的DBB