【论文笔记】Deep Learning on Graphs: A Survey
笔者:
- 此文章为笔者对于论文《Deep Learning on Graphs: A Survey》的一些译文和自己的一些看法
论文地址
1 INTRODUCTION
This problem is non-trivial because several challenges exist in applying traditional deep learning architectures to graphs:
这个问题是非常重要的,因为在将传统的深度学习架构应用于图形时存在一些挑战:
- Irregular structures of graphs.图的不规则结构
- Heterogeneity and diversity of graphs.图的异构性和多样性
- Large-scale graphs. 图过大
- Incorporating interdisciplinary knowledge.结合跨学科知识
We divide the existing methods into five categories based on their model architectures and training strategies:
我们根据模型架构和训练策略将现有方法分为五类:
-
Graph RNNs(graph recurrent neural networks) capture recursive and sequential patterns of graphs by modeling states at either the node-level or the graph-level.
图RNN图递归神经网络 通过在节点级或图级对状态进行建模来捕获图的递归和顺序模式。 -
GCNs(graph convolutional networks) defifine convolution and readout operations on irregular graph structures to capture common local and global structural patterns.
GCNs图卷积网络在不规则图形结构上定义了卷积和读出操作,以捕捉常见的局部和全局结构模式。 -
GAEs(graph autoencoders) assume low-rank graph structures and adopt unsupervised methods for node representation learning.
GAEs图自动编码采用低秩图结构,采用无监督的方法进行节点表示学习。 -
Graph RL(graph reinforcement learning) defifines graph-based actions and rewards to obtain feedbacks on graph tasks while following constraints.
Graph-RL图强化学习定义了基于图的行为和奖励,以获得对图任务的反馈,同时遵循约束条件。 -
Graph adversarial methods adopt adversarial training techniques to enhance the generalization ability of graph based models and test their robustness by adversarial attacks.
图对抗方法采用对抗性训练技术来提高基于图的模型的泛化能力,并通过对抗性攻击来检验其鲁棒性。
笔者:
- 由于图网络的结构等问题,将传统的深度学习方法应用于图是困难的。
- 图网络可大致分为5类,
Graph RNNs(graph recurrent neural networks)
GCNs(graph convolutional networks)
GAEs(graph autoencoders)
Graph RL(graph reinforcement learning)
Graph adversarial
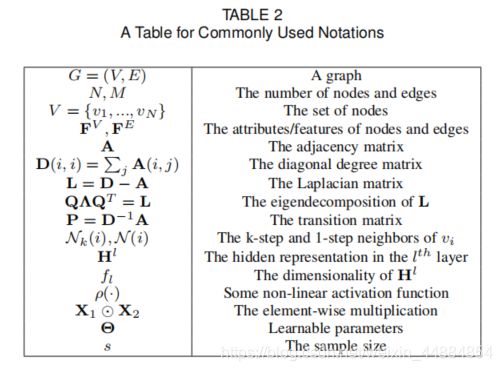
2.NOTATIONS AND PRELIMINARIES符号和准备
The tasks for learning a deep model on graphs can be broadly divided into two categories:
图深度学习任务大致可以分为两类:
- Node-focused tasks: These tasks are associated with individual nodes in the graph. Examples include node classifification, link prediction, and node recommendation.
图节点关注任务:示例包括节点分类、链路预测和节点推荐。 - Graph-focused tasks: These tasks are associated with the entire graph. Examples include graph classifification, estimating various graph properties, and generating graphs.
图关注任务:示例包括图形分类、估计各种图形属性和生成图形。
笔者:
- NOTATIONS为论文中的标注符号
- 图任务可以分为两类:
Node-focused tasks
Graph-focused tasks
3.GRAPH RECURRENT NEURAL NETWORKS
Recurrent neural networks (RNNs) such as gated recurrent units (GRU) [30] or long short-term memory (LSTM) [31] are defacto standards in modeling sequential data.
递归神经网络(RNN)如门控递归单元(GRU)[30]或长短期记忆(LSTM)[31]是序列数据建模的事实标准。
We review Graph RNNs which can capture recursive and sequential patterns of graphs.
我们回顾了可以捕获图的递归模式和序列模式的图RNNs。
Graph RNNs can be broadly divided into two categories: node-level RNNs and graph-level RNNs. The main distinction lies in whether the patterns lie at the node-level and are modeled by node states, or at the graph-level and are modeled by a common graph state.
图rnn大致可分为两类:节点级rnn和图级rnn。主要的区别在于模式是节点级RNNs由节点状态建模,还是在图级RNNs由一个公共的图状态建模。
笔者:
Graph RNNs的基础是LSTM和GRU
Graph RNNs大致可以分为两类:graph-level RNNs、node-level RNNs
下文详细解释了两种网络
3.1 Node-level RNNs
For graph-focused tasks, the authors of [23] suggested adding a special node with unique attributes to represent the entire graph.
对于以图为中心的任务,[23]的作者建议添加一个具有唯一属性的特殊节点来表示整个图形。
![]()
Although they are conceptually important, GNNs have several drawbacks.
虽然它们在概念上很重要,但是GNNs有几个缺点。
First,to ensure that Eq. (1) has a unique solution, F(·) must be a “contraction map”
为了确保等式(1)有唯一解,F(·)必须是“收缩图”.
Second, because many iterations are needed to reach a stable state between gradient descend steps, GNNs are computationally expensive.
因为在梯度下降需要很多次迭代才能达到稳定状态中,GNNs 在计算上很贵。
![]()
A notable improvement to GNNs is gated graph sequence neural networks (GGS-NNs) [24] with the following modifications.
GNNs的一个显著改进是选通图序列神经网络(GGS-NNs)[24],但有以下修改.
Most importantly, the authors replaced the recursive defifinition in Eq. (1) with a GRU, thus removing the “contraction map” requirement and supporting modern optimization techniques.
最重要的是,作者用GRU替换了公式(1)中的递归定义,从而消除了“收缩图”的要求,并支持现代优化技术。
![]()
SSE [25] took a similar approach as Eq.(4). However, instead of using a GRU in the calculation, SSE adopted stochastic fifixed point gradient descent to accelerate the training process.
SSE[25]采用了类似于公式(4)的方法。然而,在计算过程中,SSE没有使用GRU,而是采用随机五定点梯度下降来加速训练过程。
This scheme basically alternates between calculating steady node states using local neighborhoods and optimizing the model parameters, with both calculations in stochastic mini-batches.
该方案基本上交替使用局部邻域计算稳态节点状态和优化模型参数,两种计算都是随机小批量进行的。
笔者:
1.传统Graph RNNs要求图必须为“contraction map”(收敛图)
即:

2.GGS-NNs使用GRU让传统Graph RNNs消除了必须为“收敛图”的性质,并且支持了现代的优化技术
3.SSE 则采用类似于GGS-NNs的方法,没有用GRU,而是使用随机五定点梯度下降训练。
3.2 Graph-level RNNs
You et al. [26] applied Graph RNNs to the graph generation problem. Specififically, they adopted two RNNs: one to generate new nodes and the other to generate edges for the newly added node in an autoregressive manner.
…等。[26]将图RNNs应用于图生成问题。具体来说,他们采用了两个rnn:一个用于生成新节点,另一个用于以自回归方式为新添加的节点生成边。
They showed that such hierarchical RNN architectures learn more effectively from input graphs than do the traditional rule-based graph generative models while having a reasonable time complexity.
他们表明,这种层次结构的RNN体系结构比传统的基于规则的图生成模型更有效地从输入图中学习,同时具有合理的时间复杂度
To capture the temporal information of dynamic graphs, dynamic graph neural network (DGNN) [27] was proposed that used a time-aware LSTM [39] to learn node representations.
为了捕捉动态图的时间信息,[27] 提出了一种动态图神经网络(DGNN),它使用时间感知LSTM[39]来学习节点表示。
Aiming to tackle the graph sparsity problem, RMGCNN [28] applied an LSTM to the results of GCNs to progressively reconstruct a graph as illustrated in Figure 2.
为了解决图的稀疏性问题,RMGCNN[28]将LSTM应用于GCNs的结果,逐步重建图,如图2所示。
By using an LSTM, the information from different parts of the graph can diffuse across long ranges without requiring as many GCN layers.
通过使用LSTM,来自图形不同部分的信息可以在很长的范围内扩散,而不需要那么多GCN层。
Dynamic GCN [29] applied an LSTM to gather the results of GCNs from different time slices in dynamic networks to capture both the spatial and temporal graph information.
Dynamic GCN[29]应用LSTM从动态网络的不同时间片收集GCN的结果,以捕获空间和时间的图形信息。
笔者:
1.在graph-level RNNs,是把RNNs应用于整个图来进行编码
2.[26]将图RNN应用于图生成问题,他们采用了两个rnn:一个用于生成新节点,另一个用于以自回归方式为新添加的节点生成边。
3.为了捕捉动态图的时间信息,[27] 提出了一种动态图神经网络(DGNN),它使用时间感知LSTM[39]来学习节点表示。
4.为了解决图的稀疏性问题,RMGCNN[28]将LSTM应用于GCNs的结果,逐步重建图,可以减少GCN层。
5.Dynamic GCN[29]应用LSTM从动态网络的不同时间片收集GCN的结果,以捕获空间和时间的图形信息。
4.GRAPH CONVOLUTIONAL NETWORKS
Graph convolutional networks (GCNs) are inarguably the hottest topic in graph-based deep learning.
图卷积网络无疑是基于图的深度学习中最热门的研究课题。
Because most GCNs can be trained with task-specific loss via backpropagation (with a few exceptions such as the unsupervised training method in [74]),we focus on the adopted architectures.We first discuss the convolution operations, then move to the readout operations and some other improvements. We summarize the main characteristics of GCNs surveyed in this paper in Table 4.
由于大多数GCNs都可以通过反向传播进行任务特定损失的训练(除了少数例外,如[74]中的无监督训练方法),因此我们重点讨论了所采用的方法结构。我们首先讨论卷积运算,然后转到读出操作和其他一些改进。我们在表4中总结了本文调查的GCNs网络的主要特点。

笔者:
1.图卷积神经网络是当前比较热门的图研究方向
4.1Convolution Operations
Graph convolutions can be divided into two groups: spectral convolutions, which perform convolution by transforming node representations into the spectral domain using the graph Fourier transform or its extensions, and spatial convolutions, which perform convolution by considering node neighborhoods.
图卷积可以分为两类:频域卷积,它通过使用图傅里叶变换或其扩展将节点表示转换为频域来执行卷积;空域卷积通过考虑节点邻的邻接节点来执行卷积。
spectral convolutions 频域卷积(使用傅里叶变换)
spatial convolutions 空域卷积 (使用周围节点)
Note that these two groups can overlap, for example, when using a polynomial spectral kernel (please refer to Section 4.1.2 for details).
这两个方法可以重叠,例如,当使用多项式谱核时(请参阅第4.1.2节了解详细信息)。
笔者:
1.卷积方式有两种
spectral convolutions 频域卷积(使用傅里叶变换)
spatial convolutions 空域卷积(使用周围节点)
2.这两种方法可以同时使用
4.1.1Spectral Methods
Convolution is the most fundamental operation in CNNs. However, the standard convolution operation used for images or text cannot be directly applied to graphs because graphs lack a grid structure [6]. Bruna et al. [40] fifirst introduced convolution for graph data from the spectral domain using the graph Laplacian matrix L [75], which plays a similar role as the Fourier basis in signal processing [6].
卷积是CNNs中最基本的运算。然而,用于图像或文本的标准卷积运算不能直接应用于图形,因为图形缺少网格结构[6]。Bruna等人。[40]首先使用图拉普拉斯矩阵L[75]对来自谱域的图形数据引入了卷积,它在信号处理中起着类似于傅立叶基的作用[6]。
The validity of this definition is based on the convolution theorem, i.e., the Fourier transform of a convolution operation is the element-wise product of their Fourier transforms.
该定义的有效性基于卷积定理,即卷积运算的傅立叶变换是其傅立叶变换的元素积。
However, directly using Eq. (7) requires learning O(N) parameters, which may not be feasible in practice. Besides, the fifilters in the spectral domain may not be localized in the spatial domain,i.e., each node may be affected by all the other nodes rather than only the nodes in a small region.
然而,直接使用式(7)需要学习O(N)参数,这在实践中可能不可行。另外,频谱域中的滤波器可能不局限于空间域,即每个节点都可能受到所有其他节点的影响,而不仅仅是一个小区域中的节点。
To alleviate these problems,Bruna et al. [40] suggested using the following smoothing filters:
为了缓解这些问题,Bruna等人。[40]建议使用以下平滑过滤器:
![]()
However, two fundamental problems remain unsolved. First, because the full eigenvectors of the Laplacian matrix are needed during each calculation, the time complexity is at least O(N2) for each forward and backward pass, not to mention the O(N3) complexity required to calculate the eigendecomposition, meaning that this approach is not scalable to large-scale graphs. Second, because the filters depend on the eigenbasis Q of the graph, the parameters cannot be shared across multiple graphs with different sizes and structures.
然而,有两个根本问题仍未解决。首先,由于每次计算都需要拉普拉斯矩阵的全部特征向量,所以每次向前和向后的过程中,时间复杂度至少为O(N2),更不用说计算特征分解所需的O(N3)复杂度,这意味着该方法不可扩展到大规模图。第二,由于filters依赖于图的特征基Q,参数不能在不同大小和结构的多个图之间共享。
Next, we review two lines of works trying to solve these limitations and then unify them using some common frameworks.
接下来,我们回顾两种试图解决这些限制的工作,然后使用一些通用框架将它们统一起来。
笔者:
1.使用拉普拉斯矩阵会有两个问题:
(1)时间复杂度高,效率方便需要改进
(2)filters依赖图的固定结构,参数不能在不同大小、结构的图之间共享
2.下面4.1.2和4.1.3分别解决上诉两个问题
4.1.2The Effificiency Aspect 效率方面
To solve the effificiency problem, ChebNet [42] was proposed to use a polynomial fifilter as follows:
为了解决效率问题,ChebNet[42]提出使用多项式fifilter,如下所示:
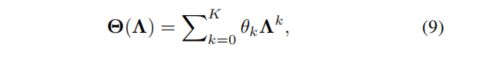
An important insight of ChebNet and its extension is that they connect the spectral graph convolution with the spatial architecture.
ChebNet及其扩展的一个重要见解是将频域卷积与空间结构联系起来。
Specifically, they show that when the spectral convolution function is polynomial or first-order, the spectral graph convolution is equivalent to a spatial convolution.
具体地说,当频卷积函数是多项式或一阶时,频域图卷积相当于空间卷积。
In addition, the convolution in Eq. (13) is highly similar to the state definition in a GNN in Eq. (1), except that the convolution definition replaces the recursive definition.
此外,式(13)中的卷积与式(1)中GNN中的状态定义高度相似,只是卷积定义代替了递归定义。
Some spectral methods have also been proposed to solve the effificiency problem. For example, instead of using the Chebyshev expansion as in Eq. (10), CayleyNet [44] adopted Cayley polynomials to defifine graph convolutions:
一些别的频域方法来解决效率问题。例如,CayleyNet[44]没有像公式(10)那样使用Chebyshev展开,而是采用Cayley多项式来定义图形卷积:
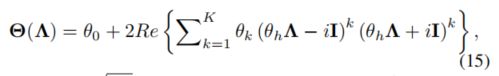
笔者:
ChebNet [42] 和CayleyNet[44]分别提出了的解决方法
ChebNet及其扩展的一个重要见解是将频域卷积与空间结构联系起来,当频卷积函数是多项式或一阶时,频域图卷积相当于空间卷积。
CayleyNet
GWNN进一步提出用图小波变换代替频滤波器中的傅里叶变换。
4.1.3The Aspect of Multiple Graphs 多种类型图方面
A parallel series of works has focuses on generalizing graph convolutions to multiple graphs of arbitrary sizes.Neural FPs [46]proposed a spatial method that also used the first-order neighbors:
一个并行系列的工作集中于将图卷积推广到任意的多个图大小。神经FPs[46]提出了一种同样使用一阶邻域的空间方法:

Because the parameters Θ can be shared across different graphs and are independent of the graph size, Neural FPs can handle multiple graphs of arbitrary sizes.
由于参数Θ可以在不同的图之间共享,并且与图的大小无关,所以神经FPs可以处理任意大小的多个图。
However, instead of considering the inflfluence of node degree by adding a normalization term, Neural FPs proposed learning different parameters Θ for nodes with different degrees. This strategy performed well for small graphs such as molecular graphs (i.e., atoms as nodes and bonds as edges), but may not be scalable to larger graphs.
然而,神经FPs没有考虑节点度的输入,而是增加归一化项,而是针对不同程度的节点提出了学习不同参数的方法。这种策略对于小图(如分子图,即原子为节点和键为边)表现良好,但可能无法扩展到较大的图。
PATCHY-SAN [47] adopted a different idea. It assigned a unique node order using a graph labeling procedure such as the Weisfeiler-Lehman kernel [78] and then arranged node neighbors in a line using this pre-defifined order.
PATCHY-SAN[47]采用了不同的想法。它使用一个图标记过程(如Weisfeiler-Lehman内核[78])指定一个唯一的节点顺序,然后使用这个预先定义的顺序将节点邻居排成一行。
PATCHY-SAN can learn from multiple graphs like normal CNNs learn from multiple images。
PATCHY-SAN可以从多个图中学习,就像普通CNNs从多个图像中学习一样
The drawbacks are that the convolution depends heavily on the graph labeling procedure which is a preprocessing step that is not learned.
缺点是卷积很大程度上依赖于图标记过程,这是一个没有学习的预处理步骤。
LGCN [48] further proposed to simplify the sorting process by using a lexicographical order (i.e., sorting neighbors based on their hidden representation in the fifinal layer HL)
LGCN[48]进一步提出通过使用字典序(即,基于其在第五层HL中的隐藏表示对邻域进行排序)来简化排序过程。
DCNN [50] adopted another approach by replacing the eigenbasis of the graph convolution with a diffusion-basis, i.e., the neighborhoods of nodes were determined by the diffusion transition probability between nodes. Specififically, the convolution was defifined as follows:
DCNN[50]采用另一种方法,用扩散基代替图卷积的特征基,即节点的邻域由节点间的扩散转移概率决定。具体而言,卷积定义如下:

笔者:
1.FPs[46]、PATCHY-SAN [47] 、LGCN[48]、DCNN[50]陆续提出方法解决图结构问题
4.1.4 Frameworks
Based on the above two lines of works, MPNNs [52] were proposed as a unifified framework for the graph convolution operation in the spatial domain using message-passing functions:
基于以上两个方面的工作,MPNNs[52]被提出作为空域中使用消息传递函数进行图形卷积运算的统一框架:
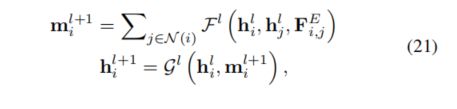
Conceptually, MPNNs are a framework in which each node sends messages based on its states and updates its states based on messages received from the immediate neighbors.
从概念上讲,MPNNs是一个框架,其中每个节点根据其状态发送消息,并根据从相邻节点接收到的消息更新其状态。
The authors showed that a specifific variant of MPNNs could achieve state-of-the-art performance in predicting molecular properties.
作者认为,MPNNs的一个特定变体可以在预测分子性质方面达到最新的性能。
Concurrently, GraphSAGE [53] took a similar idea as Eq. (21) using multiple aggregating functions as follows:

In summary, the convolution operations have evolved from the pectral domain to the spatial domain and from multistep neighbors to the immediate neighbors. Currently, gathering information from the immediate neighbors (as in Eq. (14)) and following the framework of Eqs. (21)(22)(27) are the most common choices for graph convolution operations.
综上所述,卷积运算已经从频域发展到空域,从多步邻域到直接邻域。目前,从近邻收集信息(如等式(14))并遵循Eqs(21)(22)(27)的框架,是图卷积运算最常见的选择。
笔者:
1.MPNNs[52]被提出作为空间域中使用消息传递函数进行图形卷积运算的统一框架
2.卷积运算已经多方面发展了
4.2Readout Operations 读出操作
Using graph convolution operations, useful node features can be learned to solve many node-focused tasks.However, to tackle graph-focused tasks, node information needs to be aggregated to form a graph-level representation.
利用图卷积运算,可以学习有用的节点特征来解决多个节点集中的问题任务。但是为了解决以图为中心的任务,需要聚合节点信息,形成图形级表示。
In the literature, such procedures are usually called the readout operations
在文献中,这种程序通常被称为读出操作
Order invariance. 节点的顺序不变性,即节点的顺序不会影响最后的结果
we only can find a function that is orderinvariant but not vice versa in a polynomial time, i.e., even two structurally different graphs may have the same representation.
在多项式时间内,我们只能找到一个序不变的函数,反之亦然,即即使两个结构不同的图也可能有相同的表示。
笔者:
1.
4.2.1Statistics 计算/统计
The most basic order-invariant operations involve simple statistics such as summation, averaging or max-pooling [46], [50], i.e.,
最基本的阶不变运算涉及简单的统计信息,例如求和、平均或最大池[46]、[50],即。,

Kearnes et al. [55] suggested considering the distribution of node representations by using fuzzy histograms [81].
卡恩斯等人。[55]建议使用模糊直方图来考虑节点表示的分布[81]。
Another commonly used approach for aggregating node representation is to add a fully connected (FC) layer as the fifinal layer [40], i.e.,
聚集节点表示的另一种常用方法是添加一个完全连接(FC)层作为第五层[40],即。,
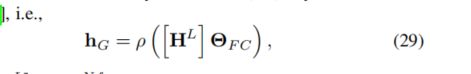
this ability comes at the cost of being unable to guarantee order invariance.
这种能力的代价是无法保证顺序不变。
笔者:
1.基础运算:求和、求平均、池化
2.卡恩斯用模糊直方图统计
3.使用全连接神经网络,缺点是无法保证节点顺序的不变性
4.2.2Hierarchical Clustering 层次聚类
Rather than a dichotomy between node and graph level structures, graphs are known to exhibit rich hierarchical structures [82], which can be explored by hierarchical clustering methods as shown in Figure 4. For example, a density-based agglomerative clustering [83] was used in Bruna et al. [40] and multi-resolution spectral clustering [84]was used in Henaff et al.
[41]. ChebNet [42] and MoNet [54] adopted another greedy hierarchical clustering algorithm, Graclus [85], to merge two nodes at a time, along with a fast pooling method to rearrange the nodes into a balanced binary tree. ECC [63] adopted another hierarchical clustering method by performing eigendecomposition [86].
图不是节点级结构和图级结构之间的二分法,而是已知的具有丰富层次结构的图[82],可以通过图4所示的层次聚类方法对其进行研究。例如,Bruna等人使用了基于密度的凝聚聚类[83]。[40]和多分辨率光谱聚类[84]被用于Henaff等人。
[41]。ChebNet[42]和MoNet[54]采用了另一种贪婪的层次聚类算法Graclus[85],一次合并两个节点,同时使用快速池方法将节点重新排列成平衡的二叉树。ECC[63]通过执行特征分解,采用了另一种层次聚类方法[86]。
However,these hierarchical clustering methods are all independent of the graph convolutions (i.e., they can be performed as a preprocessing step and are not trained in an end-to-end fashion).
这些层次聚类方法都独立于图的卷积(也就是说,它们可以作为一个预处理步骤来执行,并且不以端到端的方式进行训练)。
To solve that problem, DiffPool [56] proposed a differentiable hierarchical clustering algorithm jointly trained with the graph convolutions.
为了解决这个问题,DiffPool[56]提出了一种结合图卷积训练的可微层次聚类算法。
笔者:
不懂
4.2.3Imposing Orders and Others 执行命令和其他
As mentioned in Section 4.1.3, PATCHY-SAN [47] and SortPooling [49] took the idea of imposing a node order and then resorted to standard 1-D pooling as in CNNs.
如第4.1.3节所述,PATCHY-SAN[47]和SortPooling[49]采用了强制节点顺序的思想,然后像CNNs一样求助于标准的一维池。
笔者:
不懂
4.2.4Summary
In short, statistics such as averaging or summation are the most simple readout operations, while hierarchical clustering algorithms jointly trained with graph convolutions are more advanced but are also more sophisticated. Other methods such as adding a pseudo node or imposing a node order have also been investigated.
简言之,诸如平均或求和之类的统计量是最简单的读出操作,而与图卷积联合训练的层次聚类算法更先进,但也更复杂。其他方法,如添加一个伪节点或施加一个节点顺序也被研究过。
笔者:
readout方法有很多
4.3Improvements and Discussions
Many techniques have been introduced to further improve GCNs.Note that some of these methods are general and could be applied to other deep learning models on graphs as well.
为了进一步改进GCNs在未来将引入很多技术.注意这些方法具有通用性,也可应用于其它图形深度学习模型。
笔者:
GCNs引用了别的网络的许多技术,也可以把应用于图网络的方法应用到别的神经网络模型
4.3.1Attention Mechanism attention机制
In the aforementioned GCNs, the node neighborhoods are aggregated with equal or pre-defined weights.However, the influences of neighbors can vary greatly; thus, they should be learned during training rather than being predetermined.
在上述的GCNs中,节点邻域用相等或预定义的方式聚合重量。但是邻接节点的影响会有很大的差异,因此,应该在训练中学习,而不是预先确定。
HAN [59] proposed a two-level attention mechanism, i.e., anode-level and a semantic-level attention mechanism, for heterogeneous graphs.
韩[59]提出了一种两级注意机制,即节点级和语义级的注意机制,用于异构图。
笔者:Attention机制
4.3.2Residual and Jumping Connections 残差链接和跳跃连接
They showed experimentally that adding such residual connections could allow the depth of the network to increase, which is similar to the results of ResNet.
他们通过实验证明,添加这种剩余连接可以使网络的深度增加,这与ResNet的结果相似。
Column network (CLN) [60] adopted a similar idea by using the following residual connections with learnable weights:
列网络(CLN)[60]采用了类似的思想,使用了以下具有可学习权重的残差连接:

Jumping knowledge networks (JK-Nets) [62] proposed another architecture to connect the last layer of the network with all the lower hidden layers, i.e., by “jumping” all the representations to the final output, as illustrated in Figure 6.
跳跃知识网络(JK Nets)[62]提出了另一种架构,将网络的最后一层与所有较低的隐藏层连接起来,即通过将所有表示“跳跃”到最终输出,如图6所示。
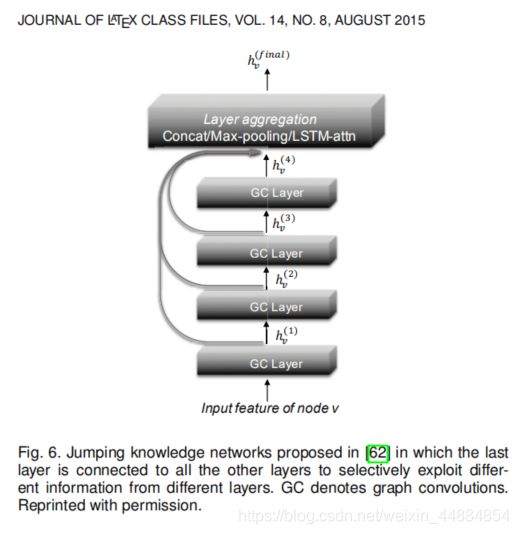
笔者:
1.残差连接和跳跃连接可以把前面得到的数据直接传到后面,可以使很深的网络仍保留之前的一些信息
4.3.3Edge Features 边缘特征
The aforementioned GCNs mostly focus on utilizing node features and graph structures. In this subsection, we brieflfly discuss how to use another important source of information: the edge features.
上述的GCNs主要集中在利用节点特征和图结构上。在本小节中,我们将简要讨论如何使用另一个重要的信息源:边缘特征。
DCNN [50] proposed another method to convert each edge into a node connected to the head and tail node of that edge.
DCNN[50]提出了另一种方法,将每条边转换成一个连接到该边的头和尾节点的节点。
In other words, nodes in the line graph are directed edges in the original graph, and two nodes in the line graph are connected if information can flow through their corresponding edges in the original graph. Then, LGCN adopted two GCNs: one on the original graph and one on the line graph.
换句话说,线图中的节点是原始图中的有向边,如果信息可以通过原始图中相应的边,则线图中的两个节点是连通的。然后,LGCN采用了两个GCNs:一个在原始图上,一个在线图上。
Kearnes et al. [55] proposed an architecture using a “weave module”. Specifically, they learned representations for both nodes and edges and exchanged information between them in each weave module using four different functions: node-to-node (NN), node to-edge (NE), edge-to-edge (EE) and edge-to-node (EN):
卡恩斯等人。[55]提出了一种使用“编织模块”的体系结构。具体来说,他们学习了节点和边的表示,并使用四种不同的函数在每个编织模块中交换它们之间的信息:节点到节点(NN)、节点到边(NE)、边到边(EE)和边到节点(EN):

笔者:
1.边特征好像是图网络中没有注意到的点
2.为取得边特征,可以把边当作点来构建图模型,具体操作见论文
4.3.4Sampling Methods 采样方法
One critical bottleneck when training GCNs for large-scale graphs is effificiency.
在训练大规模图的GCNs时,一个关键的瓶颈是效率。
To deal with this problem, two types of sampling methods have been proposed: neighborhood samplings and layer-wise samplings, as illustrated in Figure 7.
为了解决这个问题,提出了两种类型的抽样方法:邻域抽样和分层抽样,如图7所示。
In neighborhood samplings, the sampling is performed for each node during the calculations.
在邻域采样中,在计算期间对每个节点执行采样。
GraphSAGE [53] uniformly sampled a fixed number of neighbors for each node during training
GraphSAGE[53]在训练过程中为每个节点均匀地采样了固定数量的邻居
PinSage [66] proposed sampling neighbors using random walks on graphs along with several implementation improvements including coordination between the CPU and GPU, a map-preduce inference pipeline, and so on.
PinSage[66]提出了在图上使用随机游动的抽样邻域,以及一些实现改进,包括CPU和GPU之间的协调、映射生成推理管道等。
StochasticGCN [67] further proposed reducing the sampling variances by using the historical activations of the last batches as a control variate, allowing for arbitrarily small sample sizes with a theoretical guarantee.
随机抽样[67]进一步提出通过使用最后一批的历史激活作为控制变量来减少抽样方差,允许在理论上保证任意小的样本量。
Instead of sampling neighbors of nodes, FastGCN [68] adopted a different strategy: it sampled nodes in each convolutional layer (i.e., a layer-wise sampling) by interpreting the nodes as i.i.d. samples and the graph convolutions as integral transforms under probability measures.
FastGCN[68]采用了一种不同的策略,即在每个卷积层(即分层抽样)中采样节点,将节点解释为i.i.d.样本,将图卷积解释为概率测度下的积分变换。
FastGCN also showed that sampling nodes via their normalized degrees could reduce variances and lead to better performance
FastGCN 还表明,通过归一化度采样节点可以减少方差,提高性能
笔者:
1.两种类型的抽样方法:邻域抽样和分层抽样
2.GraphSAGE[53]在训练过程中为每个节点均匀地采样了固定数量的邻居
3.PinSage[66]提出了在图上使用随机游动的抽样邻域
4.FastGCN[68]在每个卷积层(即分层抽样)中采样节点,将节点解释为i.i.d.样本,将图卷积解释为概率测度下的积分变换。
4.3.5Inductive Setting 感知设计
Another important aspect of GCNs is that whether they can be applied to an inductive setting, i.e., training on a set of nodes or graphs and testing on another unseen set of nodes or graphs
GCNs的另一个重要方面是它们是否可以应用于归纳环境,即在一组节点或图上进行训练,并在另一组没有见过的节点或图上进行测试
In principle,this goal is achieved by learning a mapping function on the given features that are not dependent on the graph basis and can be transferred across nodes or graphs.
原则上,这一目标是通过学习给定特征的映射函数来实现的,这些特征不依赖于图的基础,并且可以在节点或图之间传递。
However, the existing inductive GCNs are suitable only for graphs with explicit features.How to conduct inductive learnings for graphs without explicit features, usually called the out-of-sample problem [92], remains largely open in the literature.
然而,现有的归纳GCNs只适用于显式的图特色。怎么做进行归纳对于没有明确特征的图的学习,通常被称为样本外问题[92],在文献中仍然很大程度上是开放的(还有很大的提升空间)。
笔者:
1.GCNs的一个重要方面是他们是否有很好的泛化能力。
2.现有的GCNs只能归纳有明显特征的图,然而对于一些没用明确特征的图,在研究领域基本还是一片空白
4.3.6 Theoretical Analysis 理论分析
三类:node-focused tasks, graph-focused tasks, and general analysis
-
node-focused tasks
For node-focused tasks, Li et al. [70] fifirst analyzed the performance of GCNs by using a special form of Laplacian smoothing, which makes the features of nodes in the same cluster similar. The original Laplacian smoothing operation is formulated as follows:
对于节点集中的任务,Li等人。[70]第五章利用拉普拉斯平滑的特殊形式分析了GCNs的性能,使同一簇中节点的特征相似。原始拉普拉斯平滑操作的公式如下:

-
gragp-focused tasks
They showed that GCNs are conceptually a generalization of the WL kernel because both methods iteratively aggregate information from node neighbors.
他们表明,gcn在概念上是WL核的推广,因为这两种方法都迭代地聚集来自节点邻居的信息。 -
general analysis
Scarselli et al. [93] showed that the Vapnik-Chervonenkis dimension (VC-dim) of GCNs with different activation functions has the same scale as the existing RNNs.
Scarselli等人。[93]表明,不同激活函数的GCNs的Vapnik-Chervonenkis维数(VC-dim)与现有RNN具有相同的尺度。
笔者:
不懂
5 GRAPH AUTOENCODERS 图自动编码器
The autoencoder (AE) and its variations have been widely applied in unsupervised learning tasks [95] and are suitable for learning node representations for graphs.
自动编码器(AE)及其变体已广泛应用于无监督学习任务[95],适合于学习图的节点表示。
The implicit assumption is that graphs have an inherent, potentially nonlinear low-rank structure.
潜在的假设它具有固有的,潜在的非线性低阶结构
笔者:
1.自动编码器(AE)及其变体已广泛应用于无监督学习任务
2.使用此网络的隐性条件是Graph具有固有的、潜在的非线性低阶结构
5.1 Autoencoders
The basic idea is that, by regarding the adjacency matrix or its variations as the raw features of nodes, AEs can be leveraged as a dimensionality reduction technique to learn low dimensional node representations
其基本思想是通过将邻接矩阵或其变化作为节点的原始特征,利用AEs作为一种降维技术来学习低维节点表示
5.2 Variational Autoencoders 变分自动编码器
Different from the aforementioned autoencoders, variational autoencoders (VAEs) are another type of deep learning method that combines dimensionality reduction with generative models.
与上述的自编码不同,变分自编码(VAEs)是将降维与生成模型相结合的另一种深度学习方法。
5.3 Improvements and Discussions 改进和讨论
Several improvements have also been proposed for GAEs.
对GAEs也提出了一些改进
5.3.1 Adversarial Training 对抗训练
Specifically, the encoder of GAEs was used as the generator while the discriminator aimed to distinguish whether a latent representation came from the generator or from a prior distribution.
具体地说,GAEs的编码器被用作生成器,而鉴别器的目的是区分潜在表示是来自生成器还是来自先验分布
Concurrently, NetRA [105] also proposed using a generative adversarial network (GAN) [115] to enhance the generalization ability of graph autoencoders.
同时,NetRA[105]还提出了使用生成对抗网络(generative atterial network,GAN)[115]来增强图形自动编码器的泛化能力。
笔者:
1.NetRA[105]使用了GAN来增强图形自编码器的泛化能力
5.3.2 Inductive Learning 归纳学习
Similar to GCNs, GAEs can be applied to the inductive learning setting if node attributes are incorporated in the encoder.
与GCNs类似,如果在编码器中加入节点属性,GAEs可以应用于归纳学习设置。
5.3.3 Similarity Measures 相似性度量
More research is needed to understand the underlying differences between these metrics.
需要更多的研究来了解这些度量标准之间的潜在差异。
6 GRAPH REINFORCEMENT LEARNING 图强化学习

One aspect of deep learning not yet discussed is reinforcement learning (RL), which has been shown to be effective in AI tasks such as playing games.
深度学习的一个尚未讨论的方面是强化学习(RL),它已经被证明在诸如玩游戏这样的人工智能任务中是有效的
GCPN [116] utilized RL to generate goal-directed molecular graphs while considering non-differential objectives and constraints.
GCPN[116]利用RL生成目标定向分子图,同时考虑非微分目标和约束
By treating agent actions as link predictions, using domain-specifific as well as adversarial rewards, and using GCNs to learn the node representations, GCPN can be trained in an end-to-end manner using a policy gradient.
通过将代理行为视为链路预测,使用领域指定和对抗性奖励,并使用GCNs学习节点表示,可以使用策略梯度对GCPN进行端到端的训练。
A concurrent work, MolGAN [117], adopted a similar idea of using RL for generating molecular graphs. However, rather than generating the graph through a sequence of actions, MolGAN proposed directly generating the full graph; this approach worked particularly well for small molecules.
MolGAN[117]的一项并行工作采用了类似的想法,即使用RL来生成分子图。然而,MolGAN建议直接生成完整的图形,而不是通过一系列的动作生成图形;这种方法对小分子特别有效。
GTPN [118] adopted RL to predict chemical reaction products.
GTPN[118]采用RL预测化学反应产物。
GAM [119] applied RL to graph classification by using random walks.
GAM[119]使用随机步将RL应用于图的分类。
DeepPath [120] and MINERVA [121] both adopted RL for knowledge graph (KG) reasoning.
deepath[120]和MINERVA[121]都采用RL进行知识图(KG)推理。
7 GRAPH ADVERSARIAL METHODS 图对抗方法
Adversarial methods such as GANs [115] and adversarial attacks have drawn increasing attention in the machine learning community in recent years.
近年来,GANs[115]和对抗攻击等对抗性攻击方法在机器学习中越来越受到重视。
7.1 Adversarial Training 对抗性训练
The basic idea behind a GAN is to build two linked models: a discriminator and a generator. The goal of the generator is to “fool” the discriminator by generating fake data, while the discriminator aims to distinguish whether a sample comes from real data or is generated by the generator.
GAN背后的基本思想是建立两个相互联系的模型:鉴别器和发生器。生成器的目标是通过生成假数据来“愚弄”鉴别器,而鉴别器的目标是区分样本是来自真实数据还是由生成器生成的。
Adversarial training has been shown to be effective in generative models and enhancing the generalization ability of discriminative models.
对抗训练在生成模型和提高判别模型的泛化能力方面是有效的。
Similar to ARGA [104], ANE used a GAN as an additional regularization term to existing network embedding methods such as DeepWalk [131] by imposing a prior distribution as the real data and regarding the embedding vectors as generated samples.
与ARGA[104]类似,ANE将GAN作为现有网络嵌入方法(如DeepWalk[131])的附加正则化项,将先验分布作为真实数据,并将嵌入向量视为生成的样本。
笔者:
1.GAN就像老师和学生,学生要写出好的作业给老师看,老师进行打分,等到学生分数很高的时候,学生就可以出师了
7.2 Adversarial Attacks 对抗性攻击
Adversarial attacks are another class of adversarial methods intended to deliberately “fool” the targeted methods by adding small perturbations to data.
对抗性攻击是另一类对抗性方法,旨在通过向数据中添加小扰动来故意“愚弄”目标方法。
Nettack [128] first proposed attacking node classifification models such as GCNs by modifying graph structures and node attributes.
Nettack[128]首先通过修改图结构和节点属性,提出了攻击节点分类模型,如GCNs
Simply speaking, the optimization aims to fifind the best legitimate changes in graph structures and node attributes to cause v0 to be misclassifified.
简单地说,优化的目的是找出图结构和节点属性的最佳合法变化,从而导致v0被错误分类。
The aforementioned two attacks are targeted, i.e., they are intended to cause misclassifification of some targeted node v0. Zugner and Gunnemann [130] were the fifirst to study non-targeted attacks, which were intended to reduce the overall model performance. They treated the graph structure as hyper-parameters to be optimized and adopted meta-gradients in the optimization process, along with several techniques to approximate the meta-gradients.
上述两种攻击都是有针对性的,也就是说,它们旨在导致某些目标节点v0的错误分类。Zugner和Gunnemann[130]是第一个研究非目标攻击的人,这些攻击旨在降低模型的整体性能。他们将图结构视为需要优化的超参数,在优化过程中采用了元梯度,并采用了几种近似元梯度的技术。
笔者:
1.Adversarial Attacks 是对元数据进行数据扰动进行‘攻击’
8 DISCUSSIONS AND CONCLUSION 讨论和结论
Thus far, we have reviewed the different graph-based deep learning architectures as well as their similarities and differences. Next, we brieflfly discuss their applications, implementations, and future directions before summarizing this paper.
到目前为止,我们已经回顾了不同的基于图的深度学习架构,以及它们的异同。接下来,在总结本文之前,我们将简要讨论它们的应用、实现和未来的方向。
8.1 Applications 应用
In addition to standard graph inference tasks such as node or graph classifification10, graph-based deep learning methods have also been applied to a wide range of disciplines, including modeling social inflfluence [133], recommendation [28], [66], [99], [134], chemistry and biology [46], [52], [55], [116], [117], physics [135], [136], disease and drug prediction [137]–[139], gene expression [140], natural language processing (NLP) [141], [142], computer vision [143]–[147], traffific forecasting [148], [149], program induction [150], solving graph-based NP problems [151], [152], and multi-agent AI systems [153]–[155].
除了标准的图形推理任务(如节点或图形分类10),基于图形的深度学习方法也被应用于广泛的学科领域,包括建模社会影响[133]、建议[28]、[66]、[99]、[134]、化学和生物学[46]、[52]、[55]、[116]、[117]、物理[135]、[136]、疾病和药物预测[137]–[139],基因表达[140],自然语言处理(NLP)[141],[142],计算机视觉[143]–[147],交通预测[148],[149],程序归纳[150],解决基于图形的NP问题[151],[152],以及多智能体人工智能系统[153]–[155]。
First,it is important to incorporate domain knowledge into the model when constructing a graph or choosing architectures
首先,在构造图或选择体系结构时,将领域知识纳入模型是很重要的
Second, a graph-based model can usually be built on top of other architectures rather than as a stand-alone model.
其次,基于图的模型通常可以建立在其他体系结构之上,而不是作为一个独立的模型。
笔者:
1.图神经网络现在应用于多个方面
2.在选择图神经网络时,最好将相关领域的知识纳入模型。比如化学:原子间的键是有限制的、有些化合物不能共存,选择模型时需要将它们这些限制因素考虑进去
8.2 Implementations 实施
Recently, several open libraries have been made available for developing deep learning models on graphs
最近,有几个开放的库被用来开发图的深度学习模型
笔者:文章末尾给出了深度学习模型,具体见论文
8.3 Future Directions
-
New models for unstudied graph structures 非研究图的新模型
Due to the extremely diverse structures of graph data, the existing methods are not suitable for all of them.所以需要一个新的模型来解决问题 -
Compositionality of existing models. 现有模型的组成
-
Dynamic graphs 动态图
Some preliminary works have obtained encouraging results by using Graph RNNs
利用图RNNs进行了一些初步工作,取得了令人鼓舞的结果 -
Interpretability and robustness 可解释性和鲁棒性
Some pioneering works regarding interpretability and robustness can be found in [161] and [162], [163], respectively.
在解释性和鲁棒性方面的一些开创性著作分别见于[161]和[162]、[163]。
笔者:
未来图网络在很多地方还是有很大的发展:
1.现在不存在的模型:可以开发一种新型的图网络结构来解决一些问题,超图(Hypergraphs)
2.将现有的模型结合:如残差网络、GAN、Attention机制等等,都可以和图相结合
3.动态图:向原有的图进行删除/增加 边/节点,会使网络结构发生变化
4.可解释性和鲁棒性:图的可解释性比传统神经网络的‘黑盒’更难,因为图具有更加复杂的结构
8.4 Summary
The above survey shows that deep learning on graphs is a promising and fast-developing research fifield that both offers exciting opportunities and presents many challenges. Studying deep learning on graphs constitutes a critical building block in modeling relational data, and it is an important step towards a future with better machine learning and artifificial intelligence techniques.
以上调查表明,图的深度学习是一个很有前途、发展迅速的研究领域,既提供了令人兴奋的机会,也带来了许多挑战。研究图的深度学习是关系数据建模的一个重要组成部分,它是朝着更好的机器学习和人工智能技术的未来迈出的重要一步。