神经网络基础知识及模型优化(一)
神经网络基础知识及模型优化(一)
- 前言
- 一、神经网络参数更新及其方法
-
- 1.参数更新
- 2.SGD
- 3.Momentum
- 4. AdaGrad
- 5.Adam
- 6.该使用哪种参数更新方法
- 二、权重的初始化
-
- 1.可以将权重初始值设置为0吗
- 2.隐藏层的激活值的分布
- 3.ReLU函数的权重初始化
- 三、Batch Normalization
-
- 1.Batch Normalization的算法
- 2.Batch Normalization的评估
- 3.Batch Norm奏效的原因
- 参考文献
- 总结
前言
最近看了西瓜书、深度学习入门:基于Python的理论与实现、吴恩达老师的深度学习笔记等等,由于可能看的东西太多,有些东西看了就忘,因此决定以此方式进行一个记录。这里不会去详细阐述神经网络的结构之类的,而是把一些比较有用的,用于加深理解的,或者以后优化模型可能会用到的知识点进行简单的整理。
一、神经网络参数更新及其方法
1.参数更新
神经网络的学习是为了找到使损失函数的值尽可能小的参数,而寻找最优参数问题的方法很多,接下来将逐步
介绍SGD、Momentum、AdaGrad、Adam。
2.SGD
SGD,即随机梯度下降算法,其更新参数的公式如下。其中,w为权重参数,n为学习率。
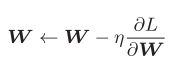
这里,我们不详细介绍SGD,仅对其缺点进行阐述。SGD虽然简单易实现,但是他对于非均向的函数,其参数的搜索更新就会变得非常低效,而其根本原因在于参数的更新并没有指向最小值的方向。
假设存在函数
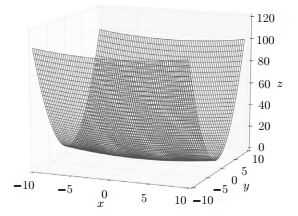
f ( x , y ) = 1 20 x 2 + y 2 f(x,y)= \frac{1}{20}x^2+y^2 f(x,y)=201x2+y2
该函数图像如下所示:
我们可以直观的感受到,该函数通过改变x轴变化的影响远远小于改变y轴变化的影响。即该函数在y轴上的梯度大,在x轴上的梯度小。并且通过观察该函数梯度的指向,可以直观地看到许多点的梯度并没有指向使该函数值最小的点(0,0)。具体梯度图如下图:
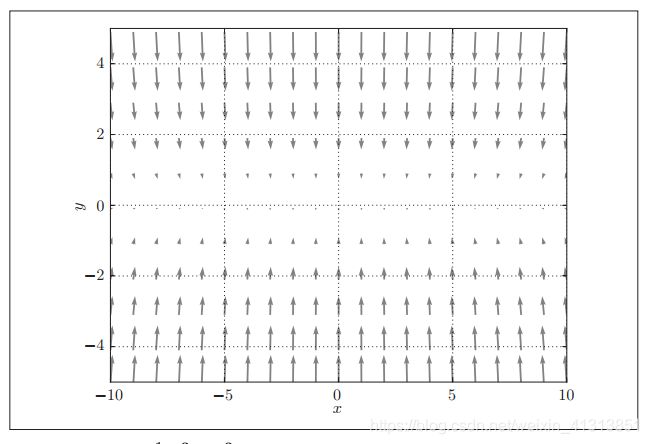
因此,在这种情况下,使用SGD方式更新参数的过程会变得比较“曲折”,需要走许多弯路才能最终找到最优的参数,整个参数的迭代更新如下图所示。
可以明显看到,整个参数的更新呈之字型,这显然不是好的参数迭代更新的方法接下来会介绍另外几种参数更新的方法,能够一定程度上解决这一问题。
3.Momentum
Momentum是“动量”的意思,该算法的运行速度几乎总是快于标准的梯度下降算法。而该方法来进最优化参数也跟物理上的动量有一定类似。用数学式子表示Momentum方法如下式。
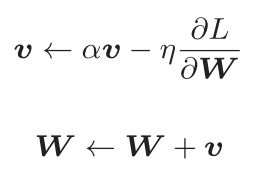
这里出现了一个新的变量v,对应于物理上的速度。其表示了物体在梯度方向的受力,而在这个力的作用上,物体速度的增加变化。如下图所示,Momentum方法感觉就像是一个小球在地面上滚动。

式子中,α一般设定为0.9,该参数承担使物体逐渐减速的任务,对应于物理中的摩擦力或空气阻力。
仍用函数 f ( x , y ) = 1 20 x 2 + y 2 f(x,y)= \frac{1}{20}x^2+y^2 f(x,y)=201x2+y2 作为例子,该方法与SGD相比,其参数更新中”之“字形减轻了很多。因为虽然在 x x x轴上受力很小,但一直保持同一个方向,所以朝同一个方向有一定的加速。同样的,尽管在 y y y轴上受力较大,但是由于受到的力方向相反,会相互的低效,所以 y y y轴上的速度不稳定,能够更快地朝着 x x x轴方向靠近,减轻“之”字形。具体参数最优化更新路径如下图。
4. AdaGrad
在学习率η的设置技巧中,有一种叫做学习率衰减的方法,即随着学习的进行,使学习率逐渐减小。即先设置较大的学习率,然后逐渐减少。AdaGrad方法会为参数每个元素适当的调整学习率,其参数更新公式如下所示。
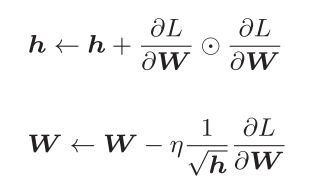
其中,出现了一新的变量 h h h,它用于保存以往所有的梯度值的平方和。而在更新参数的时候,通过乘以 1 h \frac{1}{\sqrt{h}} h1来调整学习率,它可以根据每个元素来进行学习率衰减,使得变动大的参数的学习率逐渐减小。因此随着学习的深入,更新的幅度就会逐渐减小。
然而,AdaGrad方法存在一个问题是,如果无止境的学习,更新量就会变成0,即完全不再更新。为了解决这个问题,可以使用RMSProp方法,RMSProp方法和AdaGrad方法唯一的区别是,其在计算 h h h时并不是将所有梯度一视同仁的相加,而是逐渐遗忘过去的梯度,将新的梯度信息赋予更高的权重,更好的体现出来。从专业的角度上讲,称为“指数移动平均”,即呈指数函数式的减小过去的梯度尺度。
同时,在使用AdaGrad方法时候,为了防止更新量变为0的情况,可以在 1 h \frac{1}{\sqrt{h}} h1的基础上加上一个微小值。最终AdaGrad方法进行函数 f ( x , y ) = 1 20 x 2 + y 2 f(x,y)= \frac{1}{20}x^2+y^2 f(x,y)=201x2+y2的参数最优化搜索路径图如下图所示。
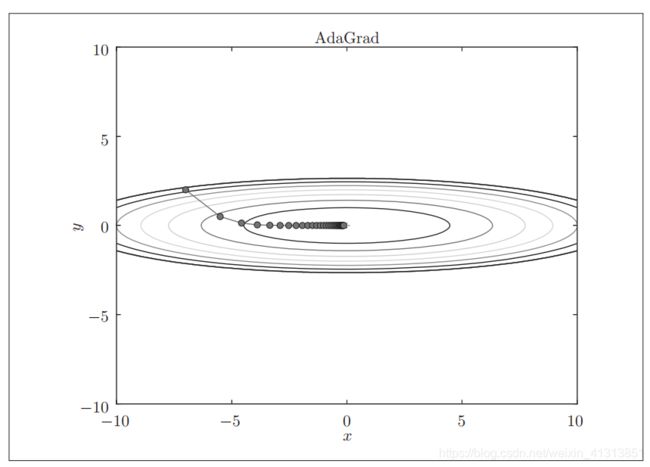
如图可以看到,由于 y y y轴上梯度较大,因此刚开始变动很大,也正因为其刚开始变动较大,之后会按比例减少其更新的步伐,因此在 y y y轴上的更新程度被大大减弱,“之”字形明显衰减。
5.Adam
Momentum方法参照小球在碗中移动的物理规则进行移动,AdaGrad为参数的每个元素适当的调整更新步伐,而Adam则将两个方法融合在了一起。
直观的,可以将Adam方法想象成一个小球在碗中滚动,但由于结合了AdaGrad方法使得学习的更新程度被适当的调整了,因此Adam小球的左右摇晃程度有所减轻。Adam方法的参数最优化更新路径图如下图所示。
6.该使用哪种参数更新方法
很遗憾,并不存在能解决所有问题的良好方法,四个方法各有各的特点。其中最经典的肯定属SGD。但是,目前人们越来越趋向于使用Adam方法。
二、权重的初始化
1.可以将权重初始值设置为0吗
先上结论,不可以!因为如果某一层的权重全部为0,那么下一层的神经网络会全部传递同样的值,这意味着反向传播的时候权重会进行完全相同的更新,因此神经网络的权重被更新为相同的值,使得其权重失去了意义。
2.隐藏层的激活值的分布
接下来,我们将观察权重初始值是如何影响隐藏层输出的分布。接下来通过一个实验,向一个5层的神经网络随即生成输入数据并观察输出数据的分布。假设每层都有100个神经元,然后随机生成满足高斯分布的1000个数据作为输入数据,激活函数选择sigmoid函数,而权重的尺度选择为标准差为1的高斯分布,接下来观察神经网络各层的激活值数据,如下图。

可以看到,各层的激活值都偏向0和1,而由于选用的激活函数是sigmoid函数,随着输出不断靠近0或1,其导数值逐渐接近0,因此会造成梯度消失的情况。而随着训练层次的加深,梯度消失的情况会变得更加严重。
接下来将权重的尺度改为标准差为0.01的高斯分布并观察神经网络各层的激活值数据,如下图。
可以明显地看到,这一次激活值的数据集中在0.5附近,不再像上一个例子一样偏向0和1,因此不再会发生梯度消失的问题。但是这一次激活值的分布有所偏向,即太多的神经元输出了类似的值,那它们就没有什么存在的意义了,因为如果100个神经元几乎都输出了相同的值,那么跟1个神经元所表达的事情基本相同。因此,如果存在这激活值分布有所偏向的情况会出现“表现力受限”的问题。即,激活值的分布需要有适当的广度,这样才能进行高效的学习。
接下来,我们使用了Xavier在论文中提出的一种新的方法设置权重初始值。论文中,为了使各层激活值具有相同的广度,推导除了合适的权重尺度,即如果前一层的节点数为 n n n,则初始值使用标准差为 1 n \frac{1}{\sqrt{n}} n1的分布。
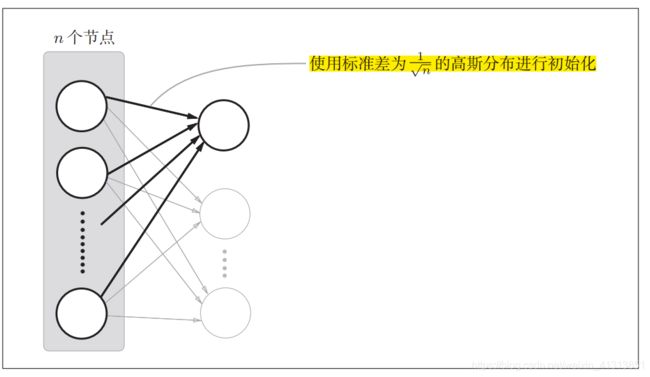
使用Xavier初始值后,如果钱一层的节点数越多,那么要设定为目标结点的初始值的权重尺度就越小。最终,使用Xavier方法进行参数初始化后,激活值的分布如下图所示。可以明显看到,相比之前更有广度的分布,因此sigmoid函数的表现力不受限制,能进行更加高效的学习。
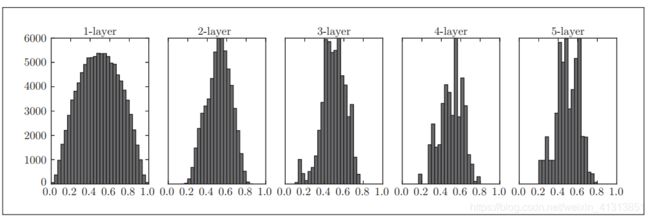
实际上,我们可以看到,在神经网络的后几层激活函数的分布稍显“不均匀”,实际上如果用 t a n h tanh tanh函数代替sigmoid函数这个稍微歪斜的函数就能得到改善,因为sigmoid函数是关于(0,0.5)对称的S型曲线,而tanh函数是关于原点(0,0)对称的S型曲线,而众所周知,用作激活函数的函数最好具有关于原点对称的性质。
3.ReLU函数的权重初始化
当激活函数选择ReLU函数的时候,我们一般采用其专门的权重初始化方式,即当前一层的节点数为 n n n时,初始值使用标准差为 2 n \sqrt{\frac{2}{n}} n2的高斯分布,从直观意义上我们可以理解为,由于ReLU函数的负值区间为0,为了使其更有广度,因此需要使用两倍的系数。
接下来我们通过实验对比了,当激活函数使用ReLU函数时,分别通过标准差为0.01的高斯分布、初始值为Xavier方式生成以及初始值采用ReLU专门的权重初始化方法生成时激活值的分布情况对比,具体如下图所示。

通过图中的对比我们可以看出,以标准差为0.01的高斯分布生成的参数,其各层的激活值非常小,并且极大部分均为0,会出现梯度消失的情况,同样使学习难以有效进行。而采用Xavier方式进行初始化时,前几层的激活函数效果尚可,但随着层次的加深,激活值的偏向变大,逐渐出现梯度消失的问题,广度不足。而采用ReLU专门的生成方式即使层次加深,也能维持较好的广度。
综上所述,当激活函数使用ReLU函数时,采用ReLU函数专门的权重初始化方式。当激活函数为sigmoid或tanh等S型曲线函数时,初始值使用Xavier方式。
三、Batch Normalization
1.Batch Normalization的算法
Batch Normalization算法是基于想要“强制性”的调整激活值的分布这一想法而产生的。其具有以下优点:
(1)可以是学习更加快速的进行。
(2)降低对初始值的依赖。
(3)抑制过拟合。
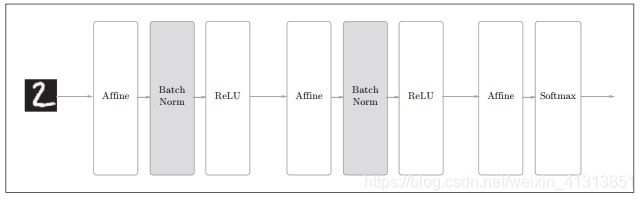
Batch Norm的思路时调整各层的激活值分布使其拥有适当的广度。而Batch Norm简单地说就是使数据分布的均值为0、方差为1的正规化。使用了Batch Norm的神经网络示意图如下所示。
2.Batch Normalization的评估
接下来对使用与不适用Batch Normalization算法进行对比,可以明显看出,使用了Batch Normalization算法后,学习进行得更快了。
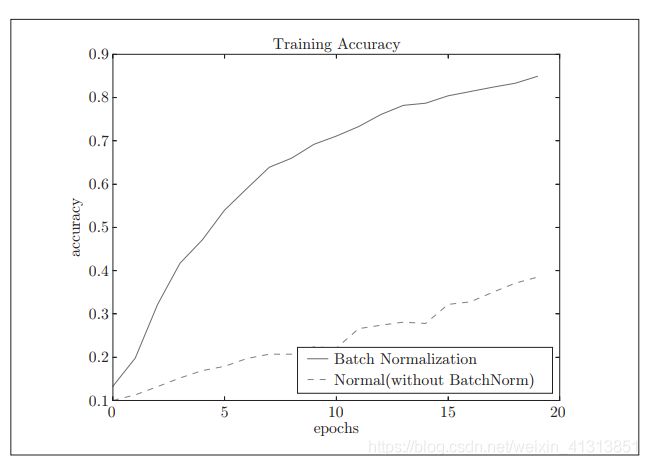
通常,几乎所有情况下都是使用了Batch Norm算法后学习进行的更快。且能够降低对初始值的依赖。
3.Batch Norm奏效的原因
为什么Batch归一化会起作用呢?一个原因是,通过归一化使得其均值为0,方差为1。我们可以看到我们经常会对输入的特征值 x x x进行归一化,可能将原本1到1000的特征值变成0到1.而Batch归一化也在做类似的工作,不仅仅针对输入值,还有隐藏层单元的值,能够较好的加速学习。其次,它可以使权重比你的网络更滞后或更深层。简单地说,较深的层次(例如第10层)相比于较前的层(例如第2层)更加能够经受得住变化。Batch归一化使得当输入值发生改变的情况下,中间隐层的变化变得更加小也更加稳定,即相当于当发生改变的时候,中间的隐层需要进行的适应与改变的程度减小了。它相当于减小了前层参数的作用与后层参数的作用之间的联系,使得网络层与层之间相对更加独立。
同时,Batch归一化还有轻微的正则化效果。因为在训练时,我们使用的每个mini batch计算出的方差和均值与整个数据集的方差和均值是有一定差异的,即存在一些小的噪声。所以Batch归一化相当于在每个隐藏层上增加了额外的噪声,使得后面的单元不会过分的依赖某一个隐层单元,因此有轻微的正则化效果。当然正则化绝不是Batch归一化的根本目的,你可以将其看作一个额外的惊喜。
参考文献
本文的参考内容有:
深度学习入门:基于Python的理论与实现
吴恩达老师的深度学习笔记(2017)