数值计算——线性最小二乘问题

数值计算——线性最小二乘问题

        最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

        m×n的线性方程组Ax=b是否有解？就是b能否表示成A的列向量的线性组合，当m=n时，肯定有解；当m>n，若b∈span(A)那么有解，否则无解。而对于线性最小二乘问题Ax＝b的解唯一的充要条件就是A列满秩，即rank(A)=n。用最小二乘法求解该方程就是使得残差向量r=b-Ax的二范数的平方取最小。

       这里使用正规方程组、QR分解两种方法求解线性最小二乘问题。

1、正规方程组

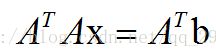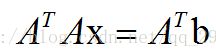      如果A列满秩，那么n×n正定对称正规方程组与m×n最小二乘问题Ax=b同解，求解该方程组则可通过楚列斯基分解法求得。理论上，有正规方程组可以得到线性最小二乘问题的精确解，但是由于正规方程组会出现条件数平方效应（叉积矩阵的条件数是原矩阵条件数的平方），所以往往得不到所期待的效果。

     代码实现也比较简单，只要求出A的转置、A的转置×A、A的转置×b就可以使用上一篇的楚列斯基分解求出方程的解了。

package com.kexin.lab4;

public class NomalEquation {
	/**
	 * Cholesky分解
	 * 
	 * @param a
	 * @return
	 */
	public static double[][] Cholesky(double[][] a) {
		int n = a.length;
		// 楚列斯基分解
		for (int k = 0; k < n; k++) {
			a[k][k] = Math.sqrt(a[k][k]);
			for (int i = k + 1; i < n; i++) {
				a[i][k] = a[i][k] / a[k][k];
			}
			for (int j = k + 1; j < n; j++) {
				for (int i = k + 1; i < n; i++) {
					a[i][j] = a[i][j] - a[i][k] * a[j][k];
				}
			}
		}
		return a;
	}

	/**
	 * 转置二维矩阵
	 * 
	 * @param a
	 * @return
	 */
	public static double[][] Transposition(double[][] a) {
		int m = a.length;
		int n = a[0].length;
		double[][] result = new double[n][m];
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				result[j][i] = a[i][j];
			}
		}
		return result;
	}

	/**
	 * 矩陣相乘
	 * 
	 * @param a
	 * @param a1
	 * @return
	 */
	public static double[][] MultiEquation(double[][] a, double[][] a1) {
		double[][] result = new double[a.length][a1[0].length];
		int x, i, j, tmp = 0;
		for (i = 0; i < a.length; i++) {
			for (j = 0; j < a1[0].length; j++) {
				for (x = 0; x < a1.length; x++) {
					tmp += a[i][x] * a1[x][j];// 矩阵AB中a_ij的值等于矩阵A的i行和矩阵B的j列的乘积之和
				}
				result[i][j] = tmp;
				tmp = 0; // 中间变量，每次使用后都得清零
			}
		}
		return result;
	}

	public static void main(String[] args) {
		// 输入方程系数矩阵A
		//double[][] a1 = { { 1, 0, 0 }, { 0, 1, 0 }, { 0, 0, 1 }, { -1, 1, 0 }, { -1, 0, 1 }, { 0, -1, 1 } };
//		double[][] a1 = {{0.16,0.10},{0.17,0.11},{2.02,1.29}};
		double[][] a1 = {{2,4},{3,-5},{1,2},{2,1}};
		double[][] a2 = Transposition(a1); // A的转置矩阵
		// 输入方程矩阵b
		//double[] b1 = { 1237, 1941, 2417, 711, 1177, 475 };
//		double[] b1 = {0.27,0.25,3.33};
		double[] b1 ={11,3,6,7};
		double[][] a = MultiEquation(a2, a1); // 系数矩阵的转置和系数矩阵的乘积n*n
		// 求解变化后的结果矩阵a2*b1
		int n = a2.length;
		int m = b1.length;
		double[] b = new double[n];
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				b[i] += a2[i][j] * b1[j];
			}
		}
		// 楚列斯基分解系数矩阵的转置和系数矩阵的乘积a
		Print2DArray("a", a);
		PrintArray("b", b);
		a = Cholesky(a);
		m = b.length;
		n = a.length;
		double x[] = new double[m];
		// 前代计算
		for (int j = 0; j < m; j++) {
			if (a[j][j] != 0) {
				x[j] = b[j] / a[j][j];
				b[j] = x[j];
			}
			for (int i = j + 1; i < m; i++) {
				b[i] = b[i] - a[i][j] * x[j];
			}
		}
		// 将a进行转置
		a = Transposition(a);
		// 回代计算
		for (int j = m - 1; j >= 0; j--) {
			if (a[j][j] != 0) {
				x[j] = b[j] / a[j][j];
			}
			for (int i = 0; i <= j - 1; i++) {
				b[i] = b[i] - a[i][j] * x[j];
			}
		}
		// 输出结果
		PrintArray("x", x);
	}
	/**
	 * 打印1D数组
	 * @param str
	 * @param result
	 */
	public static void PrintArray(String str, double[] result) {
		int n = result.length;
		System.out.print(str + "\n[");
		for (int i = 0; i < n; i++) {
			System.out.print(result[i] + "\t");
		}
		System.out.print(']');
		System.out.println();
		System.out.println();
	}
	/**
	 * 打印2D数组
	 * @param str
	 * @param result
	 */
	public static void Print2DArray(String str, double[][] result) {
		int n = result.length;
		int m = result[0].length;
		System.out.print(str + "\n");
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++)
				System.out.print(result[i][j] + "\t");
			System.out.println();
		}
		System.out.println();
	}
}

2、QR分解

      QR分解法是目前求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为Hessenberg矩阵，然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规正交矩阵的通用符号Q有关。

      计算矩阵QR分解的过程与用高斯消去法计算LU分解类似，都是在矩阵A中逐步引入零元素，使其具有上三角的形式。但这里用来约化的是正交阵（矩阵×矩阵的转置=单位阵），而不是初等消去阵，目的是保持2-范数不变。这类正交化的方法有很多，最常用的是豪斯霍尔德（Householder）变换。

package com.kexin.lab4;
/**
 * 使用豪斯霍尔德进行QR分解
 * @author KeXin
 *
 */
public class Householder {
	public static void main(String[] vd) {
		int i, j, k;
		// 初始化
		//double[][] a = { { 1, 0, 0 }, { 0, 1, 0 }, { 0, 0, 1 }, { -1, 1, 0 }, { -1, 0, 1 }, { 0, -1, 1 } };
		//double[] b = { 1237, 1941, 2417, 711, 1177, 475 };
//		double[][] a = {{0.16,0.10},{0.17,0.11},{2.02,1.29}};
//		double[] b = {0.26,0.28,3.31};
		double[][] a = {{2,4},{3,-5},{1,2},{2,1}};
		double[] b ={11,3,6,7};
		int m = a.length;
		int n = a[0].length;
		double sum, β = 0, γ = 0, x[] = new double[n];
		double v[] = new double[m];
		// 做HouseHolder转换
		for (k = 0; k < n; k++) {
			sum = 0;
			// 初始化v[]
			for (i = 0; i < k ; i++) {
				v[i] = 0;
			}
			for (i = k; i < m; i++) {
				v[i] = a[i][k];
			}
			// 求α
			for (j = k; j < m; j++) {
				sum = sum + a[j][k] * a[j][k];
			}
			// 处理符号
			if (a[k][k] >= 0) {
				sum = -Math.sqrt(sum);
			} else {
				sum = Math.sqrt(sum);
			}
			v[k] = v[k] - sum;
			β = 0;
			for (j = k; j < m; j++) {
				β = β + v[j] * v[j];
			}
			if (β == 0) {
				// donothing
			}
			for (j = k; j < n; j++) {
				γ = 0;
				for (i = k; i < m; i++) {
					γ = γ + v[i] * a[i][j];
				}
				for (i = k; i < m; i++) {
					a[i][j] = a[i][j] - (2 * γ / β) * v[i];
					if (Math.abs(a[i][j]) < 0.00001) {
						a[i][j] = 0;
					}
				}
			}
			double sumb = 0;
			for (i = k; i < m; i++) {
				sumb = sumb + b[i] * v[i];
			}
			for (i = 0; i < m; i++) {
				b[i] = b[i] - (2 * sumb / β) * v[i];
			}
		}
		Print2DArray("经HouseHolder变换后矩阵为：", a);
		PrintArray("矩阵b为：", b);
		// 回代计算
		for (i = n - 1; i >= 0; i--) {
			if (a[i][i] != 0) {
				x[i] = b[i] / a[i][i];
			}
			for (j = 0; j <=i-1; j++) {
				b[j] = b[j] - x[i] * a[j][i];
			}
		}
		PrintArray("矩阵x为：", x);
		double r = 0;
		for (i = m-1; i >= m/2; i--) {
			r = r + b[i] * b[i];
		}
		System.out.println("残差‖r‖为:" + r);
	}

	/**
	 * 打印1D数组
	 * 
	 * @param str
	 * @param result
	 */
	public static void PrintArray(String str, double[] result) {
		int n = result.length;
		System.out.print(str + "\n[");
		for (int i = 0; i < n; i++) {
			System.out.print(Math.round(result[i]) + "\t");
		}
		System.out.print(']');
		System.out.println();
		System.out.println();
	}

	/**
	 * 打印2D数组
	 * 
	 * @param str
	 * @param result
	 */
	public static void Print2DArray(String str, double[][] result) {
		int n = result.length;
		int m = result[0].length;
		System.out.print(str + "\n");
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++)
				System.out.print(result[i][j] + "\t");
			System.out.println();
		}
		System.out.println();
	}
}