COI实验室技能:常见的图像增强算法(含MATLAB代码)
成像系统采集到的图片有时不一定具有很好的图像质量,往往需要进行一些图像增强的操作。本文主要整理了几种常见的图像增强算法,包括:同态滤波、CLAHE、Retinex、导向滤波、全局低照度增强等等。这些图像增强算法可以改变图像的对比度分布,使得图像视觉效果更好。下面将给出每个算法的简介及其matlab代码,以帮助读者能快速复现相关算法,篇幅较长,读者可以根据自己需求选读。
笔者主要研究散射成像,由散射介质引起的退化图像往往具有很低的对比度,下面给出不同增强方法的对比结果:
对于不同的方法,读者可以理解其基本思路,掌握不同的函数参数对结果的影响,进而可以根据实际需要适当调整参数。
目录
- 1. 同态滤波
- 2. CLAHE
- 3. Retinex
- 4. 基于导向滤波的HDR
- 5. 全局低照度增强
- 6. 结论
1. 同态滤波
使用场景:图像阴影区域的细节看不清楚,通过对数变化和福
同态滤波利用对数变换分离信号中的乘性成分,进而通过线性滤波(主要是频域滤波)的手段对特定的信号进行处理;比如将图像解析为照度分量和物体反射分量的乘积,通过照度分量和物体分量在频域上的差异,设计特定的滤波器(如巴特沃斯高通滤波器)实现低频分量的抑制和高频分量的增强,从而同时增加对比度以及标准化亮度, 实现图像增强的目的。
如上图所示,其基本操作流程为:
① 对图像进行对数变换;
② 对变换后的图像进行傅里叶变换,此时乘性的图像分量在频域空间上是分离的;
③ 目的是抑制低频分量,增强高频分量,因此采用高通滤波器,同时不能完全消除低频的能量,因此必须抬高高通滤波的最低值,因此常常采用如下形式的高通滤波器:
H ( u , v ) = ( r H − r L ) H h p ( u , v ) + r L H(u,v) = ({r_H} - {r_L}){H_{hp}}(u,v) + {r_L} H(u,v)=(rH−rL)Hhp(u,v)+rL 其中:
r H , r L r_H,r_L rH,rL表示滤波器的上下界;
H ( u , v ) H(u,v) H(u,v)表示同态滤波使用的调整之后的高通滤波器;
H h p ( u , v ) H_{hp}(u,v) Hhp(u,v)可以使用高斯高通滤波器、巴特沃兹高通滤波器等等;
如果选用高斯低通滤波器,则 H h p ( u , v ) H_{hp}(u,v) Hhp(u,v)为:
H h p ( u , v ) = 1 − exp [ − c ( D 2 ( u , v ) / D 0 2 ) ] H_{hp}(u,v) = 1-\exp[{-c(D^2(u,v)/D^2_0)}] Hhp(u,v)=1−exp[−c(D2(u,v)/D02)] c c c表示高斯函数的陡峭程度;
D 0 D_0 D0表示高斯函数的标准差,控制着区分高频和低频的界限;
此时,同态滤波的高通滤波器为: H ( u , v ) = ( r H − r L ) { 1 − exp [ − c ( D 2 ( u , v ) / D 0 2 ) ] } + r L H(u,v) = ({r_H} - {r_L})\{1-\exp[{-c(D^2(u,v)/D^2_0)}]\}+ {r_L} H(u,v)=(rH−rL){1−exp[−c(D2(u,v)/D02)]}+rL 参考资料:
同态滤波及其实现(https://blog.csdn.net/cjsh_123456/article/details/79351654)
同态滤波原理及其matlab实现(https://zhuanlan.zhihu.com/p/332905808)
结合上述的原理,同态滤波的matlab实现代码如下:
clc,clear
close all;
image1 = im2double(imread('img.png'));
image2 = HomoFilter(image1, 2, 0.25, 1, 80); % (img, rh, rl, c, D0)
% 显示图像
subplot(1,2,1), imshow(image1), title('原图像');
subplot(1,2,2), imshow(image2), title('D0 = 80');
其中HomoFilter函数定义如下:
function [image_out] = HomoFilter(image_in, rh, rl, c, D0)
% 同态滤波器
% 输入为需要进行滤波的灰度图像,同态滤波器的参数rh, rl,c, D0
% 输出为进行滤波之后的灰度图像
[m, n] = size(image_in);
P = 2*m;
Q = 2*n;
% 取对数
image1 = log(double(image_in) + 1);
fp = zeros(P, Q);
%对图像填充0,并且乘以(-1)^(x+y) 以移到变换中心
for i = 1 : m
for j = 1 : n
fp(i, j) = double(image1(i, j)) * (-1)^(i+j);
end
end
% 对填充后的图像进行傅里叶变换
F1 = fft2(fp);
% 生成同态滤波函数,中心在(m+1,n+1)
Homo = zeros(P, Q);
a = D0^2; % 计算一些不变的中间参数
r = rh-rl;
for u = 1 : P
for v = 1 : Q
temp = (u-(m+1.0))^2 + (v-(n+1.0))^2;
Homo(u, v) = r * (1-exp((-c)*(temp/a))) + rl;
end
end
%进行滤波
G = F1 .* Homo;
% 反傅里叶变换
gp = ifft2(G);
% 处理得到的图像
image_out = zeros(m, n, 'uint8');
gp = real(gp);
g = zeros(m, n);
for i = 1 : m
for j = 1 : n
g(i, j) = gp(i, j) * (-1)^(i+j);
end
end
% 指数处理
ge = exp(g)-1;
% 归一化到[0, L-1]
image_out = im2uint8(mat2gray(ge)); % 先归一化到0-1,在转为uint8类型;
end
运行结果:
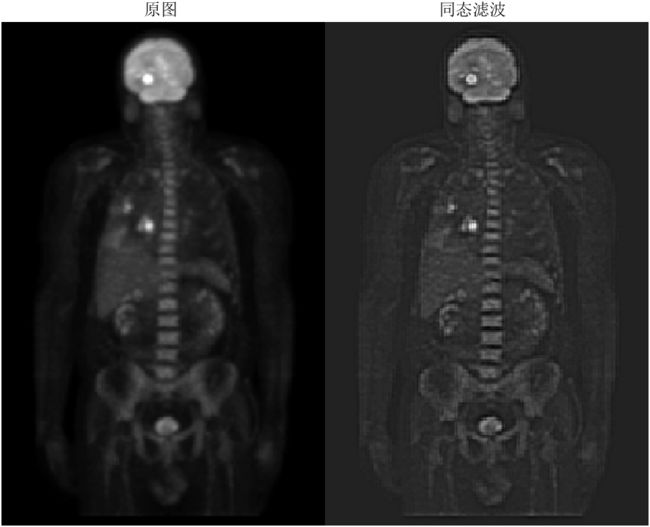
如图,经过同态滤波处理后的图像阴影区域的细节更加清楚了。
尝试用同态滤波处理其他图片,注意不同的图片处理效果需要适当的调整函数参数,彩色处理的处理笔者是将图像变换为HSV格式后,对强度分量进行同态滤波,再变回RGB图像。

2. CLAHE
直方图均衡化模型
原本图像的直方图分布为: f X ( x ) f_X(x) fX(x),为了使得变换后的图像 y = T ( x ) y=T(x) y=T(x)的直方图 f Y ( y ) f_Y(y) fY(y)满足均衡化分布,即 f Y ( y ) = 1 / 255 f_Y(y)=1/255 fY(y)=1/255,直方图均衡化模型为:
y = 255 ∗ ∑ i = 1 x f X ( i ) y=255* \sum_{i=1}^{x}f_X(i) y=255∗i=1∑xfX(i)对比度受限的自适应直方图均衡化
CLAHE是一种用于提高图像对比的数字图像处理技术。它与普通直方图均衡化的不同之处在于自适应方法计算多个直方图,每个直方图对应于图像的不同部分,并使用这些直方图重新分配图像的亮度值。因此,它适用于提高局部对比度和增强图像每个区域的边缘清晰度[来源与wiki]。
CLAHE具体实现主要包括6个步骤。
步骤1:分块。将输入图像划分为大小相等的不重叠子块,每个子块含有的像素数为M。参考示例为8×8块。
步骤2:计算子块直方图。
步骤3:计算剪切阈值clipLimit(可以展开讨论)
步骤4:像素点重分配。对每个子块,使用步骤三中多余的像素重新分配。
步骤5:直方图均衡。
步骤6:像素点灰度值重构。(源码中采用了双线性插值)
参考资料:
clahe(限制对比度自适应直方图均衡化);
基于直方图的图像增强算法(HE、CLAHE)之(二);
matlab的adapthisteq函数;
代码实现:
matlab实现CLAHE的函数是:
img_clahe = adapthisteq(img, 'name', 'value');
数据类型: single | double | int16 | uint8 | uint16
| 名称 | 说明 |
|---|---|
| NumTiles | 图块数量,[8,8] (默认) |
| ClipLimit | 对比度增强限制,0.01 (默认) |
| NBins | 用于构建对比度增强变换的直方图 bin 数,256 (默认) |
| Range | 输出数据的范围,‘full’ (默认) |
| Distribution | 对比度增强限制,0.01 (默认) |
程序:
clc, clear
close all
% 读取图片
img = imread('./img.png');
img_lab = rgb2lab(img);
% 对比度拉伸
img_lab(:,:,1) = 100*adapthisteq(img_lab(:,:,1)/100);
img_clahe = lab2rgb(img_lab);
imshowpair(img,img_clahe,'montage');
运行结果:

经验:在对彩色图像进行对比度增强时,有三种方法可以使用adapthisteq,一是分别对三个彩色通道进行对比度拉伸后再合并,二是将彩色图像转换为HSV图像后,再对V通道进行增强,三是将彩色图像转换为LAB图像后,在对L通道进行增强,通过对比可得,增强效果以及颜色失真较少的方式是转换为LAB格式后再增强的效果。
不同彩色图像增强处理方法结果对比:
对雾图的处理结果:

city雾图的处理结果:

如图所示,从不同图像的测试结果可以发现,仅仅靠直方图均衡化,处理结果很不理想(模型本身没有考虑图像中透射率分布不均匀的情况),对于具体的图像处理任务应该考虑好任务的特点,不能盲目地直接使用某一种方法。
3. Retinex
参考资料:Retinex图像增强算法理论基础
主要解决问题:图像存在光照不均匀的问题、图像对比度低的问题;
基本思想是人感知到某点的颜色和亮度并不仅仅取决于该点进入人眼的绝对光线, 还和其周围的颜色和亮度有关。
Retinex 理论的基本内容是物体的颜色是由物体对长波(红)、中波(绿)和短波(蓝)光线的反射能力决定的,而不是由反射光强度的绝对值决定的;在照明光谱一致的情况下,物体的色彩不受光照非均性的影响,具有一致性,即 Retinex 理论是以色感一致性(颜色恒常性)为基础的。
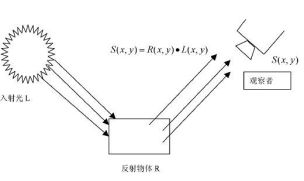
Retinex理论的基本假设是原始图像S是光照图像L和反射率图像R的乘积,即可表示为下式的形式:
S ( x , y ) = R ( x , y ) ⋅ L ( x , y ) S(x,y)=R(x,y){\cdot}L(x,y) S(x,y)=R(x,y)⋅L(x,y)基于Retinex的图像增强的目的就是从原始图像S中估计出光照L,从而分解出R,消除光照不均的影响,以改善图像的视觉效果,正如人类视觉系统那样。在处理中,通常图像转至对数域,处理思路与同态滤波的相似,即 s = log S , l = log L , r = log R s={\log}S, l={\log}L, r={\log}R s=logS,l=logL,r=logR,从而将乘积关系转换为和的关系:
s = log S = log R ⋅ L = log R + log L = s + l s={\log}S={\log}R{\cdot}L={\log}R+{\log}L=s+l s=logS=logR⋅L=logR+logL=s+lRetinex方法的核心就是估测照度L, 从图像S中估测L分量,并去除L分量,得到原始反射分量R,即:
l = f ( s ) , r = s − f ( s ) l=f(s), r=s-f(s) l=f(s),r=s−f(s)函数 f ( s ) f(s) f(s)实现对照度L的估计(可以按照这个模式去理解,不过实际很多时候都是直接估计分量r)。
与降噪类似,该理论的关键就是合理地假设了图像的构成。如果将观察者看到的图像看成是一幅带有乘性噪声的图像,那么入射光的分量就是一种乘性的,相对均匀,且变换缓慢的噪声。Retinex 算法所做的就是合理地估计图像中各个位置的噪声,并除去它;除了Retinex,其改进算法还有多尺度融合的retinex算法(MSR,加权多个不同sigma的结果),色彩复原的多尺度融合retinex算法(MSRCR)等等,这里受限篇幅和精力,仅给出单尺度的retinex算法参考程序。
处理流程:高斯滤波、对数与反对数Map以及图像拉伸算法。高斯滤波主要消除高频成分,得到图像的本底起伏(近似为不均匀的照明光),原图log减去本底log得到场景反射分量(近似认为是消除了光照不均性之后的结果),去指数还原到空间域,再通过对比度拉伸算法得到retinex算法的结果。
SSR的参考程序:
clc;
clear;
img=imread('./test images/under_water.jpg');%读入图片
sigma=250; % 高斯滤波器的标准差,可适当调整
if size(img,3)>1 % 处理彩色图像
for k=1:3
R=img(:,:,k);
[N1,M1]=size(R);
F=zeros(N1,M1);%定义高斯滤波函数
for i=1:N1
for j=1:M1
F(i,j)=exp(-((i-N1/2)^2+(j-M1/2)^2)/(2*sigma*sigma));
end
end
F = F./(sum(F(:)));
R0=double(R);%R信道
Rlog=log(R0+1);%取对数
Rfft2=fft2(R0);%傅立叶二维
Ffft2=fft2(double(F));%高斯滤波二维傅立叶
DR0=Rfft2.*Ffft2;%频率域高斯滤波
DR=ifft2(DR0);%滤波后空间对数域图像
DRdouble=double(DR);
DRlog=log(DRdouble+1);%相减得到高频部分
Rr=Rlog-DRlog;
EXPRr=exp(Rr);
MIN = min(min(EXPRr));
MAX = max(max(EXPRr));
EXPRr = (EXPRr-MIN)/(MAX-MIN);
EXPRr=adapthisteq(EXPRr);
I0(:,:,k)=EXPRr;
end
else % 处理灰度图像
R=img;
[N1,M1]=size(R);
F=zeros(N1,M1);%定义高斯滤波函数
for i=1:N1
for j=1:M1
F(i,j)=exp(-((i-N1/2)^2+(j-M1/2)^2)/(2*sigma*sigma));
end
end
F = F./(sum(F(:)));
R0=double(R);%R信道
Rlog=log(R0+1);%取对数
Rfft2=fft2(R0);%傅立叶二维
Ffft2=fft2(double(F));%高斯滤波二维傅立叶
DR0=Rfft2.*Ffft2;%频率域高斯滤波
DR=ifft2(DR0);%滤波后空间对数域图像
DRdouble=double(DR);
DRlog=log(DRdouble+1);%相减得到高频部分
Rr=Rlog-DRlog;
EXPRr=exp(Rr);
MIN = min(min(EXPRr));
MAX = max(max(EXPRr));
EXPRr = (EXPRr-MIN)/(MAX-MIN);
EXPRr=adapthisteq(EXPRr);
I0=EXPRr;
end
%%%
subplot(121),imshow(img), title('原图');
subplot(122),imshow(I0), title('Retinex');
4. 基于导向滤波的HDR
参考资料:何凯明guided filtering主页
图像处理基础(一)引导滤波
导向滤波(Guided Filter)的解析与实现

如图所示的是导向滤波的基本原理图,p是需要滤波的图像,I是引导图像(可以是自身或者其他图片),当I是自身p时,滤波结果为边缘保留的去噪平滑效果;
一方面,利用引导图来计算窗口的局部线性系数,这一特性使得窗口的权重根据图像的梯度信息而变化,在平滑区域有均值滤波的效果,在边缘区域可以保留边缘法向的梯度信息;另一方面,将局部线性变化的结果与输入图像取均方差,使得滤波后的图像拥有真实图像的约束。提示,本文所述的原理过于简略,建议读者阅读上述的参考资料来理解原理。在guide filter原理中,定义目标函数为:
min E ( a k , b k ) = ∑ i ∈ w k ( ( a k I i + b k − p i ) 2 + ε a k 2 ) {\min}\ \ E(a_k,b_k) = \sum_{i\in w_k}((a_kI_i+b_k-p_i)^2+{\varepsilon}a_k^2) min E(ak,bk)=i∈wk∑((akIi+bk−pi)2+εak2)该方程为线性岭回归模型,其最优解为:
a k = { 1 ∣ w ∣ ∑ i ∈ w k I i p i − u k p ‾ k σ k 2 + ε } , a_k=\{\frac{{\frac{1}{|w|}\sum_{i\in w_k}I_ip_i-u_k\overline p_k}}{{\sigma _k^2+\varepsilon}}\}, ak={σk2+ε∣w∣1∑i∈wkIipi−ukpk}, b k = p ‾ k − a k u k . b_k=\overline p_k-a_ku_k. bk=pk−akuk.求解出 a k , b k a_k,b_k ak,bk之后,对于某一像素点 i i i, 在 w k w_k wk窗口内有多个不同的结果,文章的处理办法是求出所有 q i q_i qi再取平均:
q i = 1 ∣ w ∣ ∑ k ∣ i ∈ w k ( a k I i + b k ) . q_i=\frac {1}{|w|}\sum_{k|i\in w_k}(a_kI_i+b_k). qi=∣w∣1k∣i∈wk∑(akIi+bk).根据方形窗口的几何特性,我们可以将上式写为: q i = a ‾ i I i + b ‾ i q_i=\overline a_iI_i+\overline b_i qi=aiIi+bi整理guide filtering的流程为:

参考代码:
首先需要定义guidedfilter、boxfilter函数,然后编写脚本调用它们,以实现引导滤波。
main函数:读取图像 -> 对图像进行增强且增加适当的噪声 -> 以自身为引导图实现保边缘滤波 -> 显示图像。
clc, clear
close all
% 读取图片
filename = '../test images/woman.png';
img = (imadjust(adapthisteq(im2double(imread(filename))+randn(640,640)*0.01)));
img1 = guidedfilter(img,img,3,0.04);
imshow([img img1],[]);
声明:函数代码来自Dr. kaiming He。
在guidedfilter函数中I是引导图像,p滤波输入图像,r控制窗口大小,eps为正则化系数 ε \varepsilon ε。
guidedfilter函数:
function q = guidedfilter(I, p, r, eps)
% - guidance image: I (should be a gray-scale/single channel image)
% - filtering input image: p (should be a gray-scale/single channel image)
% - local window radius: r
% - regularization parameter: eps
[hei, wid] = size(I);
N = boxfilter(ones(hei, wid), r);
mean_I = boxfilter(I, r) ./ N;
mean_p = boxfilter(p, r) ./ N;
mean_Ip = boxfilter(I.*p, r) ./ N;
% this is the covariance of (I, p) in each local patch.
cov_Ip = mean_Ip - mean_I .* mean_p;
mean_II = boxfilter(I.*I, r) ./ N;
var_I = mean_II - mean_I .* mean_I;
a = cov_Ip ./ (var_I + eps);
b = mean_p - a .* mean_I;
mean_a = boxfilter(a, r) ./ N;
mean_b = boxfilter(b, r) ./ N;
q = mean_a .* I + mean_b;
end
boxfilter函数:
function imDst = boxfilter(imSrc, r)
% BOXFILTER O(1) time box filtering using cumulative sum
%
% - Definition imDst(x, y)=sum(sum(imSrc(x-r:x+r,y-r:y+r)));
% - Running time independent of r;
% - Equivalent to the function: colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
% - But much faster.
[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));
%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);
%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);
end
去噪结果:
 如图,可以观察到人物背后的指示牌仍保留着清晰的轮廓。
如图,可以观察到人物背后的指示牌仍保留着清晰的轮廓。
导引滤波实现HDR,待补充。
5. 全局低照度增强
问题描述:解决彩色图像中有部分区域照度很低的问题;
参考资料:简单有效的低照度增强
文献:《Adaptive and integrated neighborhood-dependent approach for nonlinear enhancement of color images》
算法基本流程:
- 根据图像的亮度分布建立一个全局映射;
- 自适应对比度增强;
- 颜色恢复;
全局曲线调整:
- 利用MATLAB的rgb2gray函数求解彩色图像的亮度值(灰度值):I = rgb2gray(I);
- 灰度图像进行归一化:I = im2double(I);
- 利用映射函数对图像进行强度变换;
a = 0.24 , b = 0.5 a=0.24,b=0.5 a=0.24,b=0.5 I n ( x , y ) = I ( x , y ) a + ( 1 − I ( x , y ) ) b + I ( x , y ) 2 2 I_n(x,y)=\frac {I(x,y)^a + (1-I(x,y))^b+I(x,y)^2}{2} In(x,y)=2I(x,y)a+(1−I(x,y))b+I(x,y)2
关于为什么要采用该映射函数,笔者利用该函数画出了它对不同强度的变换结果: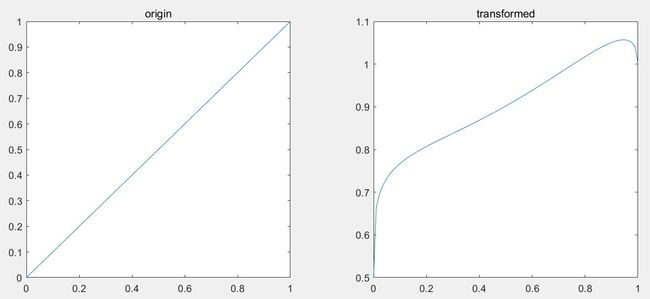 如图所示,变换后的曲线低照度(低强度)的数值被提升到了0.7以上,而右侧的高强度区域则变化不大,从而增强了低照度区域的强度,再结合对比度拉伸算法,就可以改善图像的显示效果。
如图所示,变换后的曲线低照度(低强度)的数值被提升到了0.7以上,而右侧的高强度区域则变化不大,从而增强了低照度区域的强度,再结合对比度拉伸算法,就可以改善图像的显示效果。
对比度增强:
- 对 I ( x , y ) I(x,y) I(x,y)进行不同尺度的高斯滤波,定义高斯函数为:
G ( x , y ) = K ⋅ e ( − ( x 2 + y 2 ) σ 2 ) G(x,y)=K\cdot e(\frac {-(x^2+y^2)}{\sigma ^2}) G(x,y)=K⋅e(σ2−(x2+y2)) σ \sigma σ为高斯函数标准差(尺度),同时定义窗口大小为 [ 2 σ + 1 , 2 σ + 1 ] [2\sigma+1,2\sigma+1] [2σ+1,2σ+1],取 σ = 5 , 20 , 240 \sigma=5,20,240 σ=5,20,240,求出不同尺度的卷积结果: I g i ( x , y ) = I ( x , y ) ∗ G i ( x , y ) I_{gi}(x,y)=I(x,y)*G_i(x,y) Igi(x,y)=I(x,y)∗Gi(x,y) - 对比度增强
r i ( x , y ) = I g i ( x , y ) I ( x , y ) r_i(x,y)=\frac{I_{gi}(x,y)}{I(x,y)} ri(x,y)=I(x,y)Igi(x,y) R i ( x , y ) = I n ( x , y ) r i ( x , y ) R_i(x,y)=I_n(x,y)^{r_i(x,y)} Ri(x,y)=In(x,y)ri(x,y) 对于相对较暗的像素,经过高斯滤波后其像素值比原来的大,此时 r i r_i ri大于1,该像素点(注意I已经归一化,数值都小于1)次方之后像素值将更暗,而对于原本较亮的像素,高斯滤波后像素值下降, r i r_i ri小于1,次方之后像素值更大,因此可以得到对比度拉伸的效果。 - 不同尺度增强因子线性结合:
R ( x , y ) = 1 3 ∑ i 3 R i ( x , y ) R(x,y)=\frac{1}{3}\sum_i^3{R_i(x,y)} R(x,y)=31i∑3Ri(x,y)不同的尺度考虑了不同邻域大小的情况。
颜色复原:
R j ( x , y ) = I j ( x , y ) I n ( x , y ) ,其中 j 为 r , g , b 三通道 R_j(x,y)=\frac{I_j(x,y)}{I_n(x,y)},其中j为r,g,b三通道 Rj(x,y)=In(x,y)Ij(x,y),其中j为r,g,b三通道代码实现:
I=im2double(imread('city.jpg'));
I1=rgb2gray(I);
In=(I1.^(0.24)+(1-I1).*0.5+I1.^2)/2;
%通过高斯核对灰度增强图像做卷积运算
sigma=5;
window = double(uint8(3*sigma)*2 + 1);
G1=fspecial('gaussian',window,sigma);
Guass1=imfilter(I1,G1,'conv','replicate','same');
r1=Guass1./I1;
R1=In.^r1;
sigma=20;
window = double(uint8(3*sigma)*2 + 1);
G2=fspecial('gaussian',window,sigma);
Guass2=imfilter(I1,G2,'conv','replicate','same');
r2=Guass2./I1;
R2=In.^r2;
sigma=240;
window = double(uint8(3*sigma)*2 + 1);
G3=fspecial('gaussian',window,sigma);
Guass3=imfilter(I1,G3,'conv','replicate','same');
r3=Guass3./I1;
R3=In.^r3;
R=(R1+R2+R3)/3;
Rr=R.*(I(:,:,1)./I1);
Rg=R.*(I(:,:,2)./I1);
Rb=R.*(I(:,:,3)./I1);
rgb=cat(3,Rr,Rg,Rb);
imshow([I rgb]);
增强结果:

如图所示,图中左下角和右下角照度低的区域得到了增强,实现了全局低照度增强的目的。
6. 结论
本文整理了提升图像对比度和图像质量的几种常见方法——同态滤波、CLAHE、Retinex、引导滤波、全局低照度增强等等,简单介绍了它们的基本原理,如果要更为深刻的掌握,需要读者阅读文献原文以及自己多用代码复现。在未来提出新的方法时,可以与传统的图像增强算法进行对比,以此更充分地验证自己的方法。
文章声明
编辑:王浩帆、刘海山
单位:中国科学院上海光学精密机械研究所,司徒国海课题组(计算光学成像)
欢迎各位读者学习交流,指正不足!

