曲线拟合的数值方法——《数值计算方法》

《数值计算方法》系列总目录

第一章 误差序列实验
第二章 非线性方程f(x)=0求根的数值方法
第三章 CAD模型旋转和AX=B的数值方法
第四章 插值与多项式逼近的数值计算方法
第五章 曲线拟合的数值方法
第六章 数值微分计算方法
第七章 数值积分计算方法
第八章 数值优化方法

---

---

一、算法原理

1、最小二乘拟合曲线

  在科学和工程试验中,经常产生一组数据($x_1,y_1$),…,($x_N,y_N$),这里的横坐标{$x_k$}是明确的的。数值方法的目标之一是确定一个将这些变量联系起来的函数$y=f(x)$，即通过算法形成一种数学刻画的公式来寻求其中的规律。通常会选择一类可用的函数并确定它们的系数，然而这类函数不是随便选取的，必须根据实际的实验数据进行判断，选取最符合的函数模型，因此选择函数的可能性是多种多样的。一般会根据物理情况采用一个基本数学模型来确定函数的形式。这一节主要分析线性函数,其形式为
$$y=f(x)=Ax+B$$  根据插值多项式逼近原理，如果所有的数值{$x_k$},{$y_k$}已知有多位有效数字精度,则能成功地使用多项式插值;否则,不能使用多项式插值。因为插值多项式是根据已有的精确的实验数据进行多项式拟合的，其拟合结果一定会经过插值点，如果插值点数据本身存在较大误差，则逼近结果就会出现更大误差。然而,许多试验数据可能并没有如此高的精度,而且通常在试验中还存在试验误差,所以尽管记录的{$x_k$},{$y_k$}有多位有效数字,但还是与其真实值存在范围外的误差，即真实值$f(x_k)$满足$f(x_k)=y_k+e_k$，其中，$e_k$表示测量误差，因此需要寻找一种经过测试点附近(不总是穿过)的最佳线性逼近表达式。下面首先对误差(又称偏差或残差)概念进行一个介绍：
$$e_k=f(x_k)-y_k,for1\le k\le N$$  其中，$y_k$测量实验值，$f(x_k)$表示真实值，误差还有其他表示如下形式：
$$E_{\infty }(f)=\underset{1\le k\le N}{\max }\{|f(x_k)-y_k|\}$$$$E_1(f)=\frac{1}{N}\sum _{k=1}^N\left|f(x_k)-y_k\right|$$$$E_2(f)={\left(\frac{1}{N}\sum _{k=1}^N{\left|f(x_k)-y_k\right|}^2\right)}^{1/2}$$  那么如何确定系数$A，B$使得曲线拟合达到我们想要的效果呢？其中，最小二乘法是在进行曲线拟合时常用的一种求解拟合曲线表达式的方法，无论是拟合何种曲线，其系数求解基本思想都是基于最小二乘法的。分析可知，设 是一个N个点的集合，其中横坐标是确定的。那么，理想的最小二乘拟合曲线 的拟合结果应满足是均方根误差最小的曲线。那么，所选定的$A，B$构成的拟合曲线应当使$E_2(f)$的值当且仅当所选取的$A，B$值处最小。换言之，也就是说数据点到曲线的垂直距离平方和最小，即误差的平方和，其最小值为$N(E_2(f{)}^2)=\sum _{k=1}^N{\left|A{x}_k+B-y_k\right|}^2$。那么，基于实验结果的所求出选取$A，B$的值的表达式到底是怎样的呢？因此，有如下推导过程：
  设$\{(x_k,y_k){\}}_{k=1}^N$有N个点，其中横坐标是确定的，当数据点到曲线的垂直距离平方和最小时，$A，B$取值点应在误差表达式的极值处，即表达式对于$A，B$两变量的偏导数为0，即
$$\begin{gathered} \frac{\partial E(A,B)}{\partial A}=\sum _{k=1}^{N}2\left(A{x}_k+B-y_k\right)x_k=0 \\ \frac{\partial E(A,B)}{\partial B}=\sum _{k=1}^{N}2\left(A{x}_k+B-y_k\right)=0 \end{gathered}$$  通过移项变换即得到关于系数$A，B$的表达式如下
$$\begin{gathered} \left(\sum _{k=1}^N{x}_k^2\right)A+\left(\sum _{k=1}^N{x}_k^{}\right)B=\sum _{k=1}^N{x}_k{y}_k \\ \left(\sum _{k=1}^N{x}_k^{}\right)A+NB=\sum _{k=1}^N{y}_k \end{gathered}$$  并称式（5）表示的方程组为正规方程。得到的曲线称为最小二乘拟合曲线。
  除此之外，对于形如$f(x)=A{x}^M$幂函数拟合，其中M为已知常数，根据线性曲线的拟合推导过程，写出幂函数数据点到曲线的垂直距离平方和表达式，即
$$E(A)=\sum _{k=1}^N{\left(A{x}_k^M-y_k\right)}^2$$  求出A为其极小值点时候的值，即表达式对于A的偏导数为0，即
$$E^{\prime }(A)=2\sum _{k=1}^N\left(A{x}_k^M-y_k\right)x_k^M=2\sum _{k=1}^N\left(A{x}_k^{2M}-x_k^M{y}_k\right)=0$$  最终可以得出幂函数拟合曲线的系数A的表达式为

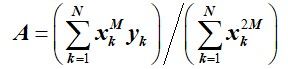
2、曲线拟合原理

  对于不是线性关系的曲线拟合，可以对其进行线性化操作再利用最小二乘法求出其系数的表达式即可。也就是说，对于一组不具有线性关系的数据点集合，可以对其进行诸如取对数、指数的方法将其变换为具有线性关系的表达式，即将数据点$xk,yk$变换成$XY$平面上具有线性关系的点集$Xk,Yk$,再利用最小二乘法求出变换后的曲线表达式，最后再变换为原变量的表达式。这个过程称为数据线性化。例如，对于非线性函数[y = C{e^{Ax}}]，可以对其进行取对数变化，即
$$\ln (y)=Ax+\ln (C)$$  并引入变量， ，得到变换后的线性关系式 ，根据最小二乘法的结果，系数$A，B$表达式为
$$\begin{gathered} \left(\sum _{k=1}^N{X}_k^2\right)A+\left(\sum _{k=1}^N{X}_k^{}\right)B=\sum _{k=1}^N{X}_k{Y}_k \\ \left(\sum _{k=1}^N{X}_k^{}\right)A+NB=\sum _{k=1}^N{Y}_k \end{gathered}$$$$C=e^B$$  则可以得到拟合曲线的表达式。然而，也可以直接写出数据点到曲线的垂直距离平方和表达式，并求出其极值点，即为拟合曲线的系数表达式，其推导过程如下：
$$\begin{gathered} E(A,C)=\sum _{k=1}^N{\left(C{e}^{A{x}_k}-y_k\right)}^2 \\ \mathrm{l}\mathrm{e}\mathrm{t}\{\begin{array}{l}\frac{\partial E}{\partial A}=2\sum _{k=1}^N\left(C{e}^{A{x}_k}-y_k\right)\left(C{x}_k{e}^{A{x}_k}\right)=0\\ \frac{\partial E}{\partial C}=2\sum _{k=1}^N\left(C{e}^{A{x}_k}-y_k\right)\left(e^{A{x}_k}\right)\end{array} \\ \mathrm{s}\mathrm{o} \\ \{\begin{array}{l}C\sum _{k=1}^N{x}_k{e}^{2A{x}_k}-\sum _{k=1}^N{y}_k{x}_k{e}^{A{x}_k}=0\\ C\sum _{k=1}^N{e}^{A{x}_k}-\sum _{k=1}^N{y}_k{e}^{A{x}_k}=0\end{array} \end{gathered}$$  其中未知数$A，C$是非线性的，可用牛顿法求解，可以看出，直接利用最小二乘法求解更加复杂。除此之外，在求解其他函数的拟合曲线的时候，也可以进行类似的数据线性变换。具体如下图所示。

  除此之外，还可以使用线性最小二乘法来进行拟合。即设有N个数据点$\{(x_k,y_k)\}$，并给定了M个线性独立的函数$f_i(x)$。利用这些线性独立的函数的线性组合表示函数$f(x)$，即
$$f(x)=\sum _{j=1}^M{c}_j{f}_j(x)$$  同样，利用最小二乘法求解系数的思想，使其数据点到曲线的垂直距离平方和最小，即其表达式对于每一个参数$c_i$的偏导数为0，则可以得到其正规方程：
$$\sum _{j=1}^M\left(\sum _{k=1}^N{f}_i(x_k)f_j(x_k)\right)c_j=\sum _{k=1}^N{f}_i(x_k)y_k,i=1,2,...,M$$  不难看出，等式左边可以表达为矩阵乘积的结果，因此构造如下矩阵：

  则等式右边可以写成如下形式

  而方程左边未知参数c的系数可以写为矩阵F与其逆矩阵的乘积，因此，方程组可以表达为如下线性方程组的形式：
$$F^{\prime }FC=F^{\prime }Y$$  对于不太大的M，可以利用第三章求解线性方程组的方法求解系数c，从而得出函数的表达式。因此，当所取线性独立函数$f_i(x)$为幂函数时，则函数$f(x)$可以表示为M阶多项式的形式，然而事实上，这种多项式拟合通常具有多项式摆动的特性，因此会造成拟合结果的失真，而且阶数越高越容易发生，因此通常情况下只会取到二阶多项式进行拟合，除非已知使用的多项式是真实的。因此，进行最小二乘抛物线拟合的函数表达式为
$$y=f(x)=C+Bx+A{x}^2$$  同样，利用最小二乘法求解系数的思想，使其数据点到曲线的垂直距离平方和最小，即其表达式对于每一个参数的偏导数为0，则可以得到其正规方程：
$$\begin{gathered} \left(\sum _{k=1}^N{x}_k^4\right)A+\left(\sum _{k=1}^N{x}_k^3\right)B+\left(\sum _{k=1}^N{x}_k^2\right)C=\sum _{k=1}^N{y}_k{x}_k^2 \\ \left(\sum _{k=1}^N{x}_k^3\right)A+\left(\sum _{k=1}^N{x}_k^2\right)B+\left(\sum _{k=1}^N{x}_k^{}\right)C=\sum _{k=1}^N{y}_k{x}_k^{} \\ \left(\sum _{k=1}^N{x}_k^2\right)A+\left(\sum _{k=1}^N{x}_k^{}\right)B+NC=\sum _{k=1}^N{y}_k \end{gathered}$$  以上系数表达式即为进行二阶多项式拟合的各阶项系数表达式。

3、样条插值

  对N+1个点 的多项式插值经常不令人满意。一个N阶多项式可能有N-1个相对极大值和极小值,同时曲线可能会摆动,以经过这些点。另一个方法是将图形分段,每段为一个低阶多项式$S(x)$,并在相邻点$(x_k,y_k)$和$(x_{k+1},y_{k+1})$之间进行插值.这样可以保证插值多项式没有高阶多项式插值的摆动性，而且这种插值方法一般是N段的分段函数。这样的分段拟合的函数称之为样条函数。其中一个重要的性质就是插值多项式经过结点。那么，接下来要思考的问题就是每一小段的插值多项式应该选择什么样的多项式。
  首先考虑一阶多项式，即一阶拉格朗日多项式。然而不难想到这种拟合方式在大多数情况下下是不适用的，因为拟合后的曲线为一段一段的折线段，显然不符合拟合的要求。然后再来考虑二阶多项式，二阶多项式能满足平滑的特点，但是会发现其在偶数结点处其曲率变化很大，这很有可能导致有非期望的弯曲或畸变。而且二次样条的导数在其结点处不连续。那么如果使用三次样条，则可以使其一阶二阶导数都连续，然而这个条件仅仅需要其多项式系数满足一定要求即可。不再继续考虑更高阶的样条函数是因为三次样条已经能满足需求，不必要牺牲产生震荡失真的代价去考虑高次样条，而且高次样条的系数增多，使求解变得极其困难。那么三次样条的多项式系数该如何确定呢？
  首先，我们需要给出三次样条需要满足的条件使其是一个光滑连续的函数，即一阶二阶导数在结点处连续。

  其中，性质Ⅰ描述了由分段三次多项式构成的$S(x)$。性质$Ⅱ$描述了对给定数据点集的分段三次插值。性质$Ⅲ$和性质$Ⅳ$保证了分段三次多项式函数是一个光滑连续函数。性质$V$保证了函数的二阶导数也是连续的。
  是否可能构造一个三次样条满足性质$Ⅰ$到性质$V$?每个三次多项式$S(x)$有4个未知常数，因此需要求解$4N$个系数。宽松的讲,要确定$4N$个自由度或条件。数据点提供了$N+1$个条件,性质$Ⅲ$、性质$Ⅳ$和性质$V$都提供了$N-1$个条件,总共确定了$N+1+3(N-1)=4N-2$个条件。这样剩下了两个自由度。.可称之为端点约束( end-point constraints)涉及在点$x0$和$xN$处的导数$S^{\prime }(x)$或$S"(x)$。通过推导，由于二阶导数满足拉格朗日多项式，因此令其满足性质$V$，再通过积分两次，可以求解出$S(x)$的表达式，再利用性质$II$求出积分后不定系数的表达式，因此其表达式为
$$S_k(x)=-\frac{m_k}{6h_k}{\left(x_{k+1}-x\right)}^3+\frac{m_{k+1}}{6h_k}{\left(x-x_k\right)}^3+\left(\frac{y_k}{h_k}-\frac{m_k{h}_k}{6}\right)\left(x_{k+1}-x\right)+\left(\frac{y_{k+1}}{h_k}-\frac{m_{k+1}{h}_k}{6}\right)\left(x-x_k\right)$$   其中系数$h_k$为第$k$个和第$k+1$个结点的差分值，$m_k=S^{\prime \prime }(x_k)$。那么只剩下一阶导数的性质没有用上。通过推到，利用一阶导数的性质，可以确定$m_k$的递推关系式，即
$$h_{k-1}{m}_{k-1}+2\left(h_{k-1}+h_k\right)m_k+h_k{m}_{k+1}=u_k,u_k=6(d_k-d_{k-1}),k=1,2,...,N-1$$  可以发现，可以构造一个有包含$N+1$个未知数具有$N-1$个方程的线性方程组，即端点处的二阶导数值，因此有以下五种策略求解线性方程组。

  因此采用策略可以定出$m_0$的值，则第一个方程可以化简为
$$2\left(h_0+h_1\right)m_1+h_1{m}_2=u_1-h_0{m}_0,whenk=1$$  同理，已知$m_N$的值也可以知道最后一个方程
$$h_{N-2}{m}_{N-2}+2\left(h_{N-2}+h_{N-1}\right)m_{N-1}=u_{N-1}-h_{N-1}{m}_N,whenk=N-1$$  这样，剩下的系数就可以用一个带状的线性方程组来表示，即

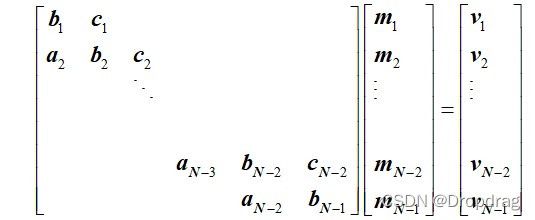
  表示为$HM=V$，利用第三章的几种求解线性方程组的方法，即可确定所有的结点二阶导数值，将这些值带回原插值函数，得到最终的插值函数多项式。到此，三次样条函数插值已经全部构造完成。
  对于五种不同的策略，其求解的 有所不同。具体为：

1. 紧压样条。存在惟一的三次样条曲线,其一阶导数的边界条件是$S^{\prime }(a)=d_0$和$S^{\prime }(b)=d_N$，于是求解的方程组为
   
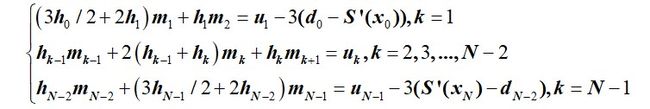
   Mark：紧压样条在端点有斜率。紧压样条可想像为用外力使柔软而有弹性的木杆经过数据点,并在端点处使其具有固定斜率。这样的样条对于画经过多个点的光滑曲线的绘图员相当有用。
2. natural样条。存在惟一的三次样条曲线,其一阶导数的边界条件是 =0和 =0，于是求解的方程组为
   
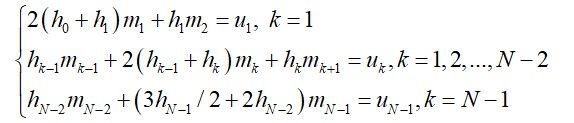
   Mark：natural样条是柔软有弹性的木杆经过所有数据点形成的曲线,但让端点的斜率自由地在某一位置保持平衡,使得曲线的摇摆最小。它在对有多位有效数字精度的试验数据进行曲线拟合时很有用。
3. 外推样条。存在惟一的三次样条曲线,其中通过对点$x_1$和$x_2$进行外推得到 ,同时通过对点$x_{N-1}$和$x_{N-2}$进行外推得到 。于是求解的方程组为
   
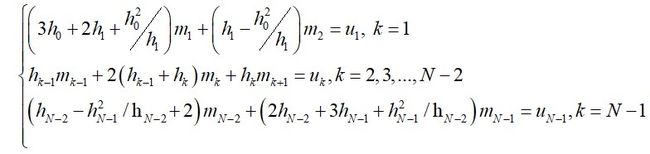
   Mark：外推样条等价于端点处的三次多项式曲线是相邻三次多项式曲线的扩展形成的样条，也就是说,样条曲线在区间$[x_0,x_2]$内形成单个三次多项式曲线,同时在区间$[x_{N-2},x_N]$内形成另一个三次多项式曲线。
4. 抛物线终结样条。存在唯一的三次样条，其中在区间$[x_0,x_1]$内 ,而在$[x_{N-1},x_N]$内， .于是求解的方程组为
   
   Mark：在区间$[x_0,x_1]$内$S"(x)=0$使得在区间$[x_0,x_1]$内三次多项式曲线退化为二次多项式曲线,同时在区间$[x_{N-1},x_N]$内也发生同样的情况。
5. 端点曲率调整样条。存在唯一的三次样条曲线，其中二阶导数的边界条件$S’’(a)$和$S’’(b)$使确定的。于是求解的方程组为
   
   Mark：直接对$S’’(a)$和$S’’(b)$赋值，可调整每个端点的曲率。

  综上所述，无论是哪种策略，其都给出了在端点处的一阶或二阶导数取值以及相应的线性方程组，以此来得出除端点外的所有结点二阶导数值，即$m_k$。然后再通过五种策略的根据其他点二阶导数值来确定端点的二阶导数值，从而确定所有系数，最终求出三次样条插值函数。

4、贝塞尔曲线

  20世纪70年代,雷诺汽车公司的Pierre Bezier和雪铁龙汽车公司的Paul de Castaliau各自独立推导出了CAD/CAM应用中的贝塞尔(Bezier)曲线。这些参数多项式是一类逼近样条。贝塞尔曲线是计算机图形学(CAD/CAM,计算机辅助几何设计)中曲线和曲面表示的基本方法。最初推导的贝塞尔曲线是用递归方法隐式定义的。将它们用伯恩斯坦多项式(Bemnstein polynomial)显式地定义,有助于推导贝塞尔曲线的性质。
  其中，N阶伯恩斯坦多项式的定义为
$$B_{i,N}(t)=\left(\begin{array}{l}N\\ i\end{array}\right)t^i(1-t{)}^{N-i}i=0,1,2,...,N\left(\begin{array}{l}N\\ i\end{array}\right)=\frac{N!}{t!(N-i)!}$$  一般，N阶伯恩斯坦多项式由N+1项。其中，伯恩斯坦多项式具有几个重要的性质。首先，伯恩斯坦多项式具有递归关系，表现为
$$\begin{gathered} B_{0,0}(t)=1,B_{i,N}(t)=0,i<0ori>N \\ {B}_{i,N}(t)=\left(1-t\right)B_{i,N-1}(t)+t{B}_{i-1,N-1}(t)=0,i=1,2,3,...,N-1 \end{gathered}$$  因此，任意一个伯恩斯坦多项式可由其递归关系生成，并为后来的贝塞尔函数求解提供手段。其次，伯恩斯坦多项式还具有非负性，即在区间$[0,1]$上是非负函数。因为伯恩斯坦多项式可以看作n次重复实验的伯努利分布的概率公式，其中t可以视为概率p，即只能在区间$[0,1]$内取值，因此，其值也就是概率一定是处在$[0,1]$内的非负数。第三个性质，伯恩斯坦多项式还具有规范性，即
$$\sum _{i=0}^N{B}_{i,N}(t)=1$$  其规范性可以由二项式定理证明。第四个性质，也就是伯恩斯坦多项式的导数性质，即
$$\frac{d}{dt}{B}_{i,N}(t)=N\left(B_{i-1,N-1}(t)-B_{i,N-1}(t)\right)$$  可以对伯恩斯坦多项式的定义是直接求导，即可证明其导数性质。最后一个性质，也是其可以推导出贝塞尔曲线的最重要的一个性质，就是其可以作为基，即N阶伯恩斯坦多项式组成阶数小于等于N的所有多项式的一个基空间。性质5说明,任何阶数小于等于N的多项式都可以惟一地表示为伯恩斯坦多项式的线性组合。
  给出贝塞尔曲线的定义，给定一个控制点集 ，一条N阶贝塞尔曲线定义为N阶伯恩斯坦多项式的加权和。即N阶贝塞尔曲线可以表示成
$$P(t)=\sum _{i=0}^N{P}_i{B}_{i,N}(t),i=0,1,...,N,t\in [0,1]$$  其中 为N阶伯恩斯坦多项式。控制点是表示平面中x和y坐标的有序对。可将控制点作为向量,而对应的伯恩斯坦多项式作为标量处理,这样公式(28)可参数化表示为$P(t)=(x(t),y(t))$.其中
$$x(t)=\sum _{i=0}^N{x}_i{B}_{i,N}(t),y(t)=\sum _{i=0}^N{y}_i{B}_{i,N}(t),$$  其中$0<t<1$。函数$P(t)$称为向量值函数,或等价地说,函数的值域是$xy$平面上的一个点集。贝塞尔曲线因此也具有一些重要的性质，即$P_0，P_1$在曲线的端点上，即
$$P(0)=\sum _{i=0}^N{P}_i{B}_{i,N}(0)=P_0,P(1)=\sum _{i=0}^N{P}_i{B}_{i,N}(1)=P_N$$  而其他点却不一定在曲线上，事实上大多数的点都不在曲线上。其次，贝塞尔曲线在$[0,1]$上具有连续性，且具有任意阶导数。因此推导后有
$$\begin{gathered} P^{\prime }(0)=\sum _{i=0}^N{P}_{i}N\left(B_{i-1,N-1}(0)-B_{i,N-1}(0)\right)=N(P_1-P_0) \\ {P}^{\prime }(1)=N(P_N-P_{N-1}) \end{gathered}$$  最后一个性质基于凸集的概念。即凸集的定义为，如果$xy$平面上的子集C中任意两点连线上的所有点都是集合C中的元素,则称C为凸集。并且有如下定义，集合C的凸包是包含C的所有凸集的交。点的一个凸组合必定是该点集的凸包的子集。由伯恩斯坦多项式性质知,贝塞尔曲线是控制点的凸组合,因此它必定落在控制点的凸包内部。即有性质4贝塞尔曲线落在它的控制点集的凸包内。该性质说明,N阶贝塞尔曲线是一条连续曲线,并为其控制点集 的凸包所限,该曲线分别在点$P_0$和$P_1$处开始和结束。贝塞尔观察到,曲线依次被"拉向"其余的合个不同。
  贝塞尔曲线的有效性在于,通过对控制点进行微小的调整,可以方便地调整(通过鼠标、键盘或其他图形界面)曲线的形状。改变任意一个控制点的坐标,将使整条曲线在参数区间$0\le t\le 1$的形状发生变化。然而这一变化在一定程度上是局部的,因为对应于控制点P的伯恩斯坦多项式在参数值$t=k/N$处有最大值。因此,该贝塞尔曲线形状的最大变化应该在点$P(k/N)$附近。这样,创建一条特定形状的曲线只需对初始控制点集做相对较少的改变。这样一条重要的特性在计算机辅助设计绘图中具有重要的作用，相较于样条插值，其没有高阶项，因其具有规范性，因此在变换时其可以有效地避免失真。

5、三角多项式原理

   通常在工业生产中，会遇到一些具有周期性的信号。那么对于一些具有周期性的函数，怎样的拟合方式能够使得拟合更加完善呢？经过思考发现，一个具有周期性的函数，能够表示为由$a_{j}cos(jx)$和$b_{j}sin(jx)$线性组合的多项式表示。因此下面给出如下定义：如果存在值$t_0,t_1,\dots ,t_x$满足$a=t_0<t_1<\dots <t_x=b$,函数$f(x)$在每个开区间$t_{i-1}<x<t_i,i=1,2,\dots ,K$内是连续的,而且函数在每个端点$t_i$有左极限和右极限,则称函数$f(x)$在区间$[a,b]$内分段连续。那么对于在一定区间内是分段连续且具有周期性的函数，可以将其展开为傅里叶级数的形式。设$f(x)$是周期函数,周期为$2\Pi$而且$f(x)$在区间$[-\Pi ,\Pi ]$内分段连续,则$f(x)$的傅里叶级数$S(x)$表示为
$$S(x)=\frac{a_0}{2}+\sum _{j=1}^{\infty }(a_j\cos (jx)+b_j\sin (jx))$$   其中系数可以由欧拉公式得到，也可由三角函数系的正交性及其模得出，因此其中系数表达式为

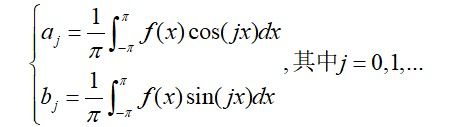
   其中，设$S(x)$是$f(x)$在区间$[-\Pi ,\Pi ]$内的傅里叶级数。如果$f(x)$在区间$[-\Pi ,\Pi ]$内是分段连续的,而且在区间内的每个端点有左导数和右导数,则$S(x)$对于所有$x\in [-\Pi ,\Pi ]$是收敛的。对于所有的点$x\in [-\Pi ,\Pi ]$，存在关系式$S(x)=f(x)$其中$f(x)$是连续的。如果$x=a$是函数f的不连续点,则 ,这里分别表示左极限和右极限。这样,可得到傅里叶级数扩展表达式:
$$f(x)=\frac{a_0}{2}+\sum _{j=1}^{\infty }(a_j\cos (jx)+b_j\sin (jx))$$   如果函数$f(x)$为奇函数或者偶函数的时候，则由系数的确定公式可以知道，其中$a_j$或$b_j$会等于0，也就是说，$f(x)$的傅里叶级数仅含正弦函数或者余弦函数，通过公式可以确定此时的系数。最后，我们称形如
$$T_M(x)=\frac{a_0}{2}+\sum _{j=1}^M(a_j\cos (jx)+b_j\sin (jx))$$   含有正余弦函数的多项式为三角多项式。因此，可以看见，三角多项式是傅里叶级数的近似解形式，当阶数越高时其误差越小，因此可以用来拟合函数。因为在实际工程中，当知道一个函数的某些点取值时，可以利用离散傅里叶级数进行三角多项式逼近，可以证明，三角多项式是使其均方误差最小的多项式。经过推导可知，其三角多项式的系数为;
$$\begin{gathered} a_j=\frac{2}{N}\sum _{k=1}^{N}f(x_k)\cos (j{x}_k),j=0,1,...,M \\ {b}_j=\frac{2}{N}\sum _{k=1}^{N}f(x_k)\sin (j{x}_k),j=1,2,...,M \end{gathered}$$
   其中，需已知函数的$N+1$个点，并且横坐标之间等距且$x\in [-\Pi ,\Pi ]$，则可展开为M阶三角多项式。尽管用最小二乘法定义,但可看成是连续傅里叶级数的数值近似值。欧拉公式给出了连续函数的傅里叶级数的系数,而给出了对数据点集进行曲线拟合的三角多项式系数。当使用更多的数据点时,三角多项式的系数更接近傅里叶级数的系数。

二、实验内容及核心算法代码

1、最小二乘拟合曲线原理实现

  由第一节原理部分可知，设$\{(x_k,y_k){\}}_{k=1}^N$是一个N个点的集合，其中横坐标是确定的。那么，理想的最小二乘拟合曲线$y=f(x)=Ax+B$的拟合结果应满足是均方根误差最小的曲线。那么，所选定的$A，B$构成的拟合曲线应当使$E_2(f)$的值当且仅当所选取的$A，B$值处最小。也就是说，数据点到曲线的垂直距离平方和最小，其最小值为 。其系数$A，B$满足所示的正规方程。因此，仅需要知道点集合就可求出其拟合曲线的相关系数。
其大致过程为：

1. 获取所要拟合的点集合，并写出误差平方和表达式
2. 对每个待定参数求偏导，并列出正规方程
3. 求解线性方程组，得到最小二乘拟合曲线系数

  以下通过实例来进行最小线性二乘拟合的实验。
（a） 根据数据$\{(x_k,y_k){\}}_{k=1}^{50}$，其中$x_k=(0.1)k且y_k=x_k+cos(k_{1/2})$，求解 最小二乘线性拟合。
（b） 计算$E_2(f)$.
（c） 在同一坐标系下，画出点集和最小二乘线性拟合曲线。
  由题意可知，根据给出的$x，y$之间的关系可以生成由50个点所组成的集合。因此当进行最小线性二乘拟合的时候，可以列出其正规方程，并计算求解即得出其拟合曲线。然后，根据求出的拟合曲线，即可以计算其均方根误差，并绘制其曲线。
其核心函数算法代码为：

//the xpt,ypt are the point set coordinate,and the A,B are the coefficient of the curve
//n is the size of the point set
void CmpcurvebyLeastSquare(float* xpt, float* ypt, float& A, float& B, const int n, float** val = NULL)
{
	float xk2, xk, xkyk, yk;
	float sumxk2, sumxk, sumxkyk, sumyk;
	sumxk2 = 0, sumxk = 0, sumxkyk = 0, sumyk = 0;
	//if user give the val argument,note down the step-value
	for (int i = 0; i < n && val != NULL; ++i)
	{
		xk = xpt[i];
		yk = ypt[i];
		xk2 = xk * xk;
		xkyk = xk * yk;
		val[i][0] = xk;
		val[i][1] = yk;
		val[i][2] = xk2;
		val[i][3] = xkyk;
		sumxk += xk;
		sumyk += yk;
		sumxk2 += xk2;
		sumxkyk += xkyk;
	}
	if (val != NULL)
	{
		val[n][0] = sumxk;
		val[n][1] = sumyk;
		val[n][2] = sumxk2;
		val[n][3] = sumxkyk;
	}
	float** mat;
	float* vB, * X;
	mat = MallocArr(2, 2);
	vB = MallocArr(2);
	X = MallocArr(2);
	mat[0][0] = sumxk2; mat[0][1] = sumxk; mat[1][0] = sumxk; mat[1][1] = n;
	vB[0] = sumxkyk; vB[1] = sumyk;
	//as solve the AB linear system,use gauss elem to solve out the AB
	GaussElimmethodtoLinearsystem(mat, vB, X, 2);
	A = X[0]; B = X[1];
	FreeArr(mat, 2); FreeArr(vB); FreeArr(X);
}

2、曲线拟合原理实现

  由第一节原理部分可知，对于不是线性关系的曲线拟合，可以对其进行线性化操作再利用最小二乘法求出其系数的表达式即可。也就是说，对于一组不具有线性关系的数据点集合，可以对其进行诸如取对数、指数的方法将其变换为具有线性关系的表达式，即将数据点$xk,yk$变换成$XY$平面上具有线性关系的点集$Xk,Yk$,再利用最小二乘法求出变换后的曲线表达式，最后再变换为原变量的表达式。
因此，无论对于具有什么样关系的数据点集合，只要能够大致确定其函数类型，就可以通过相应的变换与换元进行最小二乘线性拟合，从而刻画出其函数关系。
其大致过程如下;

1. 确定数据点集合的函数关系，写出其通解与待定系数。
2. 将通解进行如取指对数、三角换元等方法转化成具有线性关系的变量，并求解新变量的最小二乘拟合曲线的系数与表达式。
3. 将求出系数的表达式变换回原变量的关系式，得到最终曲线拟合的表达式。

以下通过实例来进行曲线拟合的实验。
洛杉矶郊区在11月8日的温度记录如下表所示。共有24个数据点。
（a） 使用fmins命令，对给定的数据集求解最小二乘曲线$f(x)=Acos(Bx)+Csin(Dx)+E$。
（b） 求$E_2(f)$。
（c） 在同一坐标系下绘制点集和（a）得出的最小二乘曲线。

时间,p.m.	温度	时间,a.m.	温度
1	66	1	58
2	66	2	58
3	65	3	58
4	64	4	58
5	63	5	57
6	63	6	57
7	62	7	57
8	61	8	58
9	60	9	60
10	60	10	64
11	59	11	67
午夜	58	正午	68

由题意可知，使用matlab中的fminsearch命令求解最小化$E(A，B，C，D，E)$后的A和C的近似值。首先在matlab中定义$E(A,B,C,D,E)$为一个M文件，在另外一个源文件中使用fminsearch命令和初始值全设置为1.0，可以得到非线性最小二乘拟合的表达式的系数。
  其核心函数算法代码为：

function z=E(u)
A=u(1);
B=u(2);
C=u(3);
D=u(4);
E=u(5);
z=(A.*cos(B.*1)+C.*sin(D.*1)+E-58).^2+(A.*cos(B.*2)+C.*sin(D.*2)+E-58).^2+...
(A.*cos(B.*3)+C.*sin(D.*3)+E-58).^2+(A.*cos(B.*4)+C.*sin(D.*4)+E-58).^2+... (A.*cos(B.*5)+C.*sin(D.*5)+E-57).^2+(A.*cos(B.*6)+C.*sin(D.*6)+E-57).^2+... (A.*cos(B.*7)+C.*sin(D.*7)+E-57).^2+(A.*cos(B.*8)+C.*sin(D.*8)+E-58).^2+... (A.*cos(B.*9)+C.*sin(D.*9)+E-60).^2+(A.*cos(B.*10)+C.*sin(D.*10)+E-64).^2+... (A.*cos(B.*11)+C.*sin(D.*11)+E-67).^2+(A.*cos(B.*12)+C.*sin(D.*12)+E-68).^2+... (A.*cos(B.*13)+C.*sin(D.*13)+E-66).^2+(A.*cos(B.*14)+C.*sin(D.*14)+E-66).^2+... (A.*cos(B.*15)+C.*sin(D.*15)+E-65).^2+(A.*cos(B.*16)+C.*sin(D.*16)+E-64).^2+... (A.*cos(B.*17)+C.*sin(D.*17)+E-63).^2+(A.*cos(B.*18)+C.*sin(D.*18)+E-63).^2+... (A.*cos(B.*19)+C.*sin(D.*19)+E-62).^2+(A.*cos(B.*20)+C.*sin(D.*20)+E-61).^2+... (A.*cos(B.*21)+C.*sin(D.*21)+E-60).^2+(A.*cos(B.*22)+C.*sin(D.*22)+E-60).^2+... (A.*cos(B.*23)+C.*sin(D.*23)+E-59).^2+(A.*cos(B.*24)+C.*sin(D.*24)+E-58).^2;

3、样条函数插值原理实现

  有第一节原理部分可知，将图形分段,每段为一个低阶多项式$S(x)$,并在相邻点$(x_k,y_k)$和$(x_{k+1},y_{k+1})$之间进行插值.这样可以保证插值多项式没有高阶多项式插值的摆动性，而且这种插值方法一般是N段的分段函数。这样的分段拟合的函数称之为样条函数。使用三次样条，则可以使其一阶二阶导数都连续，然而这个条件仅仅需要其多项式系数满足一定要求即可。不再继续考虑更高阶的样条函数是因为三次样条已经能满足需求，不必要牺牲产生震荡失真的代价去考虑高次样条，而且高次样条的系数增多，使求解变得极其困难。
  因此，求解一个三次样条插值函数最重要的点就在于如何选取策略以及求解端点二阶导数值，其中求解除端点处二阶导数值的步骤大同小异，因此不需要放在重点考虑。
  因此，下面通过一个实例来展现natural样条的逼近效果。

• 下面的表给出了在洛杉矶的郊区12小时内每个小时的温度(华氏温度)。根据这些数据求natural三次样条插值。在同–坐标系中,画出natural三次样条插值和这些数据。根据natural三次样条插值和习题12的(a)部分的结论求12小时内的平均温度近似值

时间,a.m.	温度	时间,a.m.	温度
1	58	7	57
2	58	8	58
3	58	9	60
4	58	10	64
5	57	11	67
6	57	12	68

  根据前述步骤，其基本流程为：

1. 根据数据算出已知的基本的参数，包括$h_k,d_k,u_k$等。
2. 根据所选择的策略列出线性方程组，并求解除端点外的二阶导数值。
3. 根据求出的系数以及选定的策略，求解端点处的二阶导数值。
4. 将系数带回原多项式，得到最终的三次样条插值多项式。

  其核心函数算法代码为：

//cmp the hk coe,so must pass the point info,and save the data in the Hk,so have N+1-points,N-Hk;k=0,1,2...N-1
//the formula is hk = x(k+1) - x(k),the N>=1
void CmpHkcoeofSplFunc(float* xpt, const int N, float* Hk)
{
	if (N < 1)
	{
		cout << "arguments error!" << endl;
		return;
	}
	for (int i = 0; i < N; ++i)
	{
		Hk[i] = xpt[i + 1] - xpt[i];
	}
}
//cmp the dk coe,so must pass the point info,and save the data in the Hk,so have N+1-points,N-Dk;k=0,1,2..N-1 
//the formula is dk = ( y(k+1)-y(k) ) / hk
void CmpDkcoeofSplFunc(float* xpt, float* ypt, const int N, float* Dk)
{
	float* Hk;
	float dy;
	Hk = MallocArr(N);
	CmpHkcoeofSplFunc(xpt, N, Hk);
	for (int i = 0; i < N; ++i)
	{
		dy = ypt[i + 1] - ypt[i];
		Dk[i] = dy / Hk[i];
	}
	FreeArr(Hk);
}
//cmp the uk coe,so must pass the point info,and save the data in the Hk,so have N+1-points,N-1-Uk;k=1,2,3...N-1
// so the Uk only exist in the knot except the endpoints
//the formula is uk = 6 * ( d(k) - d(k-1) )
void CmpUkcoeofSplFunc(float* xpt, float* ypt, const int N, float* Uk)
{
	float* Dk;
	Dk = MallocArr(N);
	CmpDkcoeofSplFunc(xpt, ypt, N, Dk);
	for (int i = 1; i < N; ++i)
	{
		Uk[i-1] = 6 * (Dk[i] - Dk[i - 1]);
	}
	FreeArr(Dk);
}
//as have the Mk,so cmp the Ski,which have N Hk,Dk,Ski,N+1 Mk
void CmpSkiwithMk(float *ypt, float* Mk, float* Hk, float* Dk, float** Ski, const int N)
{
	float val1, val2;
	for (int i = 0; i < N; ++i)
	{
		val1 = 2 * Mk[i] + Mk[i + 1];
		val2 = Mk[i + 1] - Mk[i];
		Ski[i][0] = ypt[i];
		Ski[i][1] = Dk[i] - Hk[i] * val1 / 6;
		Ski[i][2] = Mk[i] / 2;
		Ski[i][3] = val2 / (6 * Hk[i]);
	}
}
//Spline function(样条函数)
//the natural spline function
//pass the poitn coordinate as the arguments and the num of the spline function,equally how many points
//save the coefficient in the Sk,so solve out the polynomial
//the point coordinate xpt,ypt,and have N+1 point and Ski,so have N spline function
//so should cmp the N<1,
void CmpNaturalSplFunSki(float* xpt, float* ypt, const int N, float** Ski)
{
	//if N<=1,the spline function is 1-order Lagrange polynimial or does not exist
	if (N <= 1)
	{
		cout << "the num of spline function is an error!" << endl;
		return;
	}
	//construct the Mk
	float* Mk, * Hk, * Uk, * Dk;
	Mk = MallocArr(N + 1);
	Hk = MallocArr(N);
	Uk = MallocArr(N - 1);
	Dk = MallocArr(N);
	CmpHkcoeofSplFunc(xpt, N, Hk);
	CmpUkcoeofSplFunc(xpt, ypt, N, Uk);
	CmpDkcoeofSplFunc(xpt, ypt, N, Dk);
	//the N=2
	if (N == 2)
	{
		Mk[0] = 0; Mk[N] = 0;
		Mk[1] = Uk[0] / (2 * (Hk[0] - Hk[1]));
		CmpSkiwithMk(ypt, Mk, Hk, Dk, Ski, N);
		return;
	}
	//the N=3
	if (N == 3)
	{
		Mk[0] = 0; Mk[N] = 0;
		float** H;
		H = MallocArr(N - 1, N - 1);
		H[0][0] = 2 * (Hk[0] + Hk[1]); H[0][1] = Hk[1];
		H[1][0] = Hk[1]; H[1][1] = 2 * (Hk[1] + Hk[2]);
		float* M;
		M = MallocArr(N - 1);
		GaussElimmethodtoLinearsystem(H, Uk, M, N - 1);
		Mk[1] = M[0]; Mk[2] = M[1];
		CmpSkiwithMk(ypt, Mk, Hk, Dk, Ski, N);
		PrintMatrix(Ski,N,4);
		return;
	}
	//the N>=4,so have M matrix
	//construct the H matrix
	float** H;
	H = MallocArr(N - 1, N - 1);
	H[0][0] = 2 * (Hk[0] - Hk[1]); H[0][1] = Hk[1];
	H[N - 2][N - 3] = Hk[N - 2]; H[N - 2][N - 2] = 2 * (Hk[N - 2] + Hk[N - 1]);
	for (int i = 1; i < N - 2; ++i)
	{
		H[i][i - 1] = Hk[i];
		H[i][i] = 2 * (Hk[i] + Hk[i + 1]);
		H[i][i + 1] = Hk[i + 1];
	}
	//solve Hk with the strategy natural spline function
	Mk[0] = 0; Mk[N] = 0;
	float* M;
	M = MallocArr(N - 1);
	GaussElimmethodtoLinearsystem(H, Uk, M, N - 1);
	for (int i = 1; i <= N - 1; ++i)
	{
		Mk[i] = M[i - 1];
	}
	//solve the Ski coefficient
	CmpSkiwithMk(ypt, Mk, Hk, Dk, Ski, N);
	//free
	FreeArr(Hk);
	FreeArr(Dk);
	FreeArr(Uk);
	FreeArr(Mk);
	FreeArr(H, N - 1);
	FreeArr(M);
}

4、三角多项式原理实现

  由第一节原理部分可知，一个具有周期性的函数，能够表示为由$a_{j}cos(jx)$和$b_{j}sin(jx)$线性组合的多项式表示。因此下面给出如下定义：如果存在值$t_0,t_1,\dots ,t_x$满足$a=t_0<t_1<\dots <t_x=b$,函数$f(x)$在每个开区间$t_{i-1}<x<t_i,i=1,2,\dots ,K$内是连续的,而且函数在每个端点ti有左极限和右极限,则称函数$f(x)$在区间$[a,b]$内分段连续。那么对于在一定区间内是分段连续且具有周期性的函数，可以将其展开为傅里叶级数的形式。
  因此，对于一个具有周期性的函数，只需要对其一段周期上进行离散傅里叶级数展开，即可得到其三角多项式的逼近公式。在利用其周期性，即可求出其他区间上的点的值。
  通过以下实例可以展现如何求解并利用三角多项式拟合函数。
  与前述实例相同。
洛杉矶郊区在11月8日的温度记录如下表所示。共有24个数据点。
（a）求三角多项式$T_7(x)$.
（b）在同一坐标系下绘制点集和（a）得出的三角多项式曲线。

时间,p.m.	温度	时间,a.m.	温度
1	66	1	58
2	66	2	58
3	65	3	58
4	64	4	58
5	63	5	57
6	63	6	57
7	62	7	57
8	61	8	58
9	60	9	60
10	60	10	64
11	59	11	67
午夜	58	正午	68

  根据已知条件可知，已知时间为1-24的各个温度值，当利用三角多项式进行拟合时，首先需要将其横坐标转换为$[-\Pi ,\Pi ]$上的等距节点，才能求解出其三角多项式，因此与最小二乘拟合不同，需要一个提前对横坐标进行预处理。
利用已知点求解三角多项式的基本步骤为：

1. 得到N+1个已知节点，并对其进行坐标变换 ，使其横坐标为位于区间$[-\Pi ,\Pi ]$等距已知节点。
2. 利用系数公式，根据所需要求解多项式的阶数，求解其三角多项式。

  其核心函数算法代码为

//the xk,yk is the data point set,the size of it is N,and the M is the order-number of the trigonometric polynomial
//store the result in the aj,bj
void CmpTrigopolyCoe(float* xk, float* yk, const int N, const int M, float* aj, float* bj)
{
	//cmp the aj,bj
	aj[0] = 0;
	for (int i = 0; i < N; ++i)
	{
		aj[0] += yk[i];
	}
	//cmp the first ele
	aj[0] = 2 * aj[0] / float(N);
	bj[0] = NULL;
	for (int i = 1; i <= M; ++i)
	{
		float sumcos = 0, sumsin = 0;
		//cmp the least-square coe
		for (int j = 0; j < N; ++j)
		{
			sumcos += yk[j] * cos(i * xk[j]);
			sumsin += yk[j] * sin(i * xk[j]);
		}
		//cmp the i-th aj,bj
		aj[i] = 2 * sumcos / float(N);
		bj[i] = 2 * sumsin / float(N);
	}
}
//cmp the value of the trigonometric polynomial,the n is the order of the poly
float CmpTrigonoPolyValue(float* aj, float* bj, const int n, float x)
{
	float y = aj[0] / 2;
	float cosv, sinv;
	for (int i = 1; i <= n; ++i)
	{
		cosv = aj[i] * cos(i * x);
		sinv = bj[i] * sin(i * x);
		y += (cosv + sinv);
	}
	return y;
}

5、贝塞尔曲线原理实现

  由第一节原理部分可知，贝塞尔曲线是计算机图形学(CAD/CAM,计算机辅助几何设计)中曲线和曲面表示的基本方法。推导的贝塞尔曲线是用递归方法隐式定义的。贝塞尔曲线是控制点的凸组合,因此它必定落在控制点的凸包内部。贝塞尔曲线的有效性在于,通过对控制点进行微小的调整,可以方便地调整(通过鼠标、键盘或其他图形界面)曲线的形状。改变任意一个控制点的坐标,将使整条曲线在参数区间$0\le t\le 1$的形状发生变化。
  因此，可以通过设计控制点的位置来设计贝塞尔曲线的样式，以此设计出更加复杂与大小位置可控的图形。由于贝塞尔曲线的定义及其性质使得其具有非常良好的不失真的特性，即其始终位于凸包范围内，从而便于计算机的几何设计。
  因此，通过以下实例来绘制并体会贝塞尔曲线的特性。

• 编写程序,生成并绘制组合贝塞尔曲线。利用该程序生成和绘制过3个控制点集{(0,0),(1,2),(1,1),(3,0)},{(3,0),(4,-1),(5,-2),(6,1),(7,0)}和{(7,0),(4,- 3),(2,- 1),(0,0)}的贝塞尔曲线。

  由贝塞尔曲线的显式定义可知，既然给出了贝塞尔曲线的控制点集，就可以确定其阶数N。然后，利用伯恩斯坦多项式的递归的特性可以求出$t$在$[0,1]$范围内的函数表达式，将控制点集作为向量处理，由此可以得到不同t对应的点的向量，从而求出其贝塞尔曲线的$x，y$方向上的分量，从而绘制出控制点集下的N阶贝塞尔曲线。
  其基本流程为：

1. 根据控制点集确定贝塞尔曲线的阶数N。
2. 利用伯恩斯坦多项式的递归特性，将控制点集作为向量处理，伯恩斯坦多项式作为标量处理，求出其在$x，y$上的分量的表达式。
3. 对$t$在$[0,1]$范围内绘制贝塞尔曲线。

  其核心函数算法代码为：

//recursion to cmp the value of the Bernstein polynomial value
//the polynomial is B(i,N)(t)
float BernsteinPolyValue(const int i, const int N, float t)
{
	if (i == 0)
	{
		return powf(1 - t, float(N));
	}
	if (i == N)
	{
		return powf(t, float(N));
	}
	return (1 - t) * BernsteinPolyValue(i, N - 1, t) + t * BernsteinPolyValue(i - 1, N - 1, t);
}
//cmp the Bezier curve value in each point given by tk
//it's N-order Bezier curve,so have N+1 set of control points,and samply n point t in [0,1]
//xk and yk are the set of control points,Xt and Yt are the value of each tk
void CmpBezierCurveValueVec(float* xk, float* yk, float* t, float* Xt, float* Yt, const int N, const int n)
{
	float xval, yval, tk, Berval;
	for (int i = 0; i < n; ++i)
	{
		xval = 0, yval = 0;
		tk = t[i];
		for (int j = 0; j <= N; ++j)
		{
			Berval = BernsteinPolyValue(j, N, tk);
			xval += xk[j] * Berval;
			yval += yk[j] * Berval;
		}
		Xt[i] = xval;
		Yt[i] = yval;
	}
}

---

三、结果分析

1、最小二乘拟合曲线实例分析

  由实验数据结果可以看出，其线性拟合效果是非常好的，其中题目中所给的$x，y$关系式中含有余弦项，即可视为$x，y$线性关系的波动，因此进行线性拟合的时候其理性误差应当控制在1以内，而结果可以看出，其效果相当好。通过图2可以直观地看出其拟合效果是特别好的，因此最小二乘线性拟合法对于具有线性关系的数据具有良好的拟合效果。

2、曲线拟合实例分析

  由图（3）可以直观看出，对于没有规律的数据点集合，进行非线性最小二乘曲线拟合后的结果的曲线走向大致与数据点相同，因此可以判定其拟合效果优良。除此之外，还可以发现数据点均匀的落在拟合曲线两侧，说明拟合曲线可以很好的刻画其变化规律且其数值对于原数据没有较大偏差，因此具有一定的参考价值。通过表（3）也可以看出，拟合曲线的误差在0附近摆动，且相对误差较小，可以更加确定判定拟合曲线对数据具有良好的拟合效果。综上所述，通过finsearch命令求解的拟合曲线具有良好的拟合特性。

3、样条函数插值实例分析

  由表（4）可以看出三次样条插值拟合的取值情况，而从图（3）可以直接看出，利用三次样条的natural样条策略能够使得曲线拟合变得平滑，并且可以直观看出，在结点处满足样条插值的性质I和性质II，因此，三次样条具有良好的插值特性，可以推测使用其他样条策略同样能够具有如此的精度，并且相较于拉格朗日多项式插值而言，其拟合特性以及平滑度提高了很多，是一种非常不错的拟合方法。

4、三角多项式实例分析

  由表（4）可以看出，在求解出来的三角多项式中，变换后的坐标对应的函数值如表所示，通过绘制曲线可以直观看出，将原数据点也进行坐标变换，使其位于区间[-Π，Π]上，可以看出，拟合曲线在端点处出现较大偏差，而在中间区域具有较好的拟合效果。其原因为由于三角多项式的特点，在端点处会有较大波动，因为三角函数的极大值与零点出现在端点处，因此会出现端点拟合失真的情况，但是从中间部分数据可以看出，其拟合效果以及曲线走势与原数据点相同，因此三角多项式具有良好的拟合特性，可以推测当多项式的阶数增加时，其拟合效果会更加良好。

5、贝塞尔曲线实例分析

  由表（5）可以看出在不同控制点集下贝塞尔曲线的取值情况，可以看出，在每个控制点集的端点处，都位于贝塞尔曲线上，因此可以验证贝塞尔曲线的一条性质。由图（4）可以看出贝塞尔曲线的形状。可以看出，在控制点集发生明显突变的情况下，贝塞尔曲线并没有出现明显失真，曲线走向与控制点集的走向相同，且在各个分段的凸包内，因此贝塞尔曲线具有良好的图形表示性质。

---

四、结论

  综上所述，通过分析各个曲线拟合方法的原理，可以发现各个拟合方法的优点。其中，线性或曲线最小二乘拟合方法适用于寻找数据点的规律，即通过最小二乘法来求取推测函数模型的系数，但是并不要求其拟合曲线一定要过各个数据点，因此适合于寻找一般数学物理规律的情况下。其次，样条插值拟合以及三角多项式拟合适用于希望无限逼近于数据点的情况下，即刻画数据点的曲线模型，直观的看出数据点的数学规律，并且三次样条插值具有非常好的曲线特征。最后，贝塞尔曲线适用于设计曲线形状，通过给定控制点集来求解位于凸包内的不失真的函数图像，以此来通过计算机辅助作图。因此，可以通过判定不同的场景，来选取最适当的曲线拟合方式。

---

声明：本系列《数值计算方法》所有章节源代码均为作者编写，大家可以自行下载，仅供学习交流使用，欢迎大家评论留言或者私信交流，请勿用于任何商业行为。其中，各章实验数据结果也在资源链接中，大家可以自行实验对照，欢迎大家批评指正！文件中每个算法均由作者进行初步测试，部分算法可直接用于工程开发作为模块参考。

各章算法源代码（C++）