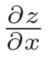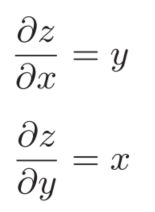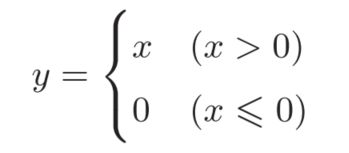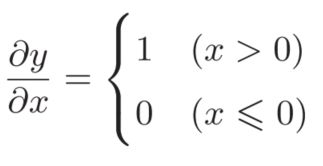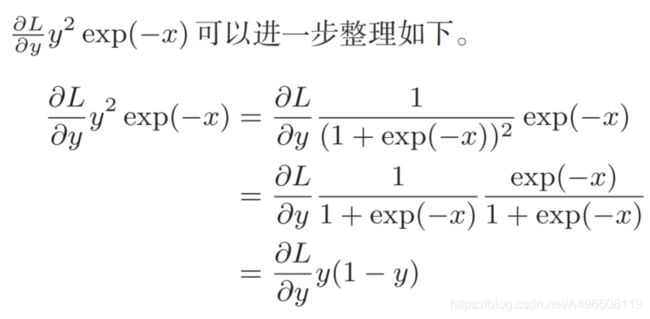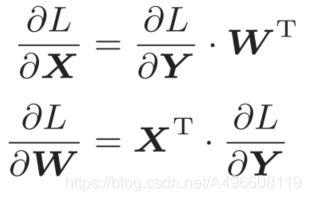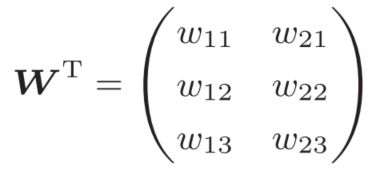通俗易懂的反向传播法（python 代码实现）

目录

 

1. 计算图

1.1 计算图的优点

2. 链式法则

2.1 计算图的反向传播

2.2 什么是链式法则

2.3 链式法则和计算图

2.3 反向传播

2.3.1 加法节点的反向传播

2.3.2 乘法节点的反向传播

2.2.4 苹果例子

3.简单层的实现

3.1 乘法层的实现

3.2 加法层的实现

4 激活函数层的实现

4.1 ReLU层

4.2 Sigmoid层

5 Affine/Softmax层的实现

5.1 Affine层

5.2 批版本的Affine

5.3 Softmax-with-Loss层

6 误差反向传播的实现

---

1. 计算图

计算图将计算过程用图形表示出来。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。
用计算图求解几个常见的问题：

问题1： 太郎在超市买了2个100日元一个的苹果，消费税是10%，请计算支付金额。

问题2： 太郎在超市买了2个苹果、 3个橘子。其中，苹果每个100日元，橘子每个150日元。消费税是10%，请计算支付金额。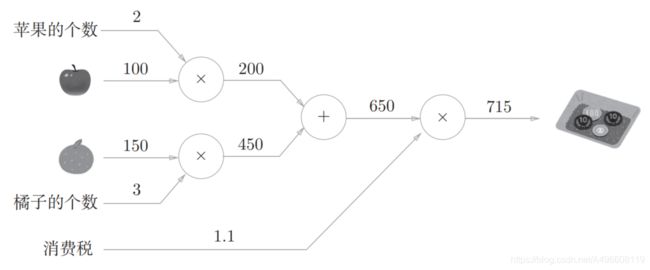

综上，用计算图解题的情况下，需要按如下流程进行。
1.构建计算图。
2.在计算图上，从左向右进行计算。
这里的第2歩“从左向右进行计算”是一种正方向上的传播，简称为正向传播（forward propagation）。正向传播是从计算图出发点到结束点的传播。既然有正向传播这个名称，当然也可以考虑反向（从图上看的话，就是从右向左）的传播。实际上，这种传播称为反向传播（backward propagation）。反向传播将在接下来的导数计算中发挥重要作用。

1.1 计算图的优点

优点1：局部计算使各个节点致力于简单的计算，从而简化问题，如下图所示

优点2：利用计算图可以将中间的计算结果全部保存起来（比如，计算进行到2个苹果时的金额是200日元、加上消费税之前的金额650日元等）。

优点3：可以通过反向传播高效计算导数

2. 链式法则

反向传播将局部导数向正方向的反方向（从右到左）传递，传递这个局部导数的原理，是基于链式法则（chain rule）

2.1 计算图的反向传播

假设存在y = f(x)的计算，这个计算的反向传播如下图所示：

反向传播的计算顺序是，将信号E乘以节点的局部导数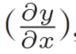，然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中y = f(x)的导数，也就是y关于x的导数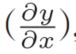。比如，假设y = f(x) = x^2，
则局部导数为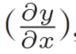 = 2x。把这个局部导数乘以上游传过来的值（本例中为E），然后传递给前面的节点。

2.2 什么是链式法则

深度学习-链式求导：https://blog.csdn.net/weixin_40476348/article/details/94434483 （这位博主介绍的很详细）

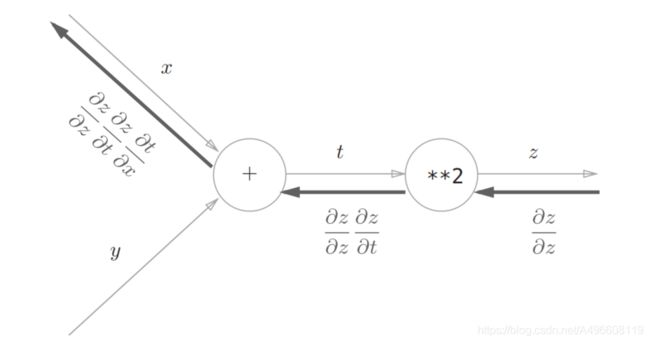
2.3 链式法则和计算图

“**2”节点表示平方运算
根据链式法则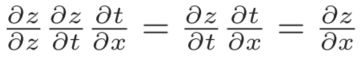，成立，对应“z关于x的导数”。也就是说，反向传播是基于链式法则的。

的结果为2(x + y)

 

2.3 反向传播

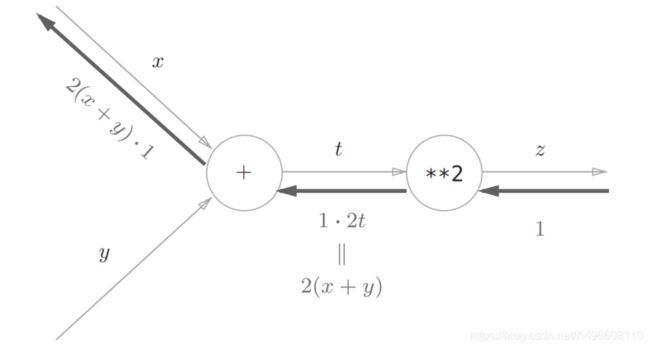
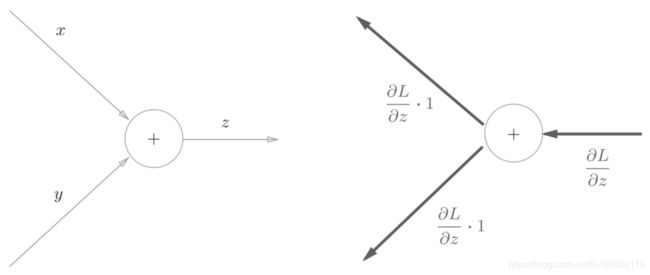
2.3.1 加法节点的反向传播

首先来考虑加法节点的反向传播。这里以z = x + y为对象，观察它的反向传播。 z = x + y的导数可由下式（解析性地）计算出来。

由图可知加法节点的反向传播只是将输入信号输出到下一个节点
 

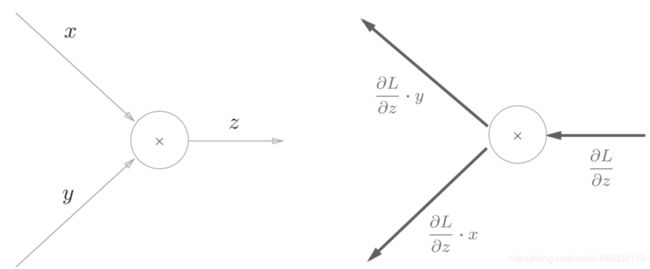
2.3.2 乘法节点的反向传播

我们考虑z = xy，这个式子的导数用下式表示。

由图乘法的反向传播需要正向传播时的输入信号值，案列如下图所示：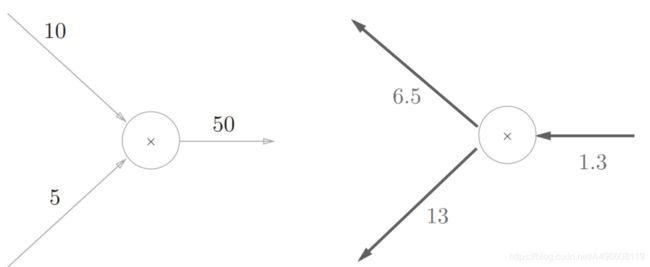

因为乘法的反向传播会乘以输入信号的翻转值，所以各自可按1.3 × 5 =6.5、 1.3 × 10 = 13计算。
 

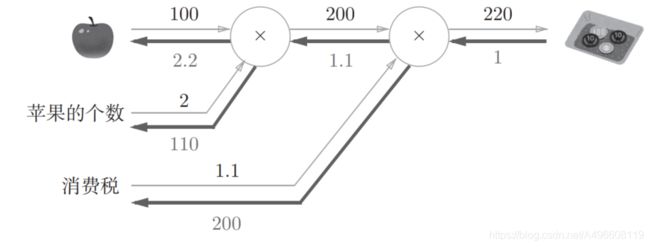
2.2.4 苹果例子

3.简单层的实现

3.1 乘法层的实现

 

层的实现中有两个共通的方法（接口） forward()和backward()。 forward()对应正向传播， backward()对应反向传播。
 

class MulLayer:
    def __init__(self):  # 初始化x,y
        self.x = None
        self.y = None

    def forward(self, x, y): # 接受x和y两个参数，将他们相乘后输出
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):  # 将从上游传来的导数（dout）乘以正向传播的翻转值，然后传给下游
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy

# coding: utf-8


class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy



apple = 100
apple_num = 2
tax = 1.1

mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dTax:", dtax)

3.2 加法层的实现

class AddLayer:
    def __init__(self): # 不需要进行初始化
        pass

    def forward(self, x, y): #  接受x和y两个参数，将它们相加后输出
        out = x + y

        return out

    def backward(self, dout): # 将上游传来的导数（dot）原封不动地传递给下游
        dx = dout * 1
        dy = dout * 1

        return dx, dy

# coding: utf-8


class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy


class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy


apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3)
price = mul_tax_layer.forward(all_price, tax)  # (4)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dOrange:", dorange)
print("dOrange_num:", int(dorange_num))
print("dTax:", dtax)

4 激活函数层的实现

先来实现激活函数的ReLU层和Sigmoid层的实现

4.1 ReLU层

激活函数ReLU由下式表示：                      y关于x的导数，如下式所示：

           

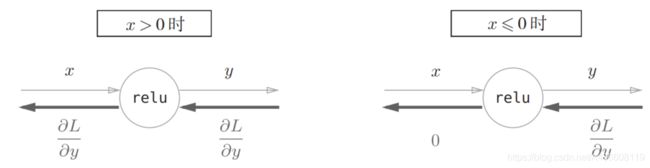
如果正向传播时的输入x大于0，则反向传播会将上游的值原封不动地传给下游。反过来，如果正向传播时的x小于等于0，则反向传播中传给下游的信号将停在此处。用计算图表示的话如下图所示

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

Relu类有实例变量mask。这个变量mask是由True/False构成的NumPy数组，它会把正向传播时的输入 x的元素中小于等于0的地方保存为 True，其他地方（大于0的元素）保存为 False。如下例所示， mask变量保存了由 True/False构成的NumPy数组

正向传播时的输入值小于等于0，则反向传播的值为0。因此，反向传播中会使用正向传播时保存的 mask，将从上游传来的 dout的mask中的元素为True的地方设为0。
 

4.2 Sigmoid层

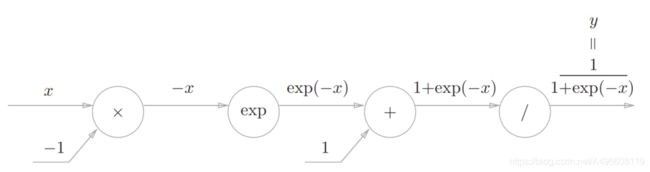
实现sigmoid函数的公式如下：

步骤1：

“/”节点表示

 

步骤2：

“+”节点将上游的值原封不动地传给下游

步骤3：

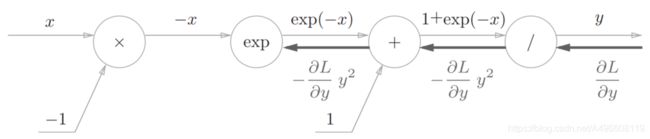
“exp”节点表示y = exp(x)，它的导数由下式表示。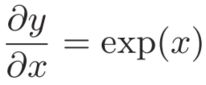

步骤4：

×”节点将正向传播时的值翻转后做乘法运算。因此，这里要乘以-1。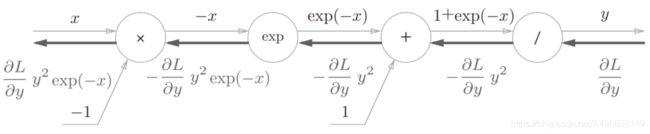

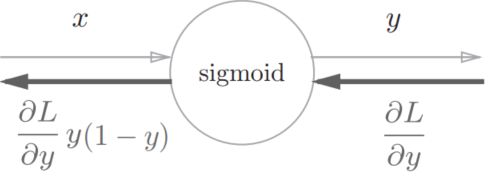
集约化的“sigmoid”节点：
 

                                

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

5 Affine/Softmax层的实现

5.1 Affine层

复习下神经网络正向传播的流程：

这里， X、 W、 B 分别是形状为(2,)、 (2, 3)、 (3,)的多维数组。这样一来，神经元的加权和可以用 Y = np.dot(X, W) + B计算出来。然后， Y 经过激活函数转换后，传递给下一层。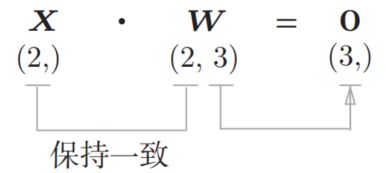

矩阵的乘积运算中对应维度的元素个数要保持一致
 

神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换” 。因此，这里将进行仿射变换的处理实现为“Affine层”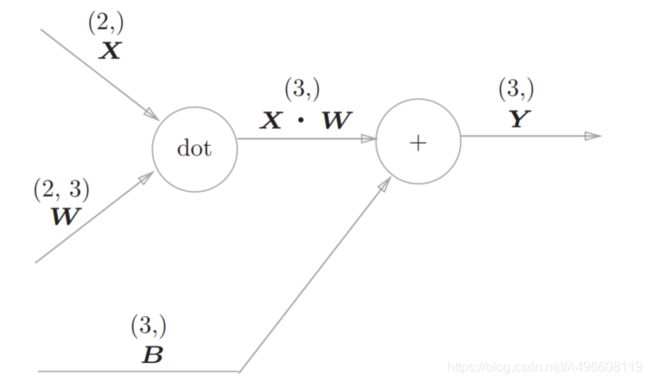

Affine层的计算图（注意变量是矩阵，各个变量的上方标记了该变量的形状）
接下来看下反向传播的推导：

中的T表示转置。转置操作会把W的元素(i, j)换成元素(j, i)。用数学式表示的话，可以写成下面这样。

5.2 批版本的Affine

前面介绍的Affi ne层的输入X是以单个数据为对象的。现在我们考虑N个数据一起进行正向传播的情况，也就是批版本的Affine层。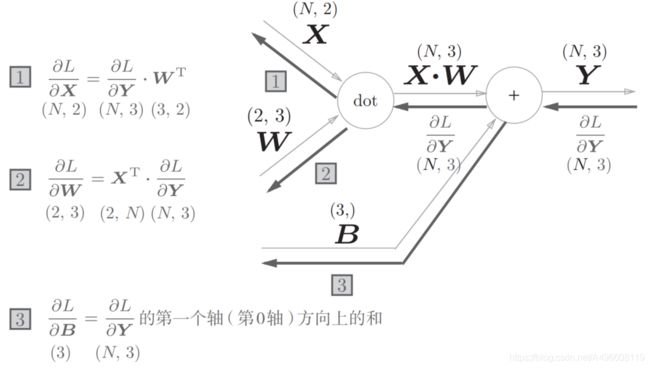

正向传播时，偏置会被加到每一个数据（第1个、第2个……）上。因此，反向传播时，各个数据的反向传播的值需要汇总为偏置的元素。用代码表示的话，如下所示。

综上所述， Affine的实现如下所示：另外， Affine的实现考虑了输入数据为张量（四维数据）的情况，与这里介绍的稍有差别。
 

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b
        
        self.x = None
        self.original_x_shape = None
        # 权重和偏置参数的导数
        self.dW = None
        self.db = None

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx

5.3 Softmax-with-Loss层

softmax函数会将输入值正规化之后再输出。比如手写数字识别时， Softmax层的输出如下图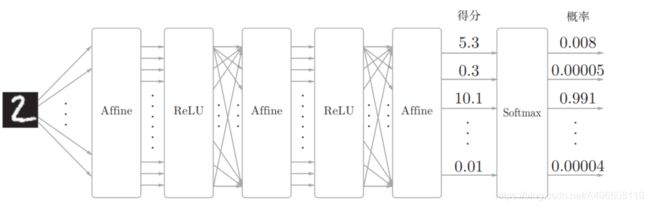

输入图像通过Affi ne层和ReLU层进行转换， 10个输入通过Softmax层进行正规化。在这个例子中，“ 0”的得分是 5.3，这个值经过Softmax层转换为 0.008（ 0.8%）；“ 2”的得分是10.1，被转换为0.991（ 99.1%）

神经网络中进行的处理有推理（inference）和学习两个阶段。神经网络的推理通常不使用Softmax层。比如，用图5-28的网络进行推理时，会将最后一个 Affine层的输出作为识别结果。神经网络中未被正规
化的输出结果（图 5-28中 Softmax层前面的 Affine层的输出）有时被称为“得分”。也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要Softmax层。
不过，神经网络的学习阶段则需要Softmax层。
 

下面来实现Softmax层。考虑到这里也包含作为损失函数的交叉熵误差（cross entropy error），所以称为“Softmax-with-Loss层”。 Softmax-withLoss层（Softmax函数和交叉熵误差）的计算图如下图所示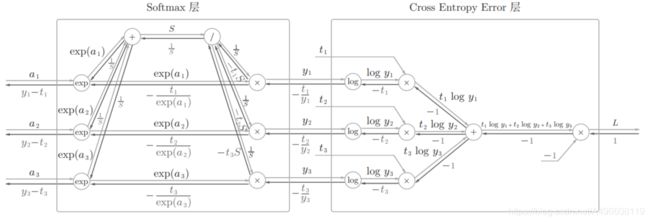

“简易版”的Softmax-with-Loss层的计算图
 

注意的是反向传播的结果。 Softmax层的反向传播得到了（y1 - t1, y2 - t2, y3 - t3）这样“漂亮”的结果。由于（y1, y2, y3）是Softmax层的输出，（t1, t2, t3）是监督数据，所以（y1 - t1, y2 - t2, y3 - t3）是Softmax层的输出和教师标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层，这是神经网络学习中的重要性质
神经网络学习的目的就是通过调整权重参数，使神经网络的输出（Softmax的输出）接近教师标签。因此，必须将神经网络的输出与教师标签的误差高效地传递给前面的层。刚刚的（y1 - t1, y2 - t2, y3 - t3）正是Softmax层的输出与教师标签的差，直截了当地表示了当前神经网络的输出与教师标签的误差。
这里考虑一个具体的例子，比如思考教师标签是（0, 1, 0）， Softmax层的输出是(0.3, 0.2, 0.5)的情形。因为正确解标签处的概率是0.2（20%），这个时候的神经网络未能进行正确的识别。此时， Softmax层的反向传播传递的是(0.3, -0.8, 0.5)这样一个大的误差。因为这个大的误差会向前面的层传播，所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。
再举一个例子，比如思考教师标签是(0, 1, 0)， Softmax层的输出是(0.01,0.99, 0)的情形（这个神经网络识别得相当准确）。此时Softmax层的反向传播传递的是(0.01, -0.01, 0)这样一个小的误差。这个小的误差也会向前面的层传播，因为误差很小，所以Softmax层前面的层学到的内容也很“小”。

现在来进行Softmax-with-Loss层的实现，实现过程如下所示。
 

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx

6 误差反向传播的实现

之前介绍的误差反向传播法会在步骤2中出现