CoIL:Coordinate-Based Internal Learning for Tomographic Imaging

CoIL:Coordinate-Based Internal Learning for Tomographic Imaging

标题基于坐标神经表示的断层成像

作者：竹石
来源：Cooridnate-based-Internal-Learning

1. 导读

CoIL的全称是Coordinate-Based Internal Learning for Tomographic Imaging，基于坐标神经表示的断层成像，其核心是MLP，它将投影坐标映射到相应的传感器响应。除了测试对象本身的投影外，不需要其他数据。训练MLP后，CoIL生成可用于大多数图像重建方法的新投影值。CoIL是一种自监督方法，是一种连续表示的投影场(文中写的是measurement fields,翻译成投影场是更合适)。
这种single-shot方案有利于无法获得完全采样数据的应用。例如，在CT中，表征响应的两个参数是入射光线束的视角和相关探测器在传感器平面上的空间位置。在投影数据中提取的坐标响应来训练MLP，CoIL能建立坐标到传感器响应的连续映射。因此，MLP对应整个投影场的神经表示，通过查询具有相关坐标，可以生成该坐标下的投影。图1，稀疏视图CT背景下CoIL的概念图。
图1，稀疏视图CT背景下CoIL的概念图。多层感知器（MLP）通过学习将投影坐标(θ,l)映射到其响应r来表示整个投影场。比较了有CoIL和没有CoIL的总变异（TV）恢复的图像。CoIL被用来从由120个输入信噪比为40dB的噪声视图组成的数据中生成360个视图。注：wo：without没有，w：with有

文章的贡献如下：

• 提出CoIL作为一种新的成像方法，利用CoIL来估计高保真投影场，CoIL侧重于表示未知的对象，可以在重建过程中与其他信息源组合。
• 提出了一种新的MLP架构，该架构对网络的输入坐标使用线性映射策略。相较位置编码[1]和随机采样[2]，这种映射策略对表征投影场是有效的，并实现了更好的性能。
• 在稀疏视图CT环境中广泛验证了我们的方法。表明CoIL通过能够生成高保真全视正弦图，与大多数广泛使用的方法可以协同结合。文中的所有实验验证了，使用CoIL的方法始终优于不使用CoIL的方法。

2. CoIL方法

在本节中，详细介绍CoIL方法，该方法是基于坐标学习的神经场来解决成像逆问题。图2说明了 CoIL 的一般工作流程。首先解释所提出的 MLP 网络，然后讨论其与几种常见图像重建方法的集成。

图 2. 具有自由参数$v\in R^v$的断层成像系统的 CoIL 工作流程示意图。首先，系统在v的不同实现下获得一组 N>0投影值。然后，坐标-响应对 ${(v_i,r_i)}_{(i=1)}^N$ 用于训练基于坐标的MLP $M_{\phi }:v\to r$ 用于对整个投影场进行训练。训练完成后，通过查询相关坐标以任意分辨率从 $M_{\phi }$ 中提取编码字段。在最后阶段，CoIL输出的投影值和真实值共同用于图像重建。

2.1Measurement-Field Encoding With MLP

基于坐标的MLP是CoIL的中心组件，网络可以表示为：
$${\mathcal{M}}_{\varphi }:\mathbf{v}\to r\text{ with }\mathbf{v}\in {\mathbb{R}}^v,r\in \mathbb{R}$$其中$v$表示给定成像系统中的坐标，$r$表示相应的传感器响应。该网络在概念上可以分为两部分:第一部分是傅立叶特征映射（Fourier feature mapping, FFM）层$\gamma (v)$，即训练前预定义。第二部分是标准MLP $N_{\phi }:\gamma (v)\to r$，即参数$\phi$的训练。

1) Fourier Feature Mapping:

标准 MLP 在表示高频变化方面表现不佳[1]、[3]。为了克服标准 MLP 的限制，我们将输入坐标 v扩展为不同频率分量的组合
$$\gamma (\mathbf{v})=\left(\begin{array}{c}\sin \left(k_1\pi \mathbf{v}\right),\cos \left(k_1\pi \mathbf{v}\right)\\ ⋮\\ \sin \left(k_L\pi \mathbf{v}\right),\cos \left(k_L\pi \mathbf{v}\right)\end{array}\right)$$其中sin⁡和cos⁡分别计算元素正弦值和余弦值，${k_i}_{(i=1)}^L$确定映射中的频率。 FFM 层预先定义了频率分量，以便网络 $N_{\phi }$可以通过学习第一层的权重来主动选择对编码传感器响应最有用的频率分量。通过操纵系数 $k_i$ 和组件总数 $L>0$，我们可以显式地控制扩展频谱，从而施加一些隐式正则化。
FFM 层首先在 NeRF 中作为空间坐标的位置编码[1] 被引入，随后的工作[4]通过使用称为神经切线核[5]的概念进一步探索了它的功能。[1]中$\gamma (v)$的原始公式将 $k_i$设置为指数函数 $k_i=2^{(i-1)}，L=10$。
我们发现very high-frequency 非常高的高频分量会导致 MLP 对噪声的过度拟合。因此，我们在傅里叶空间中采用了线性采样 $k_i=\pi i/2$，这导致低频区域中的频率分量数量过多。如图5所示，我们的经验结果表明，我们的策略可以有效地提高 $M_{\phi }$ 在表示高频变化，并能防止过度拟合噪声方面的效果。

2)MLP Architecture:

图3 CoIL完整网络架构图示。网络$M_{\phi }=N_{\phi }\circ \gamma (v)$是傅立叶特征映射(FFM)层$\gamma (v)$和传统MLP $N_{\phi }$的级联。作为示例对${(v_i,r_i)}_{(i=1)}^N$的训练，$M_{\phi }$能够学习从坐标到其响应$r$的连续映射。因此 $M_{\phi }$成为完整投影场的隐式神经表示。

实现$N_{\phi }$的网络架构由17个全连接（FC）层组成。前16层有256个隐藏神经元由ReLU激活，最后一层有128个隐藏神经元没有任何激活。在每个偶数（少于16个）FC层之后存在7个跳过连接，以将$N_{\phi }$的输入与中间输出连接起来。使用跳跃连接已被证明有利于快速训练[6]和更好的准确性[7]。
请注意，尽管$M_{\phi }$是一个完全连接的网络，但它的输入对应于单个坐标，从而可以对所有投影进行逐元素处理。
CoIL 训练一个单独的 MLP 来代表每个测试对象的完整投影场。这意味着训练对 ${(v_i,r_i)}_{(i=1)}^N$是仅提取测试对象的投影值来获得的，没有任何训练数据集。通过使用 Adam [8] 训练网络 $M_{\phi }$，以最小化标准$l_2$范数损失，
$$\ell (\psi )=\frac{1}{N}\sum _{i=1}^N{\Vert {\mathcal{M}}_{\varphi }\left({\mathbf{v}}_i\right)-r_i\Vert }_2^2$$
实现了一个递减的学习率，它随着训练时间的增加呈指数衰减。M_φ网络权重也比较小，约占4.2 MB。

2.2 Image Reconstruction in CoIL

训练后，可以通过使用相关坐标查询 $M_{\phi }$来生成任意数量的投影值。我们将相应的投影字段称为 CoIL 字段。我们讨论了将 CoIL 集成到四种广泛使用的方法中：

1)线性重建：

滤波反投影（FBP）是将投影值带入图像域的经典方法[9]。由于 CoIL 场本质上是一组投影值，我们可以直接将场作为输入提供给 FBP 以进行图像重建。应用 FBP 的一种不同的方法是形成一个组合输入，其中包括原始投影和CoIL生成的投影。后一种方法的主要好处是它直接使用真实数据，同时还补充了由 CoIL 投影生成的数据。

2)基于模型的优化：

基于模型的方法通过解决形式，
$$\mathbf{x}=\underset{\mathbf{x}\in {\mathbb{R}}^n}{\mathrm{argmin}}f(\mathbf{x}),\text{ with }f(\mathbf{x})=g(\mathbf{x})+h(\mathbf{x})$$的优化问题来重建图像。通过在目标函数中附加的“数据保真度”项g ̃，可以将CoIL场结合到公式中：
$$f(\mathbf{x})=\underset{\text{New data-fidelity }}{(1-\alpha )g(\mathbf{x})+\alpha \tilde{g}(\mathbf{x})}+h(\mathbf{x})$$
参数$0\le \alpha \le 1$控制真实数据和生成场之间的tradeoff权衡。在实践中，我们可以微调α的值，以在两项之间获得良好的平衡。例如，考虑最小平方函数：
$$\tilde{g}(\mathbf{x})=\frac{1}{2}{\Vert \tilde{\mathbf{A}}\mathbf{x}-{\mathcal{M}}_{\varphi }(\tilde{\mathbf{v}})\Vert }_2^2$$
其中$\tilde{A}\in R^{(m\times n)}$对应CoIL field的采样几何，$\tilde{v}$ 表示训练后的MLP $M_{\phi }(\tilde{v})$的所有query coordinates查询坐标。由于网络是预训练的，因此可以直接使用任何现有的image regularizer图像正则化器，并使用标准迭代算法（如FISTA或ADMM）来解决优化问题。

3)End-to-End Deep-Learning(DL) Models:

大多数end-to-end DL模型直接将低质量图像${{\tilde{x}}_i}_{(i=1)}^N$映射到高质量图像${x_i}_{(i=1)}^N$进行训练，使它们vulnerable to unseen outliers容易受到看不见的异常值的影响。
例如，当训练和测试角度不匹配时，这会对DL的性能产生不利影响。CoIL可以通过生成与用于训练DL模型的投影值对应的子采样率相同的投影值字段来解决这个问题：
$$\mathbf{x}={\mathcal{F}}_{\psi }\left(\mathrm{FBP}\left({\mathcal{M}}_{\varphi }(\tilde{\mathbf{v}})\right)\right)$$其中$F_{\psi }$表示预训练的CNN。另外, 可以在输入中加入原始测试图像，通过使用权重α来加权$\tilde{x}$ 和$FBP(M_{\phi }(\tilde{v}))$：
$$\mathbf{x}={\mathcal{F}}_{\psi }(\underset{\text{Joint input }}{(1-\alpha )\tilde{\mathbf{x}}+\alpha \mathrm{FBP}\left({\mathcal{M}}_{\varphi }(\tilde{\mathbf{v}})\right)})$$这种方法使MLP学习到的投影值与真实投影值一起使用。文章中的实验结果也表明，这种基于CoIL的策略比直接在投影值上训练DL模型取得了更好的结果。

4)Denoising-Driven Approches:

PnP/RED算法可以被解释为基于模型的算法的扩展，平衡与投影结果的一致性和深度去噪先验[22],[25]。考虑基于梯度的RED(GM-RED)：
$${\mathbf{x}}^{+}\leftarrow \mathbf{x}-\gamma \left[\nabla g(\mathbf{x})+\tau \left(\mathbf{x}-{\mathcal{D}}_{\sigma }(\mathbf{x})\right)\right]$$其中γ>0是步长，∇g是数据保真度项的梯度。
与基于模型的优化的修改类似，将CoIL整合到GM-RED中的一个直接的方法是将g ̃的梯度作为一个额外的项包括在内：
$${\mathbf{x}}^{+}\leftarrow \mathbf{x}-\gamma [\underset{\text{New data enforcement }}{(1-\alpha )\nabla g(\mathbf{x})+\alpha \nabla \tilde{g}(\mathbf{x})}+\tau \left(\mathbf{x}-{\mathcal{D}}_{\sigma }(\mathbf{x})\right)]$$其中，新的更新确保了与实际投影以及CoIL场生成的投影值的一致性，α控制相对加权。这个想法也适用于PnP，例如，通过将CoIL整合到PnP-FISTA中。
$$\begin{array}{rl}& {\mathbf{x}}^{+}\leftarrow {\mathcal{D}}_{\sigma }(\mathbf{s}-\gamma [(1-\alpha )\nabla g(\mathbf{s})+\alpha \nabla \tilde{g}(\mathbf{s})])\\ & {\mathbf{s}}^{+}\leftarrow {\mathbf{x}}^{+}+\left(\left(q^{+}-1\right)/q^{+}\right)\left({\mathbf{x}}^{+}-\mathbf{x}\right)\end{array}$$此时， the acceleration parameter加速参数q>0被更新为，
$$q^{+}\leftarrow \frac{1}{2}\left(1+\sqrt{1+4q^2}\right)$$

3. 实验&总结

文章的实验是配备了Intel Xeon Gold 6130处理器和四个Nvidia GeForce GTX 1080 Ti GPU的机器上进行了所有的实验，以及所有神经网络的训练。在这台机器上使用一个GPU训练一个MLP大约需要30分钟。
图 8. 使用几种方法在有和没有 CoIL 的情况下重建的可视化图示。 CoIL 生成对应于 360（用于 FBP、TV 和 RED）和 90（用于 FBP-UNet）视图的测量场，来自 P = 6 0 测量，I = 4 0 dB 噪声。每个图像都标有其相对于最左侧列中显示的地面实况的 SNR 值。使用绿色箭头在边界框中突出显示视觉差异。注意 CoIL 如何在没有它的情况下恢复重建中丢失的某些细节。

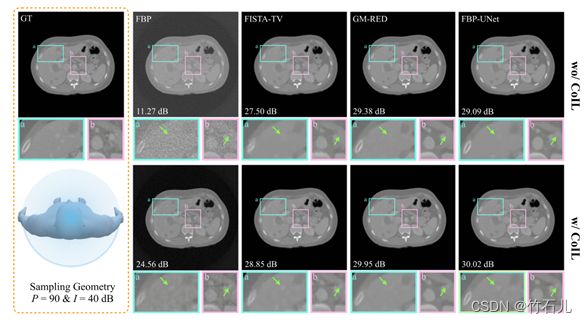
图 9. 使用几种方法在有和没有 CoIL 的情况下重建的可视化图示。 CoIL 生成对应于 360（用于 FBP、TV 和 RED）和 135（用于 FBP-UNet）视图的测量场，来自 P = 9 0 测量，I = 4 0 dB 噪声。每个图像都标有其相对于最左侧列中显示的地面实况的 SNR 值。使用绿色箭头在边界框中突出显示视觉差异。

图10. 使用几种方法在有和没有 CoIL 的情况下重建的可视化图示。 CoIL 从 P=120 次测量中生成对应于 360（用于 FBP、TV 和 RED）和 180（用于 FBP-UNet）视图的测量场，其中I=40dB 噪声。每个图像都标有其相对于最左侧列中显示的地面实况的 SNR 值。使用绿色箭头在边界框中突出显示视觉差异。
本文开发的 CoIL 方法是一种利用基于坐标的神经表示的新计算成像方法。CoIL 试图将整个测量场表示为经过训练的单个 MLP 网络，以将测量坐标映射到其传感器响应。这使得 CoIL 成为一种自我监督模型，无需任何外部数据集即可进行训练。这里提供的大量实证结果证明了 CoIL 在稀疏视图 CT 的背景下的改进，突出了其与现有图像重建方法协同工作的巨大潜力。
CoIL 的潜在局限性。一个限制是训练 MLP 的计算开销，当集成到整个成像管道中时，可以显着降低图像形成的速度。这个问题的部分解决方案是在多个 GPU 上并行化 MLP 训练，从而减少 CoIL 训练开销。另一种局限性在于，通过生成额外的投影值，来进行重建，会增加图像重建算法的每次迭代复杂度。这表明必须平衡合成投影的数量，以在计算限制下实现最佳成像性能。

4. 参考文献

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis, Cham, F, 2020 [C]. Springer International Publishing.
[2] Tancik M, Srinivasan P P, Mildenhall B, et al. Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains [J]. ArXiv, 2020, abs/2006.10739(
[3] Rahaman N, Baratin A, Arpit D, et al. On the spectral bias of neural networks; proceedings of the International Conference on Machine Learning, F, 2019 [C]. PMLR.
[4] Tancik M, Srinivasan P, Mildenhall B, et al. Fourier features let networks learn high frequency functions in low dimensional domains [J]. Advances in Neural Information Processing Systems, 2020, 33(7537-47.
[5] Jacot A, Gabriel F, Hongler C. Neural tangent kernel: Convergence and generalization in neural networks [J]. Advances in neural information processing systems, 2018, 31
[6] Chen Z, Zhang H. Learning implicit fields for generative shape modeling; proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, F, 2019 [C].
[7] Park J J, Florence P, Straub J, et al. Deepsdf: Learning continuous signed distance functions for shape representation; proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, F, 2019 [C].
[8] Kingma D P, Ba J. Adam: A method for stochastic optimization [J]. arXiv preprint arXiv:14126980, 2014,
[9] Kak A C, Slaney M. Principles of computerized tomographic imaging [M]. SIAM, 2001.