深度学习之图像分类（三）--AlexNet网络结构

深度学习之图像分类（三）AlexNet网络结构

从本节开始，将逐个讲述图像分类模型的发展历程，首个就是 AlexNet，学习视频源于 Bilibili，感谢霹雳吧啦Wz，建议大家去看视频学习哦。

1. 前言

AlexNet 是 2012 年 ISLVRC2012 (Image Large Scale Visual Recognition Challenge) 竞赛的冠军网络，原始论文为 ImageNet Classification with Deep Convolutional Neural Networks。当时传统算法已经达到性能瓶颈，然而 AlexNet 将分类准确率由传统的 70%+ 提升到 80%+。它是由 Hinton 和他的学生 Alex Krizhevsky 设计的。也就是在那年之后，每年的 ImageNet LSVRC 挑战赛都被深度学习模型霸占着榜首，深度学习开始迅速发展。

ISLVRC2012 包括以下三部分：

• 训练集：1281167 张已标注图片
• 验证集：50000 张已标注图片
• 测试集：100000 张未标注图片

它有以下几个亮点：

• 首次使用 GPU 进行网络加速训练
  • 1998年的 LeNet 受限于硬件没有引起重
  • 尽管当初使用了 GPU，但是他们用 5-6 天训练了这个模型，并且限制了网络的大小
• 使用了 ReLU 激活函数，而不是传统的 Sigmoid 激活函数以及 Tanh 激活函数
  • Sigmoid 等激活函数求导比较麻烦
  • Sigmoid 等激活函数当网络比较深的时候会出现梯度消失
• 使用了 LRN 局部响应归一化
• 使用了数据增强
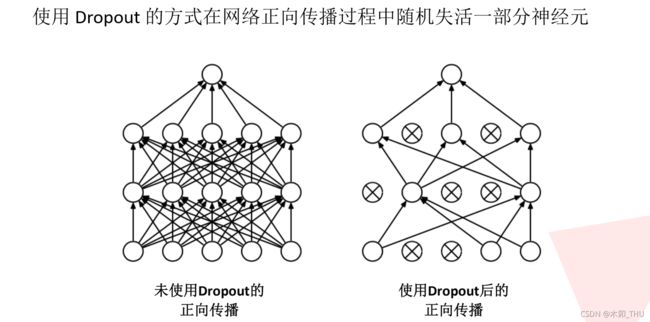
• 在全连接层的前两层中使用了 Dropout 随机失活神经元操作，以减少过拟合现象
  • 使用 Dropout 的方式在网络正向传播过程中随机失活一部分神经元

在具体讲解网络结构之前，补充卷积公式。经过卷积后的矩阵尺寸大小计算公式为：$N=(W-F+2P)/S+1$。

• 输入图片大小为 $W\times W$
• 卷积核 Filter 大小为 $F\times F$
• 步长 stride 为 $S$
• (半边) padding 的像素数为 $P$

2. 网络结构

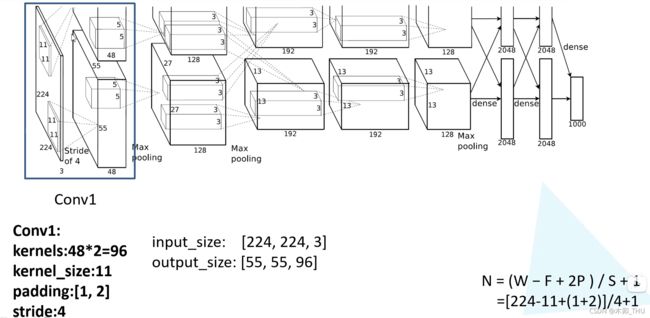
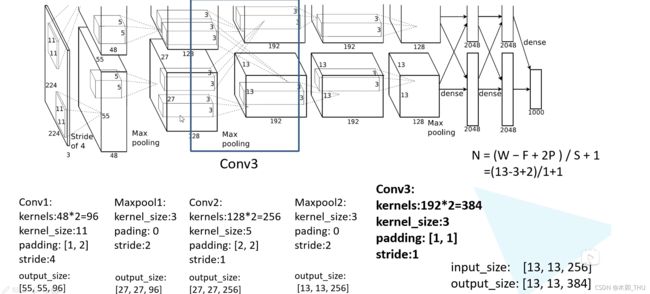
AlexNet 网络结构如下所示：

因为原作者使用两块 GPU 并行训练，所以画了一摸一样的两行，其实我们看其中一行就可以了。网络第一层可以看到，原始图像为 $224\times 224\times 3$ 的 RGB 彩色图像。网络第一层为 $11\times 11$ 大小卷积核的卷积层，卷积核个数为 96。第一层卷积之后的输出为 $55\times 55\times 96$，所以我们可以反推出 padding = [1, 2]，左边上边加一列 0，右边下边加两列 0。

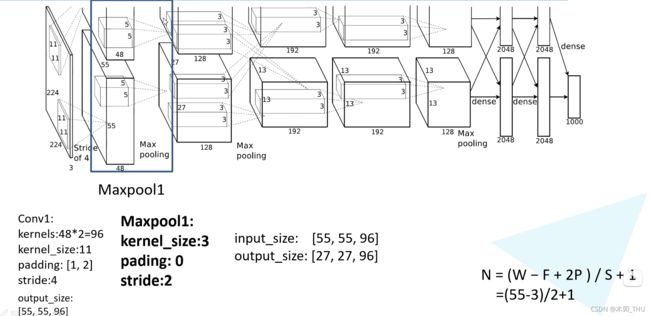
然后就是经过了一个 Maxpooling 层，kernel size 为 $3\times 3$，padding = 0，stride = 2。此后的输出就是 $27\times 27\times 96$。（原始论文并没有提到 padding 和 stride 这些细节，但是看官方实现可以了解到）

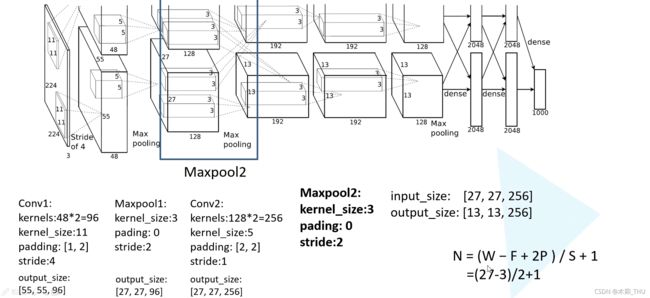
然后又是一个卷积层，输出通道为 256，kernel size 为 5，padding 为 [2,2]，stride = 1。可以计算得到输出特征图为 $27\times 27\times 256$。

然后就是经过了一个 Maxpooling 层，kernel size 为 $3\times 3$，padding = 0，stride = 2。此后的输出就是 $13\times 13\times 256$。

接下来是第三个卷积层，输出通道为 384，kernel size 为 $3\times 3$，padding = 1，stride = 1，也就是保大小的卷积。输出特征图为 $13\times 13\times 384$。

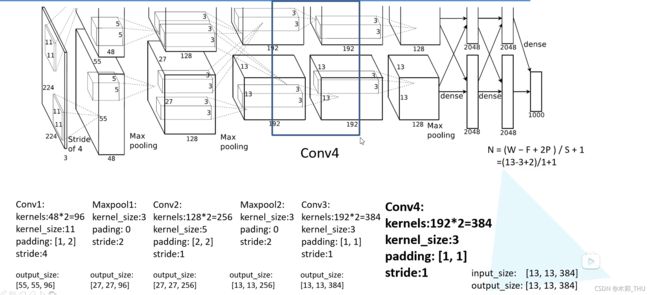
第四个卷积层和第三个卷积层是一模一样的，只不过输入通道从 256 变成了 384。输出特征图为 $13\times 13\times 384$。

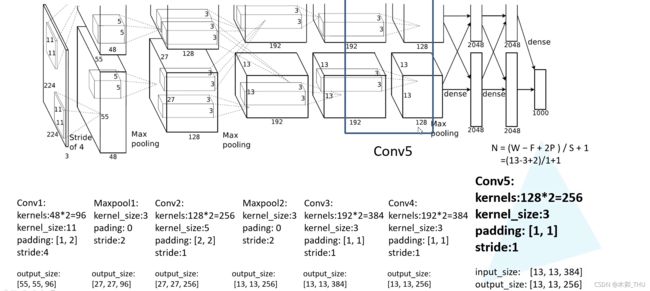
第五个卷积层输出通道为 256，kernel size 为 $3\times 3$，padding = 1，stride = 1，也是保大小的卷积。输出特征图为 $13\times 13\times 256$。

之后经过了一个 Maxpooling 层，kernel size 为 $3\times 3$，padding = 0，stride = 2。此后的输出就是 $6\times 6\times 256$。

此后就展平特征图，经过两个 4096 个节点的全连接层，最后再通过一个 1000 个节点（ImageNet 是 1000 分类）的全连接层获得输出就可以了。注意到，所有卷积层后面其实都接了一个激活函数 ReLU 层。在全连接层的前两层中使用了 Dropout 随机失活神经元操作。

3. 其他细节

本章节参考博文 深入理解AlexNet网络，并加入了部分个人理解。

3.1 Local Response Normalization (局部响应归一化)

在神经网络中，我们用激活函数将神经元的输出做一个非线性映射，但是 tanh 和 sigmoid 这些传统的激活函数的值域都是有范围的，但是 ReLU 激活函数得到的值域没有一个区间，所以要对 ReLU 得到的结果进行归一化。也就是 Local Response Normalization。局部响应归一化的方法如下面的公式：
$$b_{(x,y)}^i=\frac{a_{(x,y)}^i}{{\left(k+\alpha {\sum }_{j=\max (0,i-n/2)}^{\min (N-1,i+n/2)}{\left(a_{(x,y)}^j\right)}^2\right)}^{\beta }}$$
在公式中，$a_{(x,y)}^i$ 代表的是 ReLU 在第 i 个 kernel 的 (x, y) 位置的输出，n 表示的是，$a_{(x,y)}^i$ 的邻居个数，N 表示该 kernel 的总数量。$b_{(x,y)}^i$ 表示的是 LRN 的结果。ReLU 输出的结果和它周围一定范围的邻居做一个局部的归一化，这里有点类似域我们的最大最小归一化，即假设有一个向量 $X=[x_1,x_2,...,x_n]$，那么将所有的数归一化到 0-1 之间的归一化规则是 $x_i=(x_i-x_{min})/(x_{max}-x_{min})$。而上面的式子则是在通道层面进行归一化，有一些其他的参数 $\alpha ,\beta ,k$。论文中说在验证集中确定，最终确定的结果为：$k=2,n=5,\alpha =10^{-4},\beta =0.75$。

上图，每一个矩形表示的一个卷积核生成的 feature map。所有的元素已经经过了 ReLU 激活函数，现在我们都要对具体的 pixel 进行局部的归一化。假设绿色箭头指向的是第 i 个 kernel 对应的特征图，其余的四个蓝色箭头是它周围的邻居 kernel 层对应的特征图，假设矩形中间的绿色的元素的位置为 (x, y)，那么我需要提取出来进行局部归一化的数据就是周围邻居 kernel 对应的特征图的 (x, y) 位置的 pixel 的值。也就是上面式子中 $a_{(x,y)}^j$ 。然后把这些邻居元素的值平方再加和。乘以一个系数 $\alpha$ 再加上一个常数 k (防止分母为 0)，然后 $\beta$ 次幂，最终得到分母。分子就是第 i 个 kernel 对应的特征图的 (x, y) 位置的元素值。

但是我觉得，这有个假设在于连续通道之间有一定的关系，然而我们知道，卷积层中连续通道不一定有”连续“意义，就像全连接层中相邻节点一样。所以这样的领域有待进一步思考！

3.2 Overlapping Pooling (覆盖的池化操作)

一般的池化层因为没有重叠，所以 pool size 和 stride 一般是相等的，例如 8 × 8 的一个图像，如果池化层的尺寸是 2 × 2，那么经过池化后的操作得到的图像是 4 × 4 大小的，这种设置叫做不覆盖的池化操作。如果 stride < pool size, 那么就会产生覆盖的池化操作，这种有点类似于 convolutional 化的操作，这样可以得到更准确的结果。甚至在之前讲述的 YOLOv3 的 SPP 模块中，使用 stride 为 1 的 maxpooling，我其实认为获得的是超像素！下图以图像超像素为例：

超像素最直观的解释，便是把一些具有相似特性的像素“聚合”起来，形成一个更具有代表性的大“元素”。而这个新的元素，将作为其他图像处理算法的基本单位。

论文中说，在训练模型过程中，覆盖的池化层更不容易过拟合。在 top-1，和 top-5 中使用覆盖的池化操作分别将 error rate 降低了 0.4% 和 0.3%。

3.3 Data Augmentation (数据增强)

文章使用 Random Crop、flip 从而上千倍的扩充训练样本的数量，也使得随机裁剪成为通用方法。具体做法就是首先将图片 resize 到 256 x 256大小，然后从中随机裁剪出 224 x 224 大小的 patch 训练，测试时就从四个角及中心 crop，然后水平翻转图像形成 10 个测试图片，然后对于这 10 个结果取一下平均值（这种方法在后来的去马赛克任务中也有用，将图片顺时针转动四次，然后恢复结果转动回来取平均，其实有点模型集成投票的意思，避免了训练多个模型）。另一种增强为转换RGB 通道的强度，在之后的模型中很少用到。对于该模型，数据增强大约降低了 1% 错误率。

4. 代码

import torch.nn as nn
import torch


class AlexNet(nn.Module):
    def __init__(self, num_classes=1000, init_weights=False):
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 96, kernel_size=11, stride=4, padding=2),  # input[3, 224, 224]  output[48, 55, 55]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[96, 27, 27]
            nn.Conv2d(96, 256, kernel_size=5, padding=2),           # output[256, 27, 27]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[256, 13, 13]
            nn.Conv2d(256, 384, kernel_size=3, padding=1),          # output[384, 13, 13]
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 384, kernel_size=3, padding=1),          # output[384, 13, 13]
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),          # output[256, 13, 13]
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),                  # output[256, 6, 6]
        )
        self.classifier = nn.Sequential(
            nn.Dropout(p=0.5),
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Dropout(p=0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        x = self.features(x)
        x = torch.flatten(x, start_dim=1)
        x = self.classifier(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)