【Python数据可视化(二)】数据导入

文件与异常

  在Python中实现文件的读写操作其实非常简单，通过Python内置的open函数，我们可以指定文件名、操作模式、编码信息等来获得操作文件的对象，接下来就可以对文件进行读写操作了。

操作模式	具体含义
'r'	读取 （默认）
'w'	写入（会先截断之前的内容）
'x'	写入，如果文件已经存在会产生异常
'a'	追加，将内容写入到已有文件的末尾
'b'	二进制模式
't'	文本模式（默认）
'+'	更新（既可以读又可以写）

  读取文本文件时，需要在使用open函数时指定好带路径的文件名（可以使用相对路径或绝对路径）并将文件模式设置为'r'（如果不指定，默认值也是'r'），然后通过encoding参数指定编码（如果不指定，默认值是None，那么在读取文件时使用的是操作系统默认的编码），如果不能保证保存文件时使用的编码方式与encoding参数指定的编码方式是一致的，那么就可能因无法解码字符而导致读取失败。如果open函数指定的文件并不存在或者无法打开，那么将引发异常状况导致程序崩溃。为了让代码有一定的健壮性和容错性，可以使用Python的异常机制对可能在运行时发生状况的代码进行适当的处理——可以将那些在运行时可能会出现状况的代码放在try代码块中，在try代码块的后面可以跟上一个或多个except来捕获可能出现的异常状况。例如在上面读取文件的过程中，文件找不到会引发FileNotFoundError，指定了未知的编码会引发LookupError，而如果读取文件时无法按指定方式解码会引发UnicodeDecodeError，我们在try后面跟上了三个except分别处理这三种不同的异常状况。最后我们使用finally代码块来关闭打开的文件，释放掉程序中获取的外部资源，由于finally块的代码不论程序正常还是异常都会执行到（甚至是调用了sys模块的exit函数退出Python环境，finally块都会被执行，因为exit函数实质上是引发了SystemExit异常），因此我们通常把finally块称为“总是执行代码块”，它最适合用来做释放外部资源的操作。如果不愿意在finally代码块中关闭文件对象释放资源，也可以使用上下文语法，通过with关键字指定文件对象的上下文环境并在离开上下文环境时自动释放文件资源。

文件读取

def main():
    f = None
    try:
        f = open('123.txt', 'r', encoding='utf-8')
        print(f.read())
    except FileNotFoundError:
        print('无法打开指定的文件!')
    except LookupError:
        print('指定了未知的编码!')
    except UnicodeDecodeError:
        print('读取文件时解码错误!')
    finally:
        if f:
            f.close()


if __name__ == '__main__':
    main()

等价于

def main():
    try:
        with open('123.txt', 'r', encoding='utf-8') as f:
            print(f.read())
    except FileNotFoundError:
        print('无法打开指定的文件!')
    except LookupError:
        print('指定了未知的编码!')
    except UnicodeDecodeError:
        print('读取文件时解码错误!')


if __name__ == '__main__':
    main()

  除了使用文件对象的read方法读取文件之外，还可以使用for-in循环逐行读取或者用readlines方法将文件按行读取到一个列表容器中。

import time


def main():
    # 一次性读取整个文件内容
    with open('123.txt', 'r', encoding='utf-8') as f:
        print(f.read())

    # 通过for-in循环逐行读取
    with open('123.txt', mode='r') as f:
        for line in f:
            print(line, end='')
            time.sleep(0.5)
    print()

    # 读取文件按行读取到列表中
    with open('123.txt') as f:
        lines = f.readlines()
    print(lines)
    

if __name__ == '__main__':
    main()

文件写入

  要将文本信息写入文件文件也非常简单，在使用open函数时指定好文件名并将文件模式设置为'w'即可。如果要写入的文件不存在会自动创建文件而不是引发异常。注意如果需要对文件内容进行追加式写入，应该将模式设置为'a'。

from math import sqrt
	"""
	1-99之间的素数保存在a.txt中，100-999之间的素数保存在b.txt中，1000-9999之间的素数保存在c.txt中
	"""
def is_prime(n):
    """判断素数的函数"""
    assert n > 0
    for factor in range(2, int(sqrt(n)) + 1):
        if n % factor == 0:
            return False
    return True if n != 1 else False


def main():
    filenames = ('a.txt', 'b.txt', 'c.txt')
    fs_list = []
    try:
        for filename in filenames:
            fs_list.append(open(filename, 'w', encoding='utf-8'))
        for number in range(1, 10000):
            if is_prime(number):
                if number < 100:
                    fs_list[0].write(str(number) + '\n')
                elif number < 1000:
                    fs_list[1].write(str(number) + '\n')
                else:
                    fs_list[2].write(str(number) + '\n')
    except IOError as ex:
        print(ex)
        print('写文件时发生错误!')
    finally:
        for fs in fs_list:
            fs.close()
    print('操作完成!')


if __name__ == '__main__':
    main()

读写二进制文件

"""
实现图片复制
"""
def main():
    try:
        with open('algorithm.jpg', 'rb') as fs1:
            data = fs1.read()
            print(type(data))  # 
        with open('algorithm_copy.jpg', 'wb') as fs2:
            fs2.write(data)
    except FileNotFoundError as e:
        print('指定的文件无法打开.')
    except IOError as e:
        print('读写文件时出现错误.')
    print('程序执行结束.')


if __name__ == '__main__':
    main()

读写JSON文件

  JSON是“JavaScript Object Notation”的缩写，本来是JavaScript语言中创建对象的一种字面量语法，现在被广泛的应用于跨平台跨语言的数据交换，因为JSON也是纯文本，任何系统任何编程语言处理纯文本都是没有问题的。目前JSON基本上已经取代了XML作为异构系统间交换数据的实施标准。

{
	"Data":"2020-12-8",
	"City":"上海",
	"Weather":"阴",
	"cars": [
        {"brand": "BYD", "max_speed": 180},
        {"brand": "Audi", "max_speed": 280},
        {"brand": "Benz", "max_speed": 320}
    ]
}

  Python中的json模块就可以将字典或者列表以json格式保存到文件中。json模块主要有四个比较重要的函数：

函数	解释
dump	将python对象按照json格式序列化到文件中
dumps	将python对象处理成json格式的字符串
load	将文件中的json数据反序列化成对象
loads	将字符串的内容反序列化成python对象

import json


def main():
    mydict = {
        "Data": "2020-12-8",
        "City": "上海",
        "Weather": "阴",
        "cars": [
            {"brand": "BYD", "max_speed": 180},
            {"brand": "Audi", "max_speed": 280},
            {"brand": "Benz", "max_speed": 320}
        ]
    }
    try:
        with open('data.json', 'w', encoding='utf-8') as fs:
            json.dump(mydict, fs)
    except IOError as e:
        print(e)
    print('保存数据完成!')


if __name__ == '__main__':
    main()

补充说明：
  序列化在计算机科学的数据处理中，是指数据结构或者对象状态转换为可以存储或传输的形式，这样在需要的时候能够恢复到原先的状态，而且通过序列化的数据重新获取字节时，可以利用这些字节来产生原始对象的副本。与这个过程相反的动作，即从一系列字节中提取数据结构的操作就是反序列化。

  使用request模块访问网络API获取数据，通过json模块解析JSON数据并显示新闻标题。

import requests
import json


def main():
    resp = requests.get('http://api.tianapi.com/guonei/?key='需要申请'')
    data_model = json.loads(resp.text)
    for news in data_model['newslist']:
        print(news['title'])


if __name__ == '__main__':
    main()

补充说明：
  APIKey申请需要到天行数据网站申请。

从CSV文件导入数据

  CSV是指逗号分隔的值，文件中还包括一个文件头，也是以逗号分隔的。在这里所用的ex.csv作为示例数据，你可以把它下载到本地，把示例数据和代码放在相同的目录下。

# 导入CSV模块以便访问所需的方法
import csv
import sys
filename = 'ex.csv'
data = []
try:
    # 打开ex.csv文件，用with语句打开数据文件并把它绑定到对象f，不必操心在操作完资源后去关闭数据文件
    # with语句的上下文管理器会帮助处理
    with open(filename,'rt') as f:
        reader = csv.reader(f)
        # 首先读取文件头
        header = next(reader)
        # 然后读取所有行
        data = [row for row in reader]
except csv.Error as e:
    print('ex.csv文件第{}行出现异常:{}'.format(reader.line_num,e))
    sys.exit(-1)
if header:
    print(header)
    print('=====================')
for datarow in data:
    print(datarow)

  运行效果：

补充说明：
  读取文件时一旦发生错误，csv.reader()方法会生成错误信息，使用try模块捕获这些错误信息并打印出有用的信息。在ex.csv中没有异常行出现，下载后可以在数据中自行添加空白行测试。
  如果想加载大数据文件，明智的选择通常是使用Numpy的loadtxt()方法，可以很好的处理CSV大数据文件。
  import numpy
  data = numpy.genfromtxt('ex.csv',dtype='str',delimiter='\t')

从Excel文件中导入数据

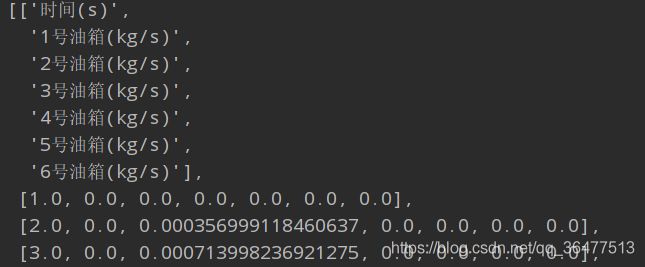
  使用2020年F题附件的excel文件作为示例文件。

import xlrd
import math
filename = '附件2-问题1数据.xlsx'
# 打开工作簿
wb = xlrd.open_workbook(filename = filename)
# 根据名称找到工作表，根据行数(nrows)和列数(ncols)读取单元格的内容
ws = wb.sheet_by_name('油箱供油曲线')
dataset = []
for r in range(ws.nrows):
    col = []
    for c in range(ws.ncols):
        # 添加单元格对象值
        col.append(ws.cell(r,c).value)
    dataset.append(col)
from pprint import pprint
pprint(dataset)

  运行结果：

补充说明：
   print()和pprint()都是python的打印模块，功能基本一样，唯一的区别就是pprint()模块打印出来的数据结构更加完整，每行为一个数据结构，更加方便阅读打印输出结果。特别是对于特别长的数据打印，print()输出结果都在一行，不方便查看，而pprint()采用分行打印输出，所以对于数据结构比较复杂、数据长度较长的数据，适合采用pprint()打印方式。当然，一般情况多数采用print()。

从定宽数据文件导入数据

  对于定宽数据，常见于事件的日志文件和基于时间序列的文件，这些都是数据可视化中最常见的数据源。对于读取，可以逐行读取，然后用字符串操作方法把字符串分割成独立的部分，这种方法比较直接，如果性能不是问题的话可以作为首选。但是当解析的文件非常大时，用python的struct模块能提升性能，因为这个模块是用C语言而不是python编写的。
  这里提供定宽数据源—一百万行的定宽数据，掩码为9s16s6s

import struct
# 指定要读取的数据文件
datafile = 'fixed_width.data'
# 定义数据读取的方式
mask = '9s16s6s'
with open(datafile,'r') as f:
    # 逐行读取文件并根据格式把每行解析成单独的数据字段
    for line in f:
        fields = struct.Struct(mask).unpack_from(str.encode(line))
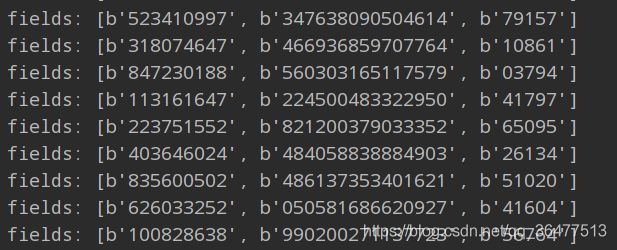
        # 按单独数据字段的形式打印每一行
        print('fields:',[field.strip() for field in fields])

  运行结果：

  工作原理：
    字符串格式是用来定义要提取的数据的期望显示格式，如果掩码定义为9s16s5s，可以读作“9个字符宽度的字符串，跟着一个16字符宽度的字符串，在跟上一个5个字符宽度的字符串”。然后逐行读取文件内容并根据指定的格式解析（通过unpack_from方法）每一行，因为在字段前面（或者后面）可能有多余的空格，用strip()方法可以去掉每个字段的前导和后导空格。

从制表符分隔的文件中读取数据

  另一种常见的平坦数据文件格式是制表符分隔的文件。它可能导出自Excel文件，也可能是一些定制软件的输出。通常我们可以按与CSV文件几乎相同的方式来读取这种格式的文件内容。
  文件可以直接使用上面的CSV文件，只需要将文件后缀名改为tab即可。

import csv
import sys
filename = 'ex.tab'
data = []
try:
    # 打开ex.csv文件
    with open(filename,'rt') as f:
    	# 指定dialect参数为excel_tab语法
        reader = csv.reader(f,dialect=csv.excel_tab)
        # 首先读取文件头
        header = next(reader)
        # 然后读取所有行
        data = [row for row in reader]
except csv.Error as e:
    print('ex.csv文件第{}行出现异常:{}'.format(reader.line_num,e))
    sys.exit(-1)
if header:
    print(header)
    print('=====================')
for datarow in data:
    print(datarow)

  运行结果：

导出数据到Json、CSV和Excel

  使用前面的模块导入、导出和写数据到json、csv和xlsx等各种格式。

# myEncoder.py
import json
class MyEncoder(json.JSONEncoder):

    def default(self, obj):
        """
        只要检查到了是bytes类型的数据就把它转为str类型
        :param obj:
        :return:
        """
        if isinstance(obj, bytes):
            return str(obj, encoding='utf-8')
        return json.JSONEncoder.default(self, obj)

# export.py
# 导入需要的模块
import os
import sys
import argparse
import struct
import json
import csv
try:
    from cStringIO import StringIO
except ImportError:
    from io import StringIO
from io import BytesIO
from myEncoder import MyEncoder
# 定义读写数据
def import_data(import_file):
    # 读取定宽数据
    mask = '9s15s5s'
    data = []
    with open(import_file,'r') as f:
        for line in f:
            fields = struct.Struct(mask).unpack_from(str.encode(line))
            data.append(list([f.strip() for f in fields]))
    return data
def write_data(data,export_format):
    if export_format == 'csv':
        return write_csv(data)
    elif export_format == 'json':
        return write_json(data)
    elif export_format == 'xlsx':
        return write_xlsx(data)
    else:
        raise Exception('Illegal format defined')
# 为每一种数据格式实现方法
def write_csv(data):
    f = StringIO()
    writer = csv.writer(f)
    for row in data:
        writer.writerow(row)
    return f.getvalue()
def write_json(data):
    j = json.dumps(data,cls=MyEncoder,indent=4)
    return j
def write_xlsx(data):
    from xlwt import Workbook
    book = Workbook()
    sheet1 = book.add_sheet('Sheet 1')
    row = 0
    for line in data:
        col = 0
        for datum in line:
            sheet1.write(row,col,str(datum))
            col += 1
        row += 1
        if row > 65535:
            break
    f = StringIO()
    book.save(f)
    return f.getvalue()
if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('import_file',help='Path')
    parser.add_argument('export_format',help='format')
    args = parser.parse_args(['fixed_width.data', 'json'])
    # args = parser.parse_args(['fixed_width.data','csv'])
    # args = parser.parse_args(['fixed_width.data', 'xlsx'])
    if args.import_file is None:
        sys.exit(1)
    if args.export_format not in ('csv','json','xlsx'):
        sys.exit(1)
    if not os.path.isfile(args.import_file):
        sys.exit(1)
    data = import_data(args.import_file)
    print(write_data(data,args.export_format))

  首先，从命令行执行程序，给定两个必选的参数：输入文件名和导出文件格式，成功解析这些参数后，把输入文件分派给import_data()方法。然后，该方法返回列表，就可以方便地对其进行操作并得到合适的输出格式了。

  问题杂谈：
  1)程序报错argparse.PARSER.ArgumentParser of error: the following arguments are required:，是因为需要在parser_args([’…’])写入上面你所预设的参数值，如果输入-h，则返回你的参数和参数说明等帮助提示；
  2)报错TypeError: Object of type bytes is not JSON serializable，dict类型的数据(存在中文)，在python2中是可以转化的，但是在python3中存在序列化问题：TypeError: Object of type bytes is not JSON serializable，解决办法是编写一个解码类 遇到byte就转为str，就是meEncoder，第一步：from myEncoder import MyEncoder；第二步：将json.dumps（data）改写为json.dumps(data,cls=MyEncoder,indent=4)

导入图像数据到Numpy数组

  在科学计算中，图像通常被看作n维数组，图像一般是二维数组，可以被表示为Numpy数组数据结构。因此，对图像执行的一些方法及操作被看作是矩阵操作。

import scipy.misc
import matplotlib.pyplot as plt
# lena = scipy.misc.face()
lena = scipy.misc.ascent()
plt.gray()
plt.imshow(lena)
plt.colorbar()
plt.show()
# 输出点宽和点高
print(lena.shape)
# 整个数组（图像）的最大值
print(lena.max())
# 每个点都被表示为小端整数
print(lena.dtype)

  代码会打开一个新窗口，显示ascent图或者face图的灰度图和坐标轴。颜色条显示了图像上值的范围，在这里显示的是0-黑色到255-白色。
  也可以用PIL读入图像

# 用PIL读入图像
import numpy
from PIL import Image
import matplotlib.pyplot as plt
alg = Image.open('algorithm.jpg')
arr = numpy.array(alg.getdata(),numpy.uint8).reshape(alg.size[1],alg.size[0],3)
plt.gray()
plt.imshow(arr)
plt.colorbar()
plt.show()

  数组切片放大图像
  numpy.memmap做图像内存映射，加快操作图像的速度

生成可控的随机数据集合

  我们常用Python模块生成一些数据集合。然后，就可以用这些数据来了解分布、方差、采样和有些类似的统计学。
  简单介绍几个统计术语：
  分布或者概率分布(Distribution or probability distribution):表示统计实验的结果和发生概率之间的联系
  标准差(Standard deviation)：这个数值表示个体和群体之间的差异。如果差异很大，标准差会比较大；如果个体实验在整组范围内基本相同，标准差会比较小；
  方差(Variance)：标准差的平方
  总体或者统计总体(Population or statistical population)：所有潜在的可观测案例的集合；
  样本(Sample)：总体的子集。
  用Python的random模块生成一个简单的随机数样本

import pylab
import random
SAMPLE_SIZE = 100
# 设置种子
random.seed()
# 生成0-1的随机数
real_rand_vars = [random.random() for val in range(SAMPLE_SIZE)]
# 生成1-6的随机整数
# real_rand_vars = [random.randint(1,6) for val in range(SAMPLE_SIZE)]
# 生成1-6的随机浮点数
# real_rand_vars = [random.uniform(1,6) for val in range(SAMPLE_SIZE)]
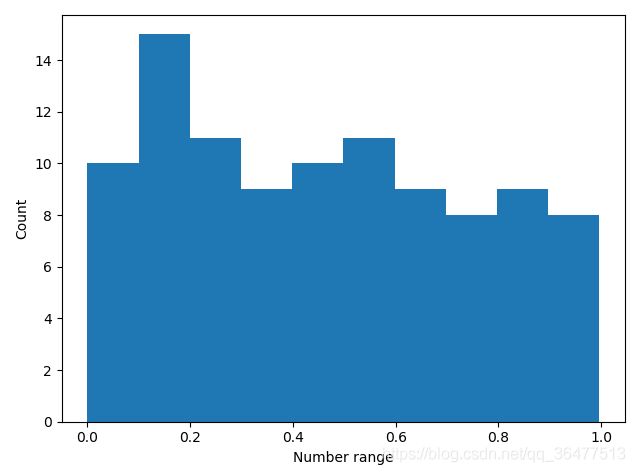
# 创建10个单位的直方图
pylab.hist(real_rand_vars,10)
# 设置x，y轴
pylab.xlabel("Number range")
pylab.ylabel('Count')
pylab.show()

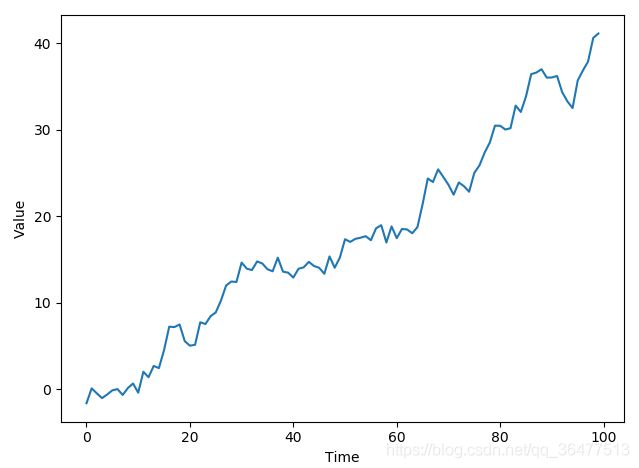
  生成虚拟价格增长数据的时序图，定义了100个数据点，对接下来的每一天，从中值为mean_inc，标准差为std_dev_inc的正态分布中选取一个随机值，然后加上前一天的价格作为当天的价格。

import pylab
import random
# 数据个数
duration = 100
# 中值
mean_inc = 0.2
# 标准差
std_dev_inc = 1.2
x = range(duration)
y = []
price_today = 0
for i in x:
    # 正态分布
    next_delta = random.normalvariate(mean_inc,std_dev_inc)
    price_today += next_delta
    y.append(price_today)
pylab.plot(x,y)
pylab.xlabel('Time')
pylab.ylabel('Value')
pylab.show()

  使用不同的分布

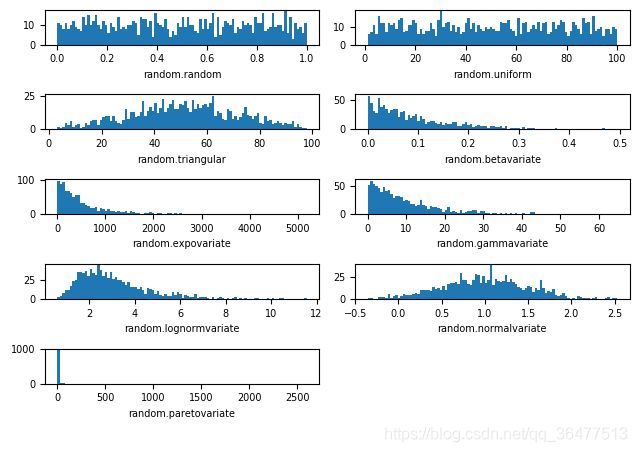
# 创建一个图来容纳并显示所有的直方图
import random
import matplotlib
import matplotlib.pyplot as plt
SAMPLE_SIZE = 1000
buckets = 100
plt.figure()
matplotlib.rcParams.update({'font.size':7})
# 定义6x2的subplot网格来显示所有的直方图
# 1代表行，2代表列，所以一共有2个图，1代表此时绘制第一个图
# 第一个图形是[0,1)之间分布的随机变量
plt.subplot(621)
plt.xlabel('random.random')
res = [random.random() for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 第二个图形是一个均匀分布的随机变量
plt.subplot(622)
plt.xlabel('random.uniform')
res = [random.uniform(1,100) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 三角形分布
plt.subplot(623)
plt.xlabel('random.triangular')
res = [random.triangular(1,100) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 第四个图形是beta分布，参数条件alpha和beta都大于0，返回值在0~1之间
plt.subplot(624)
plt.xlabel('random.betavariate')
res = [random.betavariate(1,10) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 指数分布
plt.subplot(625)
plt.xlabel('random.expovariate')
lambd = 1.0/((SAMPLE_SIZE+1)/2.)
res = [random.expovariate(lambd) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# gamma分布，参数alpha和beta都大于0
plt.subplot(626)
plt.xlabel('random.gammavariate')
res = [random.gammavariate(1,10) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 对数正态分布,如果取这个分布的自然对数，会得到一个中值为mu(任意值)，标准差为sigma(>0)的正态分布
plt.subplot(627)
plt.xlabel('random.lognormvariate')
res = [random.lognormvariate(1,0.5) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 正态分布
plt.subplot(628)
plt.xlabel('random.normalvariate')
res = [random.normalvariate(1,0.5) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
# 帕累托分布，alpha为形状参数
plt.subplot(629)
plt.xlabel('random.paretovariate')
res = [random.paretovariate(1) for _ in range(SAMPLE_SIZE)]
plt.hist(res,buckets)
plt.tight_layout()
plt.show()

补充说明：
  beta分布
  用seed()来初始化伪随机数生成器，这样random()方法就能生成相同的期望随机值。
  如果想避免速记生成的序列重复，推荐使用random.SystemRandom，其底层使用os.urandom，提供了更多的熵源(entropy source)的访问，使用这个随机数生成器接口，seed()和setstate()没有影响，样本就不是可重现的了。

真实数据的噪声平滑处理

  来自各种真实世界传感器的数据通常是不平滑和不干净的，包含了一些我们不想显示在图标或者图形中的噪声。基础算法是基于滚动窗口(rolling window)模式(例如卷积).。窗口滚动当过数据，然后计算出窗口内数据的平均值。对于离散数据，使用Numpy的canvolve方法，它返回两个一维序列的离散线性卷积。使用Numpy的linspace方法，它生成一个给定间隔的等距数字序列。方法ones定义了一个所有元素值为1的序列或者矩阵(例如多维数组),可以用它来生成用于求平均值的窗口。
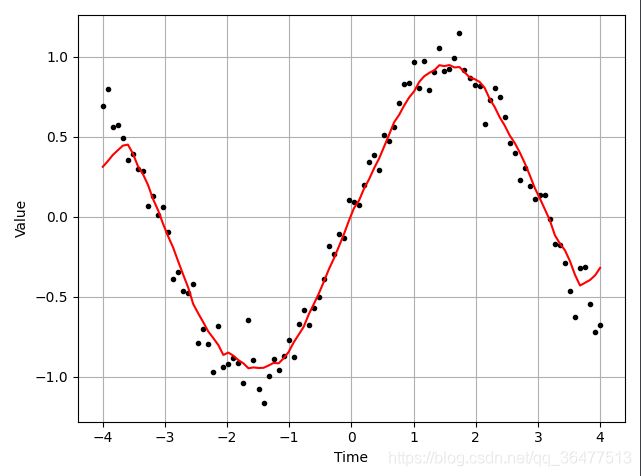
  平滑数据噪声的一个简单做法就是，对窗口(样本)求平均，然后仅仅绘制出给定窗口的平均值，而不是所有的数据点，这也是更高级算法的基础。

import matplotlib.pyplot as plt
from numpy import *
def moving_average(interval,window_size):
    window = ones(int(window_size))/float(window_size)
    return convolve(interval,window,'same')
t = linspace(-4,4,100)
y = sin(t) + random.randn(len(t)) * 0.1
plt.plot(t,y,'k.')
y_av = moving_average(y,10)
plt.plot(t,y_av,'r')
plt.xlabel('Time')
plt.ylabel('Value')
plt.grid(True)
plt.show()

  可以看出平滑处理后的曲线和原始数据点之间的对比情况。

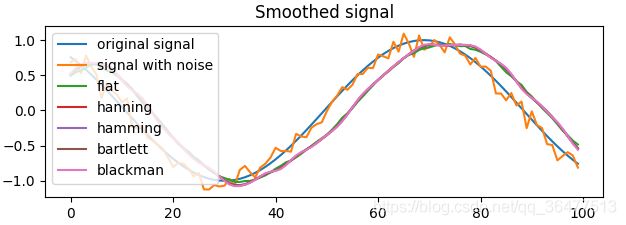
  使用现有的Scipy库来让窗口处理达到更好的效果。基于信号(指数据点)窗口的卷积(函数的总和)。向两端添加相同信号的副本并做反射，这样一来，就减小了数据的边界效应。

import numpy
from numpy import *
import matplotlib.pyplot as plt

# 如果你只想看到两个窗口类型，注释前一行，取消注释后一行
WINDOWS = ['flat', 'hanning', 'hamming', 'bartlett', 'blackman']


# WINDOWS = ['flat','hanning']


def smooth(x, window_len=11, window='hanning'):
    """
    使用要求大小的窗口平滑数据
    :param x: 输入信号
    :param window_len: 平滑窗口的长度
    :param window: 窗口类型('flat','hanning','hamming','bartlett','blackman')
    :return: 平滑信号
    平窗将产生一个移动平均平滑
    """
    if x.ndim != 1:
        raise ValueError('函数只接受一维数组')
    if x.size < window_len:
        raise ValueError('输入向量需要大于窗口大小')
    if window_len < 3:
        return x
    if window not in WINDOWS:
        raise ValueError('window应为\'flat\',\'hanning\',\'hamming\',\'bartlett\',\'blackman\'中的一个')
    # 在前面和后面增加反射窗口
    s = numpy.r_[x[window_len - 1:0:-1], x]
    # 选择窗口类型并做平均
    if window == 'flat':  # 移动平均
        w = numpy.ones(window_len, 'd')
    else:
        # 在numpy中调用函数
        w = eval('numpy.' + window + '(window_len)')
    # 注意: length(output) != length(input)，更正如下:  # return y[(window_len/2-1):-(window_len/2)]替代y。
    y = numpy.convolve(w / w.sum(), s, mode='valid')
    return y


# 在指定的时间间隔内获得一些均匀间隔的数字。
t = linspace(-4, 4, 100)
# 制造有噪声的正弦曲线
x = sin(t)
xn = x + random.randn(len(t)) * 0.1
y = smooth(x)
ws = 31
plt.subplot(211)
plt.plot(ones(ws))
# 每一个窗口
for w in WINDOWS[1:]:
    eval('plot(' + w + '(ws)')
# 配置轴属性
plt.axis([0,30,0,1.1])
# 为每个窗口添加图例
plt.legend(WINDOWS)
plt.title('Smoothing windows')
# 添加第二个图
plt.subplot(212)
# 原始信号
plt.plot(x)
# 添加噪声
plt.plot(xn)
# 平滑信号与噪声为每一个可能的窗口算法
for w in WINDOWS:
    plt.plot(smooth(xn,10,w))
# 为每一个图添加图例
l = ['original signal','signal with noise']
l.extend(WINDOWS)
plt.legend(l)
plt.title('Smoothed signal')
plt.show()

巨量数据使用与保存——pickle(泡菜，可理解为永久保存)

import pickle
f1 = open('test.pkl','wb')
list1 = [1,'python',[1,2].{1:2}]
# 把对象序列化，扔进泡菜坛
pickle.dump(list1,f)
f1.close()
f2 = open('test.pkl','rb')
# 数据流进行反序列化
list2 = pickle.load(f2)