Save Money for Your Company 最小矩形覆盖（非计算几何）/找出N条直线相交点的边缘点/ find the dominating points of N lines

Save Money for Your Company!

Description

You are the director of a mining enterprise, aiming to purchase an mining land for your company. This land has already been criss-crossed with a lot of mining tunnels. In the trading, the vendor demand to restrict the area of purchased land by a rectangle, and the direction of the width of this rectangular is fixed. For the smooth running of mining activities, you have to make this area contains all the intersections of mining tunnels, otherwise the ore may enter the unauthorized (unpurchased) area in the process of transportation or exploitation. Now there is question for you: what is the minimum area of this rectangle? This makes sense because you have to save the cost of purchasing land by shrinking the rectangular area as much as possible.

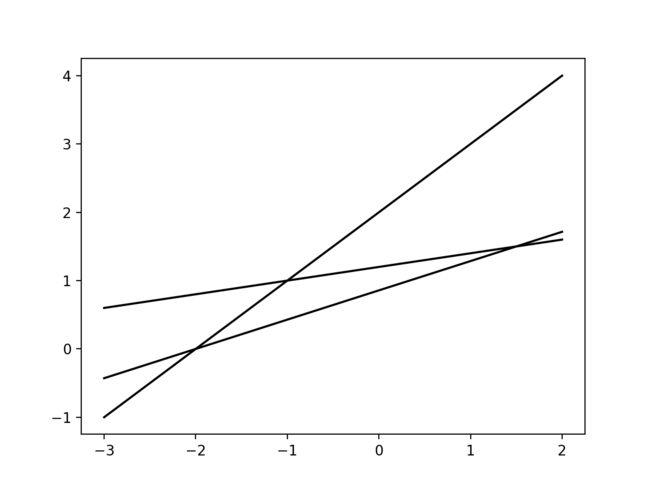
One can introduce coordinate system into this. Let the x,y coordinate axis parallel to the width and height of this rectangle, and use straight lines to represent mining tunnels. For example:

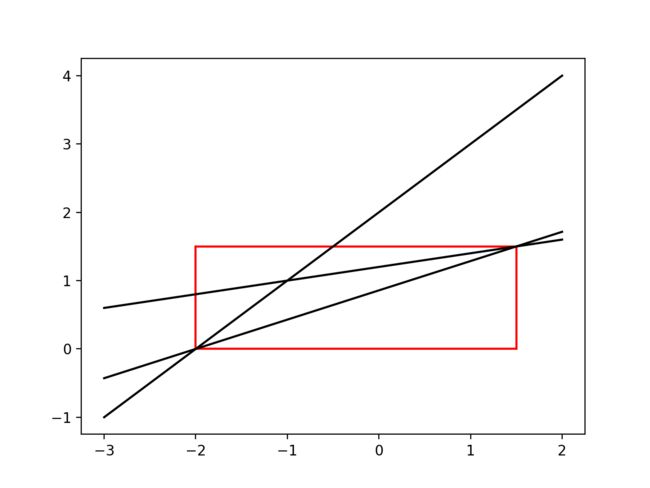
There are 3 tunnels and 3 intersections. Find a minimum rectangle to contain all the intersections (Notice that the width and height are parallel to the axis):

This is the answer.

In this question, you have to work out an algorithm to calculate the minimum area of rectangle stated above, given the (a,b) pairs of the coefficients in the equations (y=ax+b) representing mining tunnels. If no such rectangle exists, return 0. Your answer is true if relative error or absolute error is smaller than 10^(-4).

Notice that, in this question, a > 0, and a, b are integers.

Sample Input 1

Lines of strings, and each line is the string form of 2 numbers [a,b] (split by space)

Copy

2 3
1 2
3 4

Sample Output 1

A floating point number.

 0.00000

Explanation of Sample 1

3 straight lines: y=2x+3,y=x+2,y=3x+4. These 3 lines intersect at the same point: (-1, 1). Therefore, the rectangle does not exist.

Sample Input 2

Lines of strings, and each line is the string form of 2 numbers [a,b] (split by space)

4 1
2 3
3 0

Sample Output 2

A floating point number.

 48.00000

Explanation of Sample 2

3 straight lines: y=4x+1,y=2x+3,y=3x. These 3 lines intersect at the 3 points: (3, 9)(-1, -3)(1, 5). Therefore, the rectangle formed by (3, 9)(-1, -3) is the smallest, and the area is 48.00000.

Constraints of 10 test cases

Case 1: 1

Case 2-4: 100

Case 5-7: 1000

Case 8-10: 10000

#include
#include
#include
#include
#include
#include
using namespace std;
struct node{
    long double x,y;
};
node vex[100005];

bool cmp1(node a,node b){
    return a.x