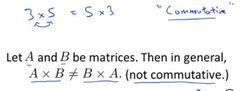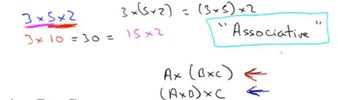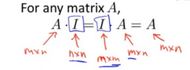Linear Algebra review - Matrix multiplication properties
摘要: 本文是吴恩达 (Andrew Ng)老师《机器学习》课程,第三章《线性代数回顾》中第18课时《矩阵乘法特征》的视频原文字幕。为本人在视频学习过程中记录下来并加以修正,使其更加简洁,方便阅读,以便日后查阅使用。现分享给大家。如有错误,欢迎大家批评指正,在此表示诚挚地感谢!同时希望对大家的学习能有所帮助。
Matrix multiplication is really useful since you can pack a lot of computation into just one matrix multiplication operation. But you should be careful of how you use them. In this video (article), I want to tell you about a few properties of matrix multiplication.
Matrix multiplication is not commutative
When working with just real numbers, or when working with scalars, multiplication is commutative. And what I mean by that is if you take ![]() , that is equal to
, that is equal to ![]() , and the ordering of this multiplication doesn't matter. And this is called the commutative property of multiplication of real numbers. It turns out this property is not true for matrix multiplication. Concretely, if
, and the ordering of this multiplication doesn't matter. And this is called the commutative property of multiplication of real numbers. It turns out this property is not true for matrix multiplication. Concretely, if ![]() and
and ![]() are matrices,
are matrices, ![]() is not equal to
is not equal to ![]() . Just be careful of that. It is not okay to arbitrarily reverse the order in which you were multiplying matrices. So, we say the matrix multiplication is not commutative, it's a fancy way of saying it.
. Just be careful of that. It is not okay to arbitrarily reverse the order in which you were multiplying matrices. So, we say the matrix multiplication is not commutative, it's a fancy way of saying it.
As a concrete example, ![]() . Now, let's swap around the order of these two matrices. It turns out if you multiply these two matrices, you get
. Now, let's swap around the order of these two matrices. It turns out if you multiply these two matrices, you get ![]() . Clearly, these two results are not equal to each other.
. Clearly, these two results are not equal to each other.
So, in fact, in general, if you have a matrix operation, like ![]() . If
. If ![]() is
is ![]() matrix, and
matrix, and ![]() is
is ![]() matrix. Then it turns out that
matrix. Then it turns out that ![]() is going to be an
is going to be an ![]() matrix, whereas
matrix, whereas ![]() is going to be
is going to be ![]() matrix, so the dimension even doesn't match.
matrix, so the dimension even doesn't match.
Matrix multiplication is associative
When talking about real numbers, or scalars, let's say, I have ![]() . I can either compute this as
. I can either compute this as ![]() . Or I can compute
. Or I can compute ![]() . And both of these give you the same answer. This is called the associative property of real number multiplication. It turns out that matrix multiplication is associative. So concretely, let's say I have a product of three matrices,
. And both of these give you the same answer. This is called the associative property of real number multiplication. It turns out that matrix multiplication is associative. So concretely, let's say I have a product of three matrices, ![]() . Then I can compute this either as
. Then I can compute this either as ![]() , or I can compute this as
, or I can compute this as ![]() , and these will actually give me the same answer.
, and these will actually give me the same answer.
So just be clear what I mean by these two cases. Let's look at the first case. What I mean by that is if you actually want to compute ![]() , you can first compute
, you can first compute ![]() . So that
. So that ![]() , then compute
, then compute ![]() . Or for this second case, you can set
. Or for this second case, you can set ![]() , then compute
, then compute ![]() . And it turns out that both of these two options will give you, is guaranteed to give you the same answer. And so, we say that matrix multiplication is does enjoy the associative property.
. And it turns out that both of these two options will give you, is guaranteed to give you the same answer. And so, we say that matrix multiplication is does enjoy the associative property.
Identity matrix
Finally, I want to tell you about the identity matrix which is special matrix. When dealing with real numbers or scalar numbers, the number ![]() , is you can think of it as the identity of multiplication, and what I mean by that is that for any number
, is you can think of it as the identity of multiplication, and what I mean by that is that for any number ![]() ,
, ![]() . So
. So ![]() is the identity operation and so it satisfies this equation. So, it turns out that in the space of matrices, there's an identity matrix as well. And it's usually denoted
is the identity operation and so it satisfies this equation. So, it turns out that in the space of matrices, there's an identity matrix as well. And it's usually denoted ![]() , or sometimes we write it as
, or sometimes we write it as ![]() . We want to make explicit the dimensions.
. We want to make explicit the dimensions.
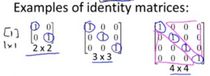
And so, there's a different identity matrix for each dimension ![]() , and here are a few examples. Here's the
, and here are a few examples. Here's the ![]() identity matrix. Here's the
identity matrix. Here's the ![]() identity matrix. Here's the
identity matrix. Here's the ![]() identity matrix. So, the identity matrix has the property that it has ones along the diagonals, and is zero everywhere else. And by the way, the
identity matrix. So, the identity matrix has the property that it has ones along the diagonals, and is zero everywhere else. And by the way, the ![]() identity matrix is just a number one (
identity matrix is just a number one (![]() ).
).
And informally when I or others are being sloppy very often, we'll write the identity matrix using fine notation. Just write 1111, dot, dot, dot, 1 and then we'll, maybe, somewhat sloppily write a bunch of zeros there.
It turns out that identity matrix has this property that for any matrix ![]() ,
, ![]() . So that's a lot like this equation (
. So that's a lot like this equation (![]() ) that we have up here. Just make sure we have the dimensions right. So, for
) that we have up here. Just make sure we have the dimensions right. So, for ![]() , if
, if ![]() is
is ![]() matrix, then this identity matrix is an
matrix, then this identity matrix is an ![]() identity matrix. And for
identity matrix. And for ![]() , if
, if ![]() is
is ![]() , this identity matrix is an
, this identity matrix is an ![]() matrix. In either case, the outcome of this process is you get back to matrix
matrix. In either case, the outcome of this process is you get back to matrix ![]() which is
which is ![]() . So, whenever you write the identity matrix
. So, whenever you write the identity matrix ![]() , the dimension will be implicit in the context. So these two
, the dimension will be implicit in the context. So these two ![]() , they're actually different dimension matrices, one is
, they're actually different dimension matrices, one is ![]() , the other is
, the other is ![]() . But when we want to make the dimension of the matrix explicit, then sometimes we'll write to this
. But when we want to make the dimension of the matrix explicit, then sometimes we'll write to this ![]() . But very often the dimension will be implicit.
. But very often the dimension will be implicit.
Finally, just want to point out that, earlier I said that, in general, ![]() , right? That for most matrices
, right? That for most matrices ![]() and
and ![]() , this is not true. But when
, this is not true. But when ![]() is the identity matrix, this does hold true. That
is the identity matrix, this does hold true. That ![]() . This is not true for other matrices
. This is not true for other matrices ![]() in general.
in general.
So that's it for the properties of matrix multiplication. And the special matrices, like the identity matrix. In the next and final video (article) in our linear algebra review, I'm going to quickly tell you about a couple of special matrix operations, and after that you know everything you need to know about linear algebra for this course.