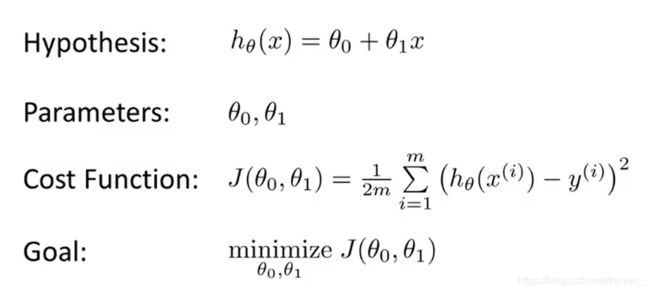【吴恩达机器学习笔记】1引言、单变量线性回归、线性代数回顾
1引言(Introduction)
1.1欢迎(Welcome)
1.2机器学习是什么(What is machine learning?)
- Arthur Samuel(1959):机器学习是在没有进行特定编程的情况下,给予计算机学习能力的领域。
- Tom Mitchell(1998):一个好的学习问题定义如下,一个程序被认为能从经验E中学习,解决任务T,达到性能度量值P,当且仅当有了经验E后,经过P评判,程序在处理T时的性能有所提升。
机器学习算法包括监督学习(Supervised learning)、非监督学习(Unsupervised learning)、强化学习(Reinforcement learning)、推荐系统(Recommender systems)等。
1.3监督学习(Supervised learning)
监督学习指给学习算法一个数据集,这个数据集由“正确答案”组成,再根据数据集样本作出预测。
回归(Regression)指试着推测出这一系列连续值属性。
分类(Classfication)指试着推测出离散的输出值。
1.4非监督学习(Unsupervised learning)
无监督学习中没有任何的标签或者是有相同的标签。针对数据集,无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做聚类算法(Clustering algorithm)。
聚类的应用:组织大型计算机集群、社交网络分析、市场分割、天文数据分析等。
鸡尾酒会问题(Cocktail party problem):从音频中分离出音频,解决代码:[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');
2单变量线性回归(Linear Regression with One Variable)
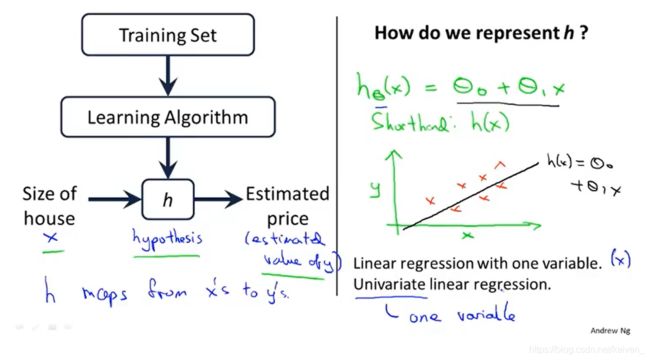
2.1模型表示(Model representation)
回归问题的标记如下:
m m m:训练集中实例的数量
x x x:特征/输入变量
y y y:目标变量/输出变量
( x , y ) \left( x,y \right) (x,y):训练集中的实例
( x ( i ) , y ( i ) ) ({{x}^{(i)}},{{y}^{(i)}}) (x(i),y(i)):第 i i i个观察实例
h h h:学习算法的解决方案或函数也称为假设(hypothesis)
2.2代价函数(Cost function)
模型所预测的值与训练集中实际值之间的差距是建模误差(modeling error)。我们的目标是选择出使得建模误差的平方和能够最小的模型参数。 即使得代价函数最小 m i n J ( θ 0 , θ 1 ) min\space J(\theta_0,\theta_1) min J(θ0,θ1)。代价函数也被称作平方误差函数或平方误差代价函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
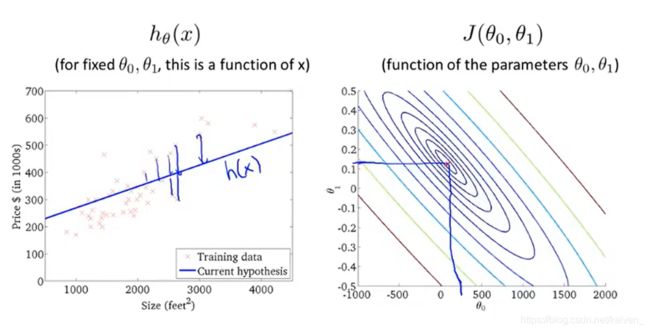
2.3/2.4代价函数的直观理解(Cost function intuition)
2.5梯度下降(Gradient descent)
梯度下降是一个用来求函数最小值的算法,使用梯度下降算法来求出代价函数 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1) 的最小值。
梯度下降思想是:开始时随机选择一个参数的组合 ( θ 0 , θ 1 , . . . . . . , θ n ) \left( {\theta_{0}},{\theta_{1}},......,{\theta_{n}} \right) (θ0,θ1,......,θn)计算代价函数,然后寻找下一个能让代价函数值下降最多的参数组合。持续直到找到一个局部最小值(local minimum),因为并没有尝试完所有的参数组合,所以不能确定得到的局部最小值是否是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
批量梯度下降(batch gradient descent)算法公式: θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) θj:=θj−α∂θj∂J(θ0,θ1)
α \alpha α是学习率(learning rate),它决定沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

2.6梯度下降直观理解(Gradient descent intution)
在梯度下降法中,当接近局部最低点时(导数为0),梯度下降法会自动采取更小的幅度,这是因为当接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度。所以实际上没有必要再另外减小 α \alpha α。
2.7梯度下降的线性回归(Gradient descent for linear regression)
对之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即: ∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial }{\partial {{\theta }_{j}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{\partial }{\partial {{\theta }_{j}}}\frac{1}{2m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}^{2}} ∂θj∂J(θ0,θ1)=∂θj∂2m1i=1∑m(hθ(x(i))−y(i))2
j = 0 j=0 j=0 时: ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial {{\theta }_{0}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}} ∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
j = 1 j=1 j=1 时: ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) \frac{\partial }{\partial {{\theta }_{1}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)} ∂θ1∂J(θ0,θ1)=m1i=1∑m((hθ(x(i))−y(i))⋅x(i))
则算法改写成:
Repeat {
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) {\theta_{0}}:={\theta_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{ \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)} θ0:=θ0−am1i=1∑m(hθ(x(i))−y(i))
θ 1 : = θ 1 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) {\theta_{1}}:={\theta_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)} θ1:=θ1−am1i=1∑m((hθ(x(i))−y(i))⋅x(i))
}
3线性代数回顾(Linear Algebra review)
3.1矩阵和向量(Matrices and vectors)
3.2加法和标量乘法(Addition and scalar multiplication)
3.3矩阵向量乘法(Matrix-vector multiplication)
3.4矩阵乘法(Matrix-matrix multiplication)
3.5矩阵乘法的性质(Matrix multiplication properties)
不满足交换律: A × B ≠ B × A A×B≠B×A A×B=B×A
满足结合律: A × ( B × C ) = ( A × B ) × C A×(B×C)=(A×B)×C A×(B×C)=(A×B)×C
A A − 1 = A − 1 A = I A{{A}^{-1}}={{A}^{-1}}A=I AA−1=A−1A=I
对于单位矩阵有: A I = I A = A AI=IA=A AI=IA=A
3.6逆、转置(Inverse and transpose)
( A ± B ) T = A T ± B T {{\left( A\pm B \right)}^{T}}={{A}^{T}}\pm {{B}^{T}} (A±B)T=AT±BT ( A × B ) T = B T × A T {{\left( A\times B \right)}^{T}}={{B}^{T}}\times {{A}^{T}} (A×B)T=BT×AT ( A T ) T = A {{\left( {{A}^{T}} \right)}^{T}}=A (AT)T=A ( K A ) T = K A T {{\left( KA \right)}^{T}}=K{{A}^{T}} (KA)T=KAT