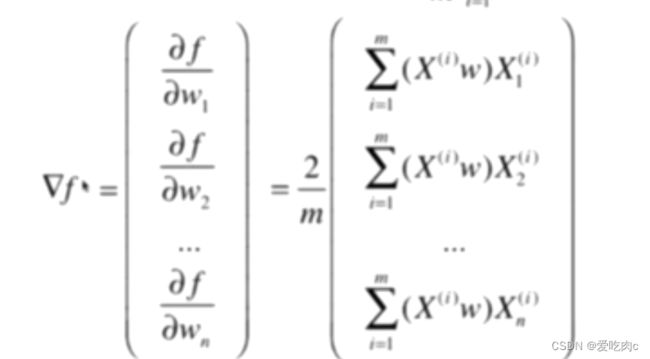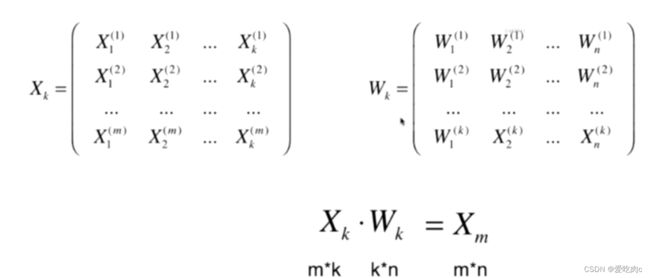机器学习--PCA主成分分析
文章目录
- 一、PCA(principal component analysis)
-
- 1、概述
- 2、主要作用:降维
- 3、主成分分析与线性回归要区分
-
- 1、主成分分析
- 2、线性回归
- 二、使用梯度上升法解决PCA问题
-
- 1、公式推导:
- 2、 代码实现求一个主成分
- 3、求取数据的前n个主成分
-
- 1、代码实现
- 三、高维数据向低维数据的映射
- 四、封装属于自己的pca
- 五、sklearn中的PCA
-
- 1、简单应用
- 2、PCA中的其他方法(用一个真实数据来测试)
- 五、总结:
一、PCA(principal component analysis)
1、概述
2、主要作用:降维
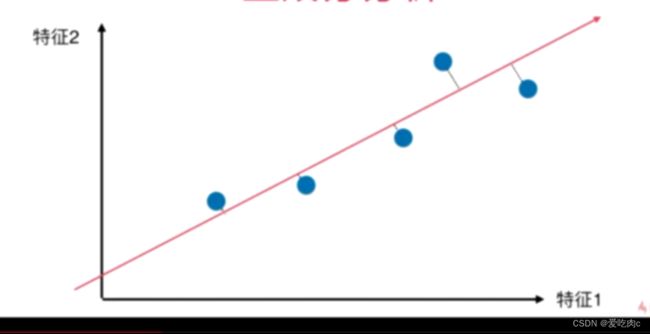
简单的变成一维:我们可以选择一个特征,把另一个特征舍弃,如下图:
相对而言,右侧比左侧好,更有区分度,但它显然不是最好的方案
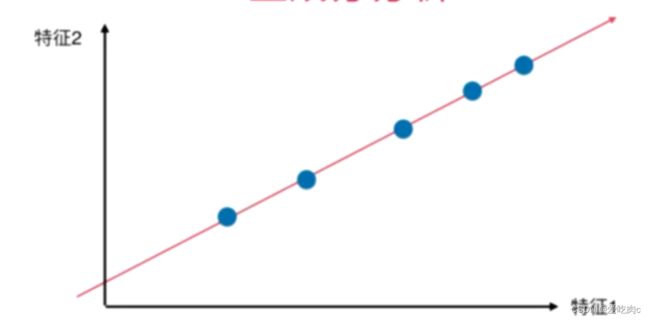
如果我们把所有数据都映射在红色这条直线上,显然比上述两个方案好,这个分布与原始分布更接近
显然,我们想要找到使样本映射在轴上时,样本间间距可以最大,更有区分度
在这里我们可以使用方差这个概念,方差越大即点越系数,即样本间间距也就越大

为了找到方差最大的轴,我们第一步需要先将样本的均值归0(demean)
为什么要demean 下述即可看到。均值归零很简单,像我之前写的文章的均值方差归一化一样,每个样本值减去均值即可。

注意,这里我们就可以知道为什么要demean操作,使计算更简单。
同时要注意这里的Xi是样本已经映射在红色这条轴之后的坐标,而不是原始坐标
因为是为了求样本点映射在一个轴上之后的样本间距最大。
在这里 我们是对二维降维成一维,所以w是一个二维方向向量,表示我们最终要映射的轴的方向

虽然样本X映射在w这个轴上,是一维的,但此时w和X仍然是在二维平面中,是一个二维向量
并且通过降维 X映射后的平均值应该为(0,0),此时方差变为

如何求X映射在w上的长度 ? 利用向量点积 w是一个方向向量 大小为1


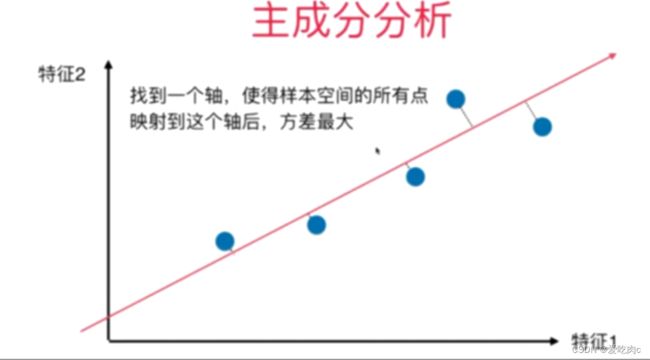
3、主成分分析与线性回归要区分
1、主成分分析
主成分分析是找到一个轴使样本间距最大
样本是垂直映射到该轴上的
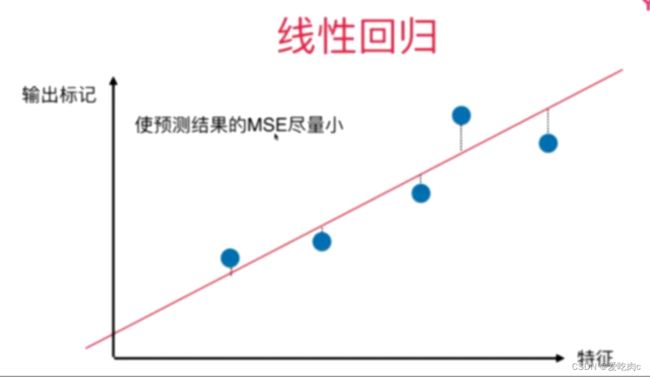
2、线性回归
线性回归是找到一条线性回归方程,使对于样本中的x在该方程上的值(预测值)与真实值最为接近。
样本x是垂直于x映射在该回归方程的直线上
二、使用梯度上升法解决PCA问题
1、公式推导:
使用梯度法肯定要先求梯度 X是一个矩阵 m行n列 m个样本 n个特征
其实到这里就可以使用for循环编程了,但是我们可以利用向量化 使其更简单 X*W 就是一个向量
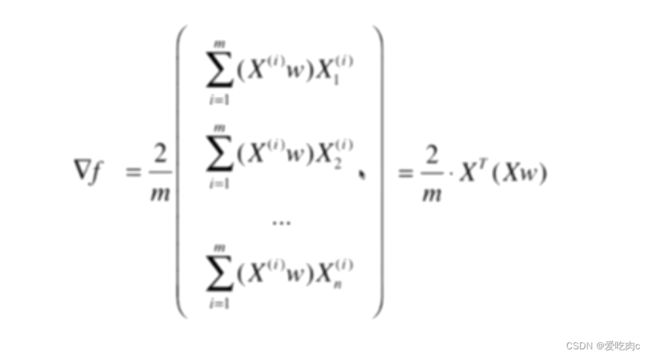
梯度是一个m行1列的向量 但通过化简后求得的使 1行m列 所以我们需要在进行一次转置
即最终梯度为:
2、 代码实现求一个主成分
f(x)上文中有显示求法 即方差
dj_math 是我们推导出来的梯度
dj_debug 是高数中的导数求法 如上篇文章中 这个函数可以来计算我们的梯度计算是否准确
注意:这里的数据不能使用均值方差归一化,因为我们求得就是方差的最大值
若均值方差归一化 那方差就固定为1 没有意义
同时,这里的w是一个方向向量,且模为1 ,与上文公式一致
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.,100.,size=100)
x[:,1]=0.75*x[:,0]+3.+np.random.normal(0,10,size=100)
def demean(x):
return x-np.mean(x,axis=0)
demean_x=demean(x)
def f(x,w):
return np.sum((x.dot(w)**2.))/len(x)
def dj_math(x,w):
return x.T.dot(x.dot(w))*2./len(x)
def dj_debug(x,w,epsilon=0.001):
res=np.empty(len(w))
w_1=w.copy()
w_1+=epsilon
w_2=w.copy()
w_2-=epsilon
res=(f(x,w_1)-f(x,w_2))/(2*epsilon)
return res
def direction(w): #我们在公式推导中使用的是方向向量 所以需要让w的模为1
return w/np.linalg.norm(w)
def gradient_ascend(dj,x,initial_w,eta,n_iters=1e3,epsilon=1e-8):
w=direction(initial_w)
cur_iter=0
while cur_iter<n_iters:
gradient=dj(x,w)
last_w=w
w=w+eta*gradient
w=direction(w)
if(abs(f(x,w)-f(x,last_w))<epsilon):
break
cur_iter+=1
return w
initial_w=np.random.random(x.shape[1]) #注意这里初始w不能为0,因为0也是一个极值点 但是是极小值点,我们要求得是极大值点
eta=0.01
w=gradient_ascend(dj_math,demean_x,initial_w,eta)
plt.scatter(demean_x[:,0],demean_x[:,1])
plt.plot([0,w[0]*50],[0,w[1]*50],color='r')
plt.show()
3、求取数据的前n个主成分
主成分分析是为 了降维,如数据中变量太多,会导致问题复杂,主成分分析可以去除数据中一些不必要的噪音一些不必要的数据,使得问题简单化。但是对于有多个变量的数据,我们不能只求取一个主成分,因为一个主成分的信息可能不能够准确的表示数据。
此时,我们就要求取多个主成分
但是,第一主成分包含的数据信息一定是最多的,即方差最大的,第二主成分次之…
如何求取数据的前n个主成分呢?
如前一个代码,我们求取了第一个主成分,之后我们如果要求取第二个主成分
一定是要用原先数据减去第一个主成分的信息。
1、代码实现
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.,100.,size=100)
x[:,1]=0.75*x[:,0]+3.+np.random.normal(0,10,size=100)
def demean(x):
return x-np.mean(x,axis=0)
demean_x=demean(x)
def f(x,w):
return np.sum((x.dot(w)**2.))/len(x)
def dj(x,w):
return x.T.dot(x.dot(w))*2./len(x)
def direction(w): #我们在公式推导中使用的是方向向量 所以需要让w的模为1
return w/np.linalg.norm(w)
def first_component(x,initial_w,eta,n_iters=1e3,epsilon=1e-8):
w=direction(initial_w)
cur_iter=0
while cur_iter<n_iters:
gradient=dj(x,w)
last_w=w
w=w+eta*gradient
w=direction(w)
if(abs(f(x,w)-f(x,last_w))<epsilon):
break
cur_iter+=1
return w
#求前n个主成分
def first_n_component(n,x,eta=0.01,n_iters=1e3,epsilon=1e8):
x_1=x.copy()
x_1=demean(x_1) #将平均值变为0
res=[]
for i in range(n):
initial_w=np.random.random(x.shape[1]) #注意这里初始w不能为0,因为0也是一个极值点 但是是极小值点,我们要求得是极大值点
w=first_component(x_1,initial_w,eta)
res.append(w)
x_1=x_1-x_1.dot(w).reshape(-1,1)*w #x_1.dot(w) 即x在w上的映射长度 在*w这个方向就变成一个向量
return res
first_n_component(2,x) #因为x是二维的只能求2个主成分 在这里我们求取前2个主成分
#且前两个主成分是垂直的
三、高维数据向低维数据的映射
上述中,我们虽然求取了前n个主成分,但是并没有降维,对于样本中的数据,仍然是m行n列
例如:如果我们求取了前k个主成分,前k个主成分已经可以表示该数据的主要信息了

我们如何将我们的样本从n维转换为k维呢??
让X的第一行乘以Wk的第一行即X中的第一个数据在这k维中的映射,点乘
以此类推 即把X从n维变为了k维,实现了降维的过程。
同样,我们也可以把降维的数据恢复成高维,但此时恢复的高维数据已经改变了,因为我们在变为低维的同时已经丢失了一些数据
四、封装属于自己的pca
# 时间:2022/11/19 17:47
# cky
import numpy as np
class PCA:
def __init__(self,n_component):
#n_component 是想要变成几维
self.n_component=n_component
#component 是我们根据用户传来的数据 求得的主成分
self.component_=None
#fit操作 即求取前n个主成分
def fit(self,x,eta=0.01,n_iters=1e4):
def demean(x):
return x - np.mean(x, axis=0)
#求函数
def f(x, w):
return np.sum((x.dot(w) ** 2.)) / len(x)
#求梯度
def dj(x, w):
return x.T.dot(x.dot(w)) * 2. / len(x)
#变为单位向量
def direction(w): # 我们在公式推导中使用的是方向向量 所以需要让w的模为1
return w / np.linalg.norm(w)
#求主成分
def first_component(x, initial_w, eta, n_iters=1e3, epsilon=1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
gradient = dj(x, w)
last_w = w
w = w + eta * gradient
w = direction(w)
if (abs(f(x, w) - f(x, last_w)) < epsilon):
break
cur_iter += 1
return w
demean_x = demean(x)
self.component_=np.empty(shape=(self.n_component,x.shape[1]))
for i in range(self.n_component):
initial_w=np.random.random(x.shape[1])
w=first_component(demean_x,initial_w,eta,n_iters)
self.component_[i,:]=w
demean_x=x-x.dot(w).reshape(-1,1)*w
return self
#将高维变低维
def transform(self,x):
return x.dot(self.component_.T)
#将低维恢复成高维
def restore(self,x):
return x.dot(self.component_)
五、sklearn中的PCA
1、简单应用
from sklearn.decomposition import PCA
pca=PCA(n_components=1)
pca.fit(x)
pca.transform(x).shape
2、PCA中的其他方法(用一个真实数据来测试)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits=datasets.load_digits()
x=digits.data
y=digits.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y)
from sklearn.neighbors import KNeighborsClassifier
#用全部数据集来测试一下识别率
%time knn=KNeighborsClassifier()
knn.fit(x_train,y_train)
knn.score(x_test,y_test)
Wall time: 1.17 ms
0.9888888888888889
#通过降维来测试一下识别率
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca.fit(x)
x_train_reduction=pca.transform(x_train)
x_test_reduction=pca.transform(x_test)
%time knn=KNeighborsClassifier()
knn.fit(x_train_reduction,y_train)
knn.score(x_test_reduction,y_test)
Wall time: 0 ns
0.62
#可以看出从64到2维 识别率下降了太多,我们如何找到适合的识别率呢?
pca.explained_variance_ratio_ #这个函数可以帮助我们看每个主成分可以解释数据的多少
#可以看出 前两个成分一共才解释了大约百分之28 太少
pca=PCA(n_components=64) #该数据共64维 我们先把所有都求出来
pca.fit(x_train)
pca.explained_variance_ratio_ #看每个主成分都解释多少
plt.plot([i for i in range(x_train.shape[1])],[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(x_train.shape[1])])
plt.show() #绘制出来
#pca也为我们提供了另一个方法,在实例化pca时,我们不传入要求多少个主成分
#我们传入一个0-1的数,表示我们想要表示原始数据的多少成分
pca=PCA(0.95)
pca.fit(x_train)
x_train_reduction=pca.transform(x_train)
x_test_reduction=pca.transform(x_test)
%time knn=KNeighborsClassifier()
knn.fit(x_train_reduction,y_train)
knn.score(x_test_reduction,y_test)
pca.n_components_
Wall time: 0 ns
0.98
28
通过以上代码
我们可以发现把一个64维数据降到28维后即可保持原始数据百分之95的成分
并且 通过降维 运算时间也提升了许多
五、总结:
今天得内容感觉有点多,自己也需要慢慢消化。一起加油吧
记住:慢就是快。在这个浮躁的社会中,自己静下心来学习真的很棒了!