经典进程同步问题
1. 生产者消费者问题
问题描述
存在若干生产者进程、若干消费者进程和由n个缓冲区组成的缓冲池。现规定最初缓冲池中没有数据,生产者需要在缓冲池未满的情况下向缓冲池写入数据,消费者需要在缓冲池未空的情况下从缓冲池读取数据。
过程如图:
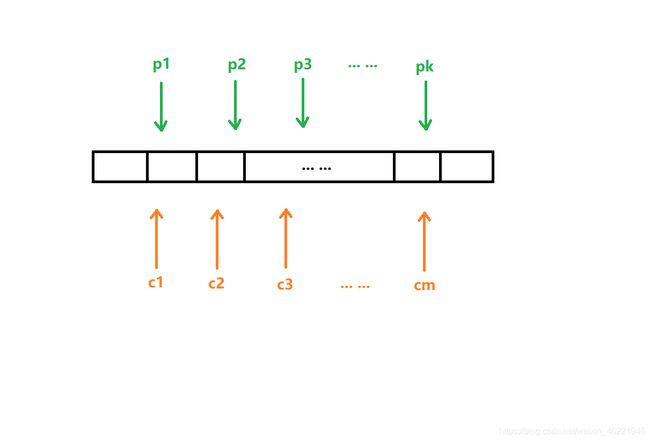
可以将缓冲池视为循环队列,在循环队列的头部实现对缓冲池的写入,在循环队列的尾部实现对缓冲池的读取。
分析
显然,多个p进程(producer)之间为互斥关系,因为假如现在队头指针in指向第3个缓冲区,若存在多个p进程对第3个缓冲区进行写操作,会发生冲突。同样的,对于c程序(consumer)也是类似的,因此缓冲池为临界资源。综上可得,所有进程之间均为互斥关系。但是对于全部p进程与全部c进程而言,也存在着同步的关系,即生产之后方可消费。
因为所有进程互斥,因此设置一个mutex以控制一个进程访问缓冲池;设置empty信号,其实是对于空余缓冲区个数的统计,而full信号是对已填充缓冲区个数的统计,即二者的关系为n = empty + full,这是控制同步的信号量。
代码
Semaphore mutex = 1, empty = n, full = 0;
int in = 0, out = 0;
item Buffer[n];
void Producer() {
do{
Produce_an_Item_NextP; //计算一个数据
P(empty);
P(mutex);
Buffer[in] = NextP; //临界区
in = (in+1) % n;
V(mutex);
V(full);
} while(TRUE)
}
void Consumer()
{
do {
P(full);
P(mutex);
NextC = Buffer[out]; // 临界区
out = (out+1) % n;
V(mutex);
V(empty);
Consume The item in NextC; // 消费一个数据
} while(TRUE)
}
继续分析
P(empty);语句与P(mutex);语句是否可以互换?
答案是不行;
当缓冲池已满,且mutex=1时(此情况合理),若此时再执行P进程,则先执行P(mutex);,此时mutex--,mutex的值变为0,接着执行P(empty);,由于empty=0,无法继续执行,将此P进程加载至阻塞队列。此时mutex=0,若此时执行C进程,首先执行P(full);,缓冲池存在数据可以获取,因此接着执行P(mutex);,由于mutex=0,所以阻塞,将此进程加载至阻塞队列。之后无论如何执行C进程都会加载至阻塞队列,导致死锁。
2. 读者写者问题
问题描述
存在若干读者,若干写者和一个数据区(可视为一个变量buffer)。允许多个读者同时读取数据区的值,但是当一个写者向数据区写入数据时,不允许其他任何人对数据区进行操作,无论是读者还是写者。(假设初始时数据区存在数据)
分析
“当一个写者向数据区写入数据时,不允许其他任何人对数据区进行操作”表明多个writer进程之间为互斥关系,writer进程和reader进程之间也为互斥关系。多个reader进程之间没有同步或互斥关系,因为允许同时多个读操作。
看似只需要一个mutex控制是否存在写操作,若存在写操作,通过P(mutex)控制其他程序无法进行,当写操作结束执行V(mutex)操作。但是若先执行reader进程呢?第一个读者开始读,即抢占了CPU的执行权,显然此时写者无法进行写操作,因此写者需要等待读者的读操作执行完成。何时读操作完成?由题意知,允许多个读者同时读取数据,所以存在读者一个接一个地进行读取操作的情况,那么如何判断这一系列读操作是否彻底完成,即写操作何时可以开始?
为解决这一问题,我们设置变量:rmutex控制reader进程,wmutex控制writer进程,readcount记录同时进行读操作的读者个数。
其中readcounter对于多个读者来说,应视为临界资源,所以应有一个互斥信号量,即rmutex。
也可以理解举例理解,假设不存在rmutex信号量,若多个读者进程开始执行,在执行readcounter++之前多个读者进程判断readcounter==0均为真,使得wmutex信号量多次进行P操作,导致wmutex.value多次进行--操作。而执行到readcounter--只有最后一个读者进行执行完--后,才会满足readcounter==0的判断,才会对wmutex信号量进行V操作,这导致wmutex.value始终小于0,致使死锁。因此,需要用对rmutex信号量的P,V操作将其包裹成“原语”。
还有同学可能疑惑为什么readcounter不能作为信号量,而要作为一个通过rmutex信号量控制的普通变量?
这是因为,多个读者进程之间并不存在互斥或者同步关系。设置信号量的根本原因在于解决同步或互斥情况下数据共享(并发)导致的不可再现性。由于多读者进程不存在互斥或同步关系,所以无法通过设置信号量来控制。
代码
通过代码来理解过程吧!
semaphore rmutex = 1, wmutex = 1;
int readcount = 0;
void reader(){
do {
P(rmutex); // 判断此读者是否可以读取数据,若可以读则继续执行代码,反之进入阻塞队列
if(readcount == 0) P(wmutex); // 若此读者为第一个读者(将CPU控制权抢到手的读者),则CPU控制权归读者所有,因此要让写操作阻塞,wmutex.value--,即调用P原语
readcount ++; // 读者数加一
V(rmutex); // 这个很关键,看似和“perform read operation;”语句下的“P(rmutex);”一样可有可无,但是此代码与上面的“P(rmutex);”匹配,在这两句代码之间的代码块类似于原语。当存在多个读者进行读操作时也不会在此块代码中交错。下同。
... ...
perform read operation; // 进入临界区,进行读操作
... ...
P(rmutex);
readcout --; // 读操作结束,读者数减一
if(readcout == 0) V(wmutex); // 若此读者为最后一个读者,则写者又有机会抢夺CPU的执行权了
V(rmutex); // 与上面的“P(rmutex);”匹配,作用同上。
}while(TRUE)
}
void writer(){
do {
P(wmutex);
... ...
perform write operation;
... ...
V(wmutex);
}
}
3. 哲学家进餐问题
问题描述
该问题是描述有五个哲学家共用一张圆桌,分别坐在周围的五张椅子上,在圆桌上有五个碗和五只筷子,他们的生活方式是交替地进行思考和进餐。平时,一个哲学家进行思考,饥饿时便试图取用其左右最靠近他的筷子,只有在他拿到两只筷子时才能进餐。进餐完毕,放下筷子继续思考。
分析
很显然,每个筷子都是一个临界资源,每位哲学家都是一个进程,每个相邻的进程存在着互斥的关系。因此对于每一个临界资源都需要设置一个信号量来控制。
代码
semaphore chopstick[5] = {1,1,1,1,1};
void philosophers()
{
do {
p(chopstick[i]);
p(chopstick[(i+1)%5]);
eat for a while; //临界资源
v(chopstick[i]);
v(chopstick[(i+1)%5]);
think for a while;
} while(TRUE)
}
继续分析
当哲学家饥饿时,总是先去拿他左边的筷子,即执行P(chopstick[i]);然后再去拿他右边的筷子,即执P(chopstick[(i+1)%5]);最后便可进餐。进餐完毕,又先放下他左边的筷子,然后再放右边的筷子。
上述解法可保证不会有两个相邻的哲学家同时进餐,但有可能引起死锁。假如五位哲学家同时饥饿而各自拿起左边的筷子时,就会使五个信号量chopstick均为0;当他们再试图去拿右边的筷子时,都将因无筷子可拿而无限期地等待。
对于死锁问题,可采取以下几种解决方法:
-
至多只允许有四位哲学家同时去拿左边的筷子,最终能保证至少有一位哲学家能够进餐,并在用毕时能释放出他用过的两只筷子,从而使更多的哲学家能够进餐。
-
仅当哲学家的左、右两只筷子均可用时,才允许他拿起筷子进餐。
-
规定奇数号哲学家先拿他左边的筷子,然后再去拿右边的筷子,而偶数号哲学家则相反。按此规定,将是1、2号哲学家竞争1号筷子;3、4号哲学家竞争3号筷子。即五位哲学家都先竞争奇数号筷子,获得后,再去竞争偶数号筷子,最后总会有一位哲学家能获得两只筷子而进餐。
对应伪代码:https://blog.csdn.net/x1114832836/article/details/90670334
4. 一道考研题
问题描述
三个进程 P1、P2、P3互斥使用一个包含 N(N>0)个单元的缓冲区。P1 每次用 produce()生成一个正整数并用 put()送入缓冲区某一空单元中;P2每次用 getodd()从该缓冲区中取出一个奇数并用countodd()统计奇数个数;P3每次用geteven()从该缓冲区中取出一个偶数并用counteven()统计偶数个数。请用信号量机制实现这三个进程的同步与互斥活动,并说明所定义信号量的含义。要求用伪代码描述。
分析
生产者消费者问题的变式,难点在于代码的书写,正确代码的书写需要基于准确信号量的定义。
定义信号量 odd 控制 P1 与 P2 之间的同步;even 控制 P1 与 P3 之间的同步;empty 控制生产者与消费者之间的同步;mutex 控制进程间互斥使用缓冲区。
重点是看出put()、getodd()和geteven()都是对缓冲区(临界资源)进行操作,因此需要通过互斥信号量控制,且只需要将访问临界资源的部分包裹起来即可。
代码
semaphore odd = 0, even = 0, empty = N, mutex = 1;
P1( ){
x = produce(); // 生成一个数
P(empty); // 判断缓冲区是否有空单元
P(mutex); // 临界资源是否被占用
Put();
V(mutex); // 释放缓冲区
if(x%2==0)
V(even); // 若为偶数,向P3发出信号
else
V(odd); // 若为奇数,向P2发出信号
}
P2( ){
P(odd); // 收到P1发来的信号,已产生一个奇数
P(mutex); // 缓冲区是否被占用
getodd();
V(mutex); // 释放缓冲区
V(empty); // 向P1发信号,多出一个空单元
countodd();
}
P3( )
{
P(even); // 收到P1发来的信号,已产生一个偶数
P(mutex); // 缓冲区是否被占用
geteven();
V(mutex); // 释放缓冲区
V(empty); // 向P1发信号,多出一个空单元
counteven();
}
评分说明
- 能正确给出互斥信号量定义与含义的,给 1 分。
- 能正确给出 3 个同步信号量定义与含义的,各给 1 分,共3 分。
- 能正确描述 P1、P2 和 P3 进程活动的,各给 1 分,共 3分。
- wait()、signal()等同于 P、V。
5. 过独木桥问题
问题描述
东西向汽车过独木桥,为了保证安全,只要桥上无车,则允许一方的汽车过桥,待一方的车全部过完后, 另一方的车才允许过桥。请用信号量和 P、V操作写出过独木桥问题的同步算法。
分析
这是一道“读者写者问题”的变形问题。两侧的车抢占独木桥资源,先抢占到的一侧的车先通行,直至一侧的车全部通过,另一侧才有机会再次竞争独木桥资源。
显然,独木桥为两侧车辆的互斥资源,而同侧的车之间没有直接的约束关系,类似于两侧都是读者,但是两侧的读者会抢占互斥资源。
首先为独木桥设置一个互斥信号量bridge。
countA、countB分别表示A侧,B侧在桥上的车辆。
由于countA、countB分别对于A侧和B侧车而言为共享资源,所以也要为这两个变量分别设置两个互斥信号量,保证A侧(B侧)有一辆车过桥对count修改时,再有同侧的车过桥时,先让前一辆车对count ++后再通过。因此用mutexA控制countA,mutexB控制countB。
代码
semaphore bridge = 1;
int countA = 0;
semaphore muetxA = 1;
int countB = 0;
semaphore mutexB = 1;
processA(){
while(1){
P(mutexA);
if(countA == 0) P(bridge);
countA ++;
V(mutexA);
// 上桥
// 过桥
// 下桥
P(mutexA);
countA --;
if(countA == 0) V(bridge);
V(mutexA)
}
}
processB(){
while(1){
P(mutexB);
if(countB == 0) P(bridge);
countB ++;
V(mutexB);
// 上桥
// 过桥
// 下桥
P(mutexB);
countB --;
if(countB == 0) V(bridge);
V(mutexB)
}
}
6. 读书
问题描述
有一阅览室,共有100个座位。读者进入时必须先在唯一的一张登记表上登记信息。读者离开时要消掉登记信息。试用P、V操作描述读者进程的同步结构。
分析
重点是“唯一”,这就得考虑多个读者进入阅览室时,要互斥地登记个人信息,因此登记表为临界资源,需要互斥访问,mutex控制互斥。
每个读者之间需要相互通信告知是否还有空位,empty控制通信,初值为100。
代码
semaphore empty=100, mutex=1;
void reader() {
while(true) {
P(empty);
P(mutex);
登记个人信息;
V(mutex);
就坐读书;
P(mutex);
删除个人信息;
V(mutex);
V(empty);
}
}
7. 两个盘吃水果,父亲给儿子梨,母亲给女儿苹果
问题描述
一家四口爸爸、妈妈、儿子、女儿,使用两个能容纳一个水果的盘子。爸爸每次准备一个梨放进盘子,妈妈每次准备一个苹果放进盘子,儿子只吃梨,女儿只吃苹果。
分析
两个盘子是临界资源,父亲、母亲、儿子和女儿都要互斥地访问盘子,互斥信号量mutex;
父亲和母亲类似于生产者,儿子和女儿类似于消费者;
但是因为儿子只能接受父亲的梨,女儿只能接受母亲的苹果,因此需要通过两个信号量分别表示两个盘子中梨和苹果的个数,这样就实现了父母向儿女的通信;
为实现儿女向父母的通信,需要使用信号量empty控制空盘子的数量。
代码
semaphore empty=2,mutex=1,apple=0,pear=0;
void father(){
do{
P(empty); //等待空盘子
P(metux); //等待获取对盘子的操作
爸爸向盘中放一个梨;
V(mutex); //释放对盘子的操作
V(pear); //通知儿子可以来盘子中取苹果
}while(TRUE);
}
void mather(){
do{
P(empty); //等待空盘子
P(metux); //等待获取对盘子的操作
妈妈向盘中放一个苹果;
V(mutex); //释放对盘子的操作
V(apple); //通知女儿可以来盘子中取苹果
}while(TRUE);
}
void son(){
do{
P(pear); //判断盘子中是否有梨
P(metux); //等待获取对盘子的操作
儿子取出盘中的梨;
V(mutex); //释放对盘子的操作
V(empty); //存在空盘子,可以继续放水果了
}while(TRUE);
}
void daugther(){
do{
P(apple); //判断盘子中是否有苹果
P(metux); //等待获取对盘子的操作
女儿取出盘中的苹果;
V(mutex); //释放对盘子的操作
V(empty); //存在空盘子,可以继续放水果了
}while(TRUE);
}
8. 一个盘吃水果,父亲给儿子梨,母亲给女儿苹果
问题描述
一家四口吃水果的问题。假设只有一只盘子,盘子里一次只能放一个水果。爸爸每次挑一个梨放进盘子,妈妈每次挑一个苹果放进盘子。儿子每次只从盘子里取一个梨吃,女儿每次只从盘子里取一个苹果吃。每个人循环做同样的事情。
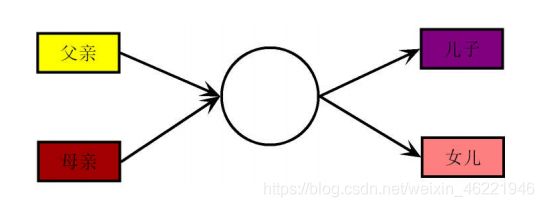
分析
思路一: 解决了上面的两个盘子吃水果的问题,我们可以类比的写出一个盘子的代码。
思路二: 其实可以用三个信号量来控制。不用加上empty信号量,因为它控制空盘子的数目,空盘子数目要么是1要么是0,与互斥信号量mutex无异,因此也可以采用三信号量来控制,但是代码会稍微难写一点。
代码
思路一
semaphore empty=1,mutex=1,apple=0,pear=0;
void father(){
do{
P(empty); //等待盘子为空
P(metux); //等待获取对盘子的操作
爸爸向盘中放一个梨;
V(mutex); //释放对盘子的操作
V(pear); //通知儿子可以来盘子中取苹果
}while(TRUE);
}
void mather(){
do{
P(empty); //等待盘子为空
P(metux); //等待获取对盘子的操作
妈妈向盘中放一个苹果;
V(mutex); //释放对盘子的操作
V(apple); //通知女儿可以来盘子中取苹果
}while(TRUE);
}
void son(){
do{
P(pear); //判断盘子中是否有梨
P(metux); //等待获取对盘子的操作
儿子取出盘中的梨;
V(mutex); //释放对盘子的操作
V(empty); //盘子空了,可以继续放水果了
}while(TRUE);
}
void daugther(){
do{
P(apple); //判断盘子中是否有苹果
P(metux); //等待获取对盘子的操作
女儿取出盘中的苹果;
V(mutex); //释放对盘子的操作
V(empty); //盘子空了,可以继续放水果了
}while(TRUE);
}
思路二
semaphore mutex=1,apple=0,pear=0;
void father(){
do{
P(metux);
放梨;
V(pear);
}while(TRUE);
}
void mather(){
do{
P(metux);
放苹果;
V(apple);
}while(TRUE);
}
void son(){
do{
P(pear);
拿梨;
V(mutex);
}while(TRUE);
}
void daugther(){
do{
P(apple);
拿苹果;
V(mutex);
}while(TRUE);
}
9. 五进程合作
问题描述
如下图所示,有5个进程合作完成某一任务。用wait (或P)、 signal(或V)操作实现,写出算法描述。
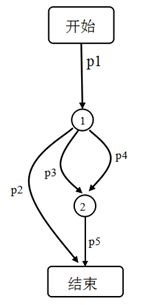
分析
首先要理解题意,“合作完成某一任务”,这说明需要P2和P5都执行结束才算任务结束。同理P3和P4都执行完成才能开启P5的执行。这说明P3和P4并非互斥地使用资源1,而是需要P1生产足够的资源1以保证P3和P4并行。P2同理。
设置四个信号量:si=0表示Pi是否结束,i=1~4
代码
semaphore s1=0, s2=0, s3=0, s4=0;
P1() {
while(true) {
执行P1;
V(s1); // 需要生产3个资源1保证P2、P3和P4均能并行
V(s1);
V(s1);
}
}
P2() {
while(true) {
P(s1);
执行P2;
}
}
P3() {
while(true) {
P(s1);
执行P3;
V(s3);
}
}
P4() {
while(true) {
P(s1);
执行P4;
V(s4);
}
}
P5() {
while(true) {
P(s3); // P3和P4都完成,执行P5
P(s4);
执行P5;
}
}
