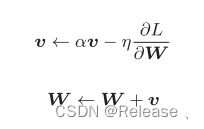深度学习笔记
一、 数值微分
d f ( x ) d x = lim h → 0 f ( x + h ) − f ( x ) h \frac{\mathrm{d} f(x)}{\mathrm{d} x}= \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} dxdf(x)=h→0limhf(x+h)−f(x)
求导公式表示瞬间的变化量,在python中可以定义为
def numerical_diff(f,x):
h = 10e - 50
return (f(x+h) - f(x)) / h
参数f代表函数,x代表自变量,想要h尽可能接近0,所以h使用了10e-50,但是这样反而会产生舍入误差。在python中舍入误差表示为
np.float32(1e-50) # 输出 0.0
无法正确的表示出来。但是最开始设定h=1e-50,(x+h)和x之间的斜率仍和真正的斜率之间是不一致的,因为h是人为设定,永远不可能无限接近于0。
所以可以计算(x+h)和(x-h)之间的差分,以x为中心,计算左右的差分,也叫中心差分。
def numerical_diff(f,x):
h = 1e-4 #0.01
return (f(x+h) - f(x-h)) / (2*h)
所以,利用微小的差分求导数的过程叫做数值微分(numerical differentiation)
d f ( x ) d x = lim h → 0 f ( x + h ) − f ( x − h ) 2 h \frac{\mathrm{d} f(x)}{\mathrm{d} x}= \lim_{h \to 0}\frac{f(x+h)-f(x-h)}{2h} dxdf(x)=h→0lim2hf(x+h)−f(x−h)
二、 梯度
f ( x 0 , x 1 ) = x 0 2 + x 1 2 f(x_{0},x_{1}) = x_{0}^{2}+x_{1}^{2} f(x0,x1)=x02+x12
( ∂ f ∂ x 0 , ∂ f ∂ x 1 ) (\frac{\partial f}{\partial x_{0}} , \frac{\partial f}{\partial x_{1}}) (∂x0∂f,∂x1∂f)
f(x)同时对(x0, x1)求偏导,这样由全部变量的偏导数的汇总而成的向量成为梯度。
def numerical_gradient(f,x):
h = 1e-4
grad = np.zero_like(x) # 生成一个形状和x相同、所有元素都为0的数组
for idx in range(x.size):
tep_val = x[idx]
#实现 f(x+h)
x[idx] = tep_val + h
fxh1 = f(x)
#实现 f(x-h)
x[idx] = tep_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tep_val
return grad
从导数到偏导数,也就从曲线来到了曲面上,f(x0,x1)对x0求偏导,就是在x1位置上不变,沿x0轴方向的变化率,f(x0,x1)对x1求偏导同理。
这里我们对(3,4),(0,2),(3,0)求梯度
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.]) #说明在 x0=3 的时候在x0正方向上的斜率是6
>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([ 0., 4.])
>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([ 6., 0.])
#在(3,4)出的梯度是(6,8),NumPy数组,数值会被更改为"易读模式",实际是 [6.0000000000037801, 7.9999999999991189]
按照元素值为负梯度的向量画出箭头,梯度指向了函数值降低的方向。
梯度会指向各点函数值减小最多的方向
每一个方向导数的值代表了在该方向上的变化程度,我们要寻找在某点处函数变化最快的方向就可以转化成寻找在该点处方向导数的绝对值最大时对应的那个方向。( 偏导的绝对值越大,变化越大)
三、 梯度法
神经网络必须在学习时招待最优参数(权重和偏置),即使损失函数最小时的参数。
梯度表示的是各点处函数值减小最多的方向。
但是无法保证梯度所指的方向就是函数的最小值或者真正该前进的方向
函数极小(大)值以及鞍点处梯度为0,梯度法就是为了找到梯度为0的点,但是此时并不能保证是梯度为0的地方就是最值。
但是!沿着梯度方向能够最大限度地减小函数的值。所以以梯度为线索,决定前进的方向
梯度法:
函数的取值从当前位置沿着梯度方向前进一定距离, 然后在新的方向重新求梯度,再沿着新梯度方向前进,如此反复。像这样,通过不断沿着梯度方向前进,逐渐减小函数值的过程就是梯度法
用数学公式表示梯度法

其中η表示学习率,学习率决定再一次学习中,应该学习多少,以及在多大程度上更新参数。
学习率需要事先确定为某个值。再神经网络中,一般一边改变学习率的值,一边确认学习是否正确进行了。
python实现梯度下降法
def gradient_descent(f,init_x,lr = 0.01 , step_num = 100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr * grad
return x
# 参数f是要进行最优化的函数,init_x是初始化,lr是学习率,step_num是梯度法的重复次数。
# numerical_gradient(f,x)会求函数的梯度,用该梯度乘以学习率得到进行更新操作,由step_num指定重复次数。
如果学习率过大的话,会发散成一个很大的值,但是如果过小的话,基本不会有什么更新。所以像学习率这样的超参数,需要尝试多个值,以便找到一种可以使学习顺利进行的设定。
四、神经网络的梯度
import numpy as np
import sys, os
sys.path.append(os.pardir)
from Function import softmax, cross_entropy_error, numerical_gradient
class simpleNet:
def __init__(self):
self.w = np.random.randn(2, 3) # 用高斯分布随机进行初始化
def predict(self, x):
return np.dot(x, self.w)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
net = simpleNet()
print(net.w)
x = np.array([0.6, 0.9])
p = net.predict(x) # 得到的仍然是一个矩阵
print(p)
print(np.argmax(p)) # 找到最大元素的下表
t = np.array([0, 0, 1]) # 正确解的标签
print(net.loss(x, t)) # 计算损失函数
def f(w): # 梯度下降方法里面需要传入一个 函数 , 返回函数的功能
return net.loss(x, t)
dw = numerical_gradient(f, net.w) # 使用梯度下降求出 W 权重矩阵里面的所有梯度下降
print(dw)
function.py
import numpy as np
# 激活函数 softmax函数
def softmax(x):
c = np.max(x)
exp_a = np.exp(x - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
# 梯度下降法
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同的数组
for idx in range(len(x)):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 还原值
return grad
# 求交叉熵
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
五、学习算法的实现
神经网络存在合适的权重和偏置,调整权重和偏置以方便你和训练数据的过程叫做“学习”
步骤1:mini-batch
从训练数据中随机选出一部分数据,这部分数据称为mini-batch。我们
的目标是减小mini-batch的损失函数的值。
步骤2:计算梯度
为了减小mini-batch的损失函数的值,需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。
步骤3:更新参数
将权重参数沿梯度方向进行微小更新。
步骤4:重复
重复步骤1、步骤2、步骤3。
5.1 二层神经网络的类
import sys, os
import numpy as np
sys.path.append(os.pardir)
import Function
from Function import softmax, cross_entropy_error, numerical_gradient, sigmoid
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
w1, w2 = self.params['w1'], self.params['w2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(x, w2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
# axis = 0 是按每列找最大的元素下标
# axis = 1 是按每行找最大的元素下标 ,返回的是按 行/列 的一维的列 表
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
# lambda匿名函数定义了一个函数f,参数是w,函数体是冒号后面的部分
# 相当于是
# def f(w):
# return self.loss(x,t)
loss_W = lambda W: self.loss(x, t)
#函数 numerical_gradient中参数x传入的是一个函数
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads

在 TwolayerNet 中有 pareams 和 grads 两个字典型实例变量,params 中保存了权重参数。
5.2 mini-batch的实现
所谓的 mini-batch 就是从训练数据中随机选择一部分数据,,再将这些 mini-batch 为对象,使用梯度法更新参数的过程。
以TwoLayernet 类为对象,使用MNIST数据集进行学习
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_laobel = True)
train_loss_list = [] #损失精度列表
train_acc_list = [] # 训练精度列表
test_acc_list = [] # 测试精度列表
# 平均每个epoch的重复次数,最少重复一次
iter_per_epoch = max(train_size / batch_size, 1)
# 超参数
iters_num = 10000
batch_size = 100
learning_rate = 0.1
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 获取mini-batch
#random.choice() 代表从
batch_mask = np.random.choice(train_size, batch_size)
# 从train_size 中随机选取batch_size个内容
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 高速版!
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 计算每个epoch的识别精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
注解:
① epoch 是一个单位,表示学习中所有训练数据均被使用过一次的更新次数。比如 10000笔训练数据,batch_size 为100 重复随机梯度下降法100粗,所有的训练数据就都被看过了。这100 次就是一个 epoch
② train_size : 可以理解为有1000张图片,每张图片是28 x 28的,那么训练集就有三个属性(1000,28,28),代表有1000张图片,每张图片是28 x 28的,而shape[0]代表的是提取出来1000,代表有1000张图片。
③batch_mask:随机在train_size中选取batch_size大小的元素返回一个 列表
④x_batch : x_train列表中再嵌套一个列表,返回的仍是一个列表
t_batch相当于是一个batch_size大小的一个列表,里面存放的是正确的标签,相当于监督数据,将正确的标签设置为1,其余为0。标签列表的长度取决于你要分多少个种类。
六、学习优化
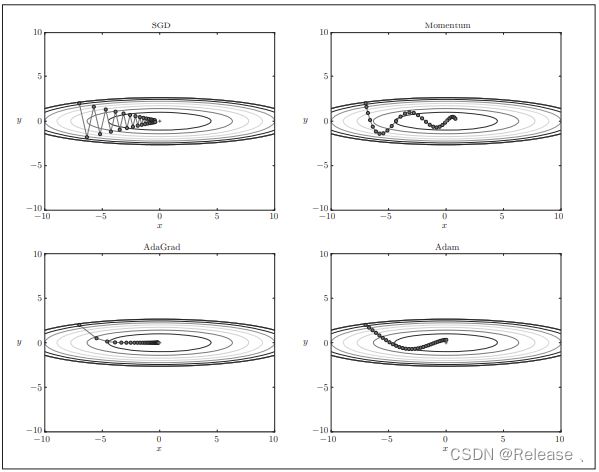
SGD :
前面方法使用参数的梯度,沿梯度方向更新参数,重复这个步骤,逐步靠近最优参数,称随机梯度下降法(SGD)
缺点:如果函数的形状是非均向的,入延申状,搜索的路径就会非常低效,原因是梯度方向并没有指向最小值方向,而是反复走了很多弯路。
Momentum:
七、权重的初始值
不能将权重初始值设为一样的,因为再反向传播中,所有值都会进项相同的更新,叫做’权重均一化’,所以必须随机生成初始值。
7.1过拟合
发生过拟合的原因,主要有两点
①:模型拥有大量的参数、表现力强
②:训练数据少
抑制过拟合的方法:
①:权值衰减:通过在学习的u欧城中对打的权重进行惩罚,来一直过拟合,很多过拟合原本就是因为权重参数取值过大菜发生的。
例如,对于所有权重,权值衰减法都会为损失函数加上 1 2 λ W 2 \frac{1}{2}\lambda W^{2} 21λW2作为权值衰减。λ就是控制正则化强度的超参数,设置的越大,对大的权重施加的惩罚就越重。
这种方式如果应对复杂的网络模型,就很难应对了
②Dropout:是一种在学习的过程中随即删除神经元的方法。训练时,随机选出隐藏层的神经元,然后将其删除。被删除的舍宁与那不再进行信号的传递。

用代码实现Dropout:
class Dropout:
def __init__(self, dropout_ratio = 0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg = True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
注解:正向传播时, self.mask 中都会以False 的形式保存要删除的神经元。并且会随机生成和 x 形状相同的数组,并将值比dropout_ratio大的元素设置为True。
7.2超参数,测试数据
神经网络中,除了权重和偏置参数,其余大多为超参数,如各层神经元数量,batch大小,参数更新时的学习率和权值衰减等。
需要注意的是:不能使用测试数据评估超参数的性能,因为如果使用测试数据调整超参数,超参数的值会对测试数据发生过拟合。用测试数据确认超参数的值的好坏,就会导致超参数的值被调整为只拟合测试数据。这样的话就会得到不能拟合其他数据、泛化能力低的模型。
所以,调整超参数,必须使用超参数专用的确认数据,一般称为验证数据。
训练数据用于参数(权重和偏置的学习),验证数据用于超参数的性能评估。
根据不同的数据集,有的会事先分成训练数据、验证数据、测试数据,有的分成熟练数据和测试数据,有的不分割。
自我进行分割:
(x_train, t_train), (x_test, t_test) = load_mnist()
# 打乱训练数据
x_train, t_train = shuffle_dataset(x_train, t_train)
# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num] #数据切片,默认从1开始到validation_num结束
t_val = t_train[:validation_num]
x_train = x_train[validation_num:] # 从validation_num开始
t_train = t_train[validation_num:]
超参数的优化步骤:
步骤0
设定超参数的范围。
步骤1
从设定的超参数范围中随机采样。
步骤2
使用步骤1中采样到的超参数的值进行学习,通过验证数据评估识别精度(但是要将epoch设置得很小)。
步骤3
重复步骤1和步骤2(100次等),根据它们的识别精度的结果,缩小超参数的范围
八、卷积神经网络
8.1 整体结构
首先CNN和神经网络一样,通过堆叠组装层来构建。但是他多了卷积层(Convolution层)和池化层(Pooling层)。
在神经网络中,相邻层的所有神经元之间都有连接,成为全连接,另外用Affine层实现了全连接层。

在CNN中增加了卷积层和池化层。

全连接层输入数据是图像时,图像通常是高、长、通道方向上的3维数据拉平为1维数据,忽视形状。
但是卷积层可以保持形状不变。当输入数据是图像是,卷积层会以3维数据的行书接受输入数据,并同样以3维数据的形式输出至下一层。所以在CNN中可以正确理解图像等具有形状的数据。
另外,CNN中将卷积层的输入输出数据成为特征图。卷积层的输入数据成为输入特征图,输出数据成为输出特征图。
学会计算卷积 和 填充 和 步幅
填充的作用:每次卷积都会缩小空间,在某个时刻输出大小可能变为1,导致无法在应用卷积运算,为了避免这个,所以要进行填充。
3维数据的卷积运算:
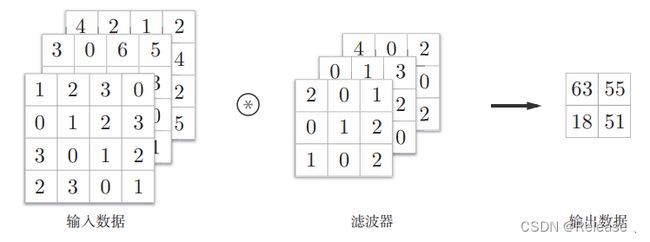
通道方向上有多个特征图时,会按照通道进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。
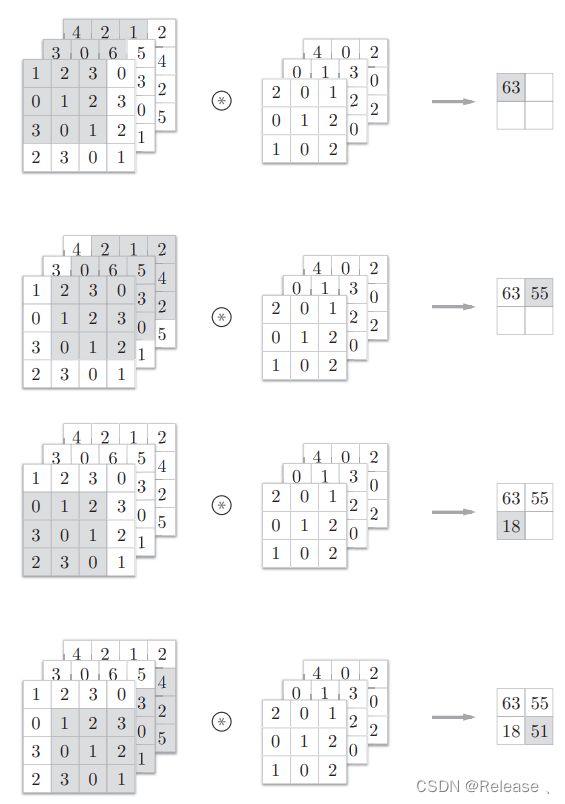
在多维的卷积运算中,输入数据和滤波器的通道数要设为相同的值。
8.2 池化层
池化是缩小高、长方向上的空间的运算。
池化层的特点:
没有要学习的参数:
池化层和卷积层不同,没有要学习的参数。池化只是从目标区域中取最大值(或者平均值),所以不存在要学习的参数
通道数不发生变化
经过池化运算,输入数据和输出数据的通道数不会发生变化。
对微小的位置变化具有鲁棒性(健壮)
输入数据发生微小偏差时,池化仍会返回相同的结果。因此,池化对输入数据的微小偏差具有鲁棒性。
九、卷积层和池化层的实现
9.1 基于im2col的展开
用for循环实现卷积运算,估计要重复很多个for语句,所以考虑使用im2col便利的函数实现。
对3维的输入数据应用im2col,数组转变为2维矩阵。其中4维数据就是多个三维数据堆叠而成。

实现流程:

python实现池化层:
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
#h:高 , w:长 , stride:步幅 , pad:填充
# 展开(1)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
# 最大值(2)
out = np.max(col, axis=1)
# 转换(3)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
return out
9.2、CNN的实现
input_dim―输入数据的维度:(通道,高,长)
conv_param―卷积层的超参数(字典)。字典的关键字如下:
filter_num―滤波器的数量
filter_size―滤波器的大小
stride―步幅
pad―填充
hidden_size―隐藏层(全连接)的神经元数量
output_size―输出层(全连接)的神经元数量
weitght_int_std―初始化时权重的标准差
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),conv_param={'filter_num':30,'filter_size':5,'pad':0, 'stride':1},hidden_size=100,output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) *(conv_output_size/2))
# 计算卷积层的输出大小
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num,input_dim[0] , filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size,hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 各层实现
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'],self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'],self.params['b3'])
self.last_layer = softmaxwithloss()
# 所以预测函数和损失函数重新定义
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
# 反向传播求梯度
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
提高识别精度的技术:集成学习,学习率衰减,Data Augmentation(数据扩充),尤其是数据扩充,简单且效果明显。
Data Augmentation 人为地看哟冲输入图像,如施加旋转、垂直或水平方向上地移动等微笑变化,增加图像的数量,增加亮度,放大缩小尺度上的变化。
9.3、 加深层的动机
层数越高,识别性能也越高。
加深层 可以减少网络的参数数量。 通过加深层,可以减少学习数据,使学习更加高效。
在前面的卷积层中,神经元会对边缘等简单的形状有响应,随着层的加深,开始对纹理,物件部分等更加复杂的东西有响应。
VGG 、GoogLeNet 、ResNet 网络,但是VGG是其中最简单的且最多受用的。
9.4、分布式学习
深度学习伴随这很多试错、比较耗费事件,为了进一步提高深度学习所需的计算的速度,可以考虑在多个GPU或者多台机器上进行分布式计算。其中Google 的TensorFlow、微软的CNTK在开发过程中高度重视分布式学习。