数字图像处理知识点梳理——第十一章 表示和描述
文章目录
- 一、引言
- 二、表示
-
- 1. 边界追踪
-
- 2. 链码
- 3. 多边形近似
- 4. 标记图
- 5. 边界线段
- 6. 骨架
- 三、边界描绘子
-
- 1. 一些简单的描绘子
- 2. 形状数
- 3. 傅里叶描绘子
- 4. 统计矩
- 四、区域描绘子
-
- 1. 一些简单的描绘子
- 2. 拓扑描绘子
- 3. 纹理
- 4. 不变矩
- 五、使用主分量进行描绘
- 六、关系描绘子
一、引言
“表示”的方法:
(1)根据其外部特征(其边界)来表示区域
(2)根据其内部特征(如组成该区域的像素)表示
当我们关注的重点是形状特征时,可选外部表示;
关注的重点是内部属性如颜色和纹理时,可选内部表示。
选择一种表示方法之后描述区域。选择的方法应满足:描绘子的特征应尽可能地对大小、平移和旋转不敏感。
二、表示
本章中的算法要求一个区域的边界上的点以顺时针(或逆时针)方向排序,且仅限讨论单个区域,通过单独的处理各个区域扩展到多个不相交的区域。
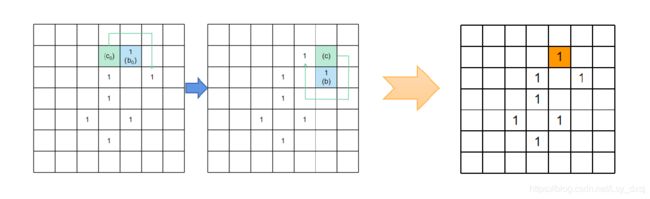
1. 边界追踪
边界追踪可能会因为满足停止规则而导致错误,比较适合用来提取孔洞。
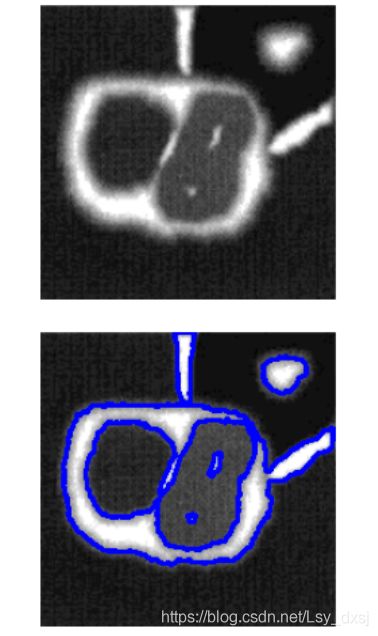
opencv自带的轮廓跟踪和绘制:
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
img = cv2.imread('C:/Users/13121/Desktop/11.png')
plt.imshow(img)
plt.axis('off')
plt.show()
grayImg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret,binImg = cv2.threshold(grayImg, 100, 255, cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binImg, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(img, contours, -1, (0, 0, 255), 2)
plt.imshow(img)
plt.axis('off')
plt.show()
hierarchyDF = DataFrame(hierarchy[0], columns = ['pre', 'next', 'child', 'parent'])
#轮廓检测
cv2.findContours(image, mode, method, contours=None, hierarchy=None, offset=None)
cv2.RETR_TREE 建立一个等级树结构的轮廓。
cv2.CHAIN_APPROX_SIMPLE 压缩水平方向,垂直方向,对角线方向的元素,只保留该方向的终点坐标,例如一个矩形轮廓只需4个点来保存轮廓信息。
#轮廓绘制
cv2.drawContours(image, contours, contourIdx, color, thickness=None, lineType=None, hierarchy=None, maxLevel=None, offset=None)
contourIdx:指定绘制轮廓list中的哪条轮廓,如果是-1,则绘制其中的所有轮廓。
thickness:表明轮廓线的宽度,如果是-1(cv2.FILLED),则为填充模式。
thickness=1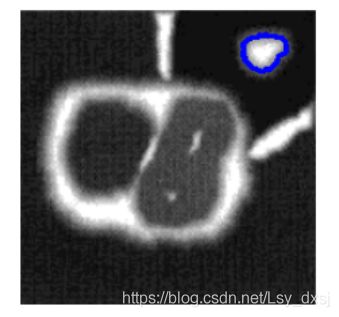
thickness=2
thickness=3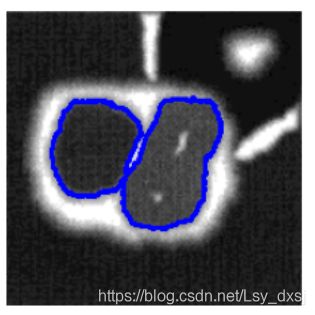
2. 链码
链码是一种边界的编码表示法,一般描述的是边界点集。包括4-链接和8-链接。8-链接的边界描述性更好,因此最常用的是8-链接。

(4-链接)
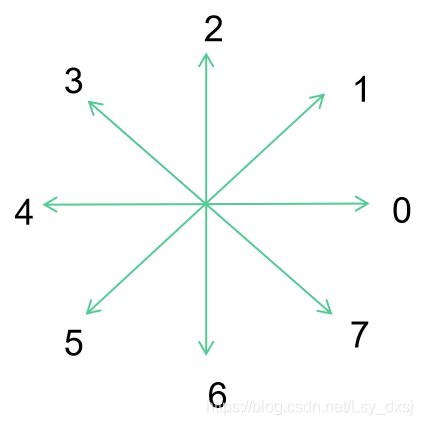
(8-链接)
算法:从起点开始,沿边界编码,至起点被重新碰到,结束一个对象的编码。
| 问题 | 解决方法 |
|---|---|
| 链码非常长 | 加大网格间距来对边界重取样 |
| 噪声或不完美分割会对链码产生干扰 | 依据原始边界与结果的接近程度来确定新点的位置 |
| 产生不同链码的原因 | 改进方法 |
|---|---|
| 不同的起始点导致出现不同的链码 | 进行起始点归一化处理,比如取最小的码作为归一化结果 |
| 不同的编码方向导致出现不同的链码 | 使用链码的首差代替码字本身 |
| 图像旋转导致链码改变 | 进行旋转归一化处理,比如采用一阶差分作为新的码。 |
例如针对情况三:
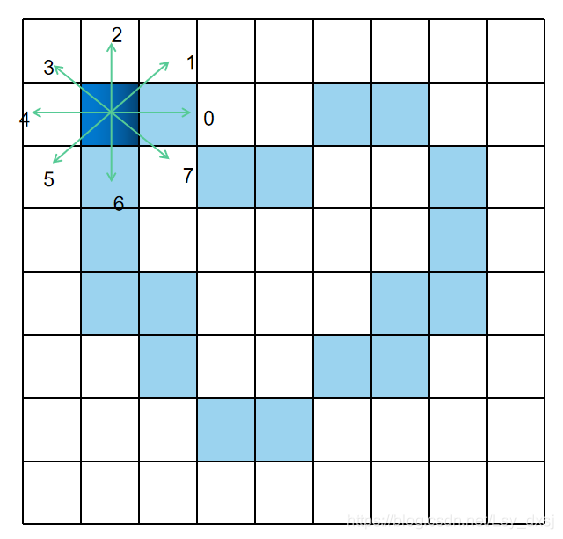
0701076646454324222(原图8-链码)
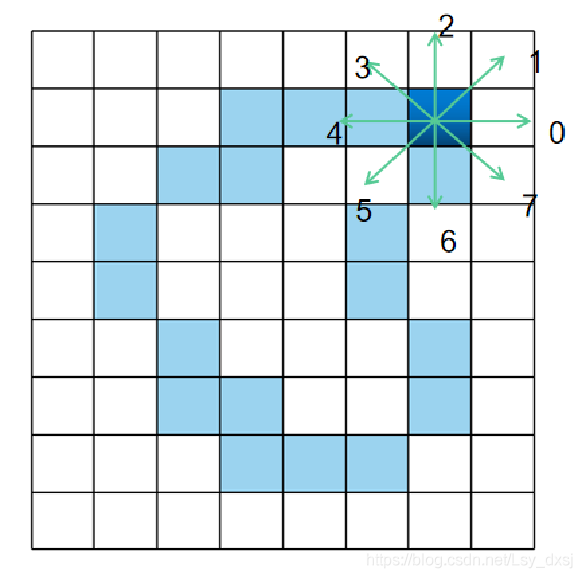
6567654424232102000(旋转后8-链码)
使用一阶差分后的8-链码均为:6711777062617772600
链码对单个对象不适用,一般用于一幅图像中有多个对象的情况。
3. 多边形近似
思想:单元的大小决定着多边形近似的精度,使用尽可能少的线段数来获取给定边界的基本形状。
点合成法:
1)沿着边界选两个相邻的点,计算首尾连接直线段与原始折线段的误差R
2)如果误差小于预先设置的阈值T,则去掉中间点,选新点对与下一相邻点对,重复1);否则,存储线段的参数,置误差为0,选被存储线段的终点为起点,重复1)2)
3)当程序的的第一个起点被遇到,程序结束

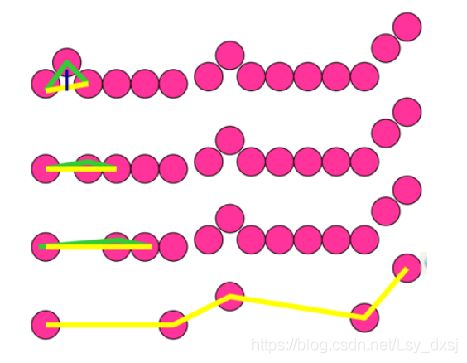
点合成法存在的问题:顶点一般不对应于边界的拐点(如拐角),因为新的线段直到超过误差的阈值才开始。
边分裂算法:
1)连接边界线段的两个端点(如果是封闭边界,连接最远点)
2)如果最大正交距离大于阈值,将边界分为两段,最大值点定位一个顶点,重复1)
3)如果没有超过阈值的正交距离,结束。
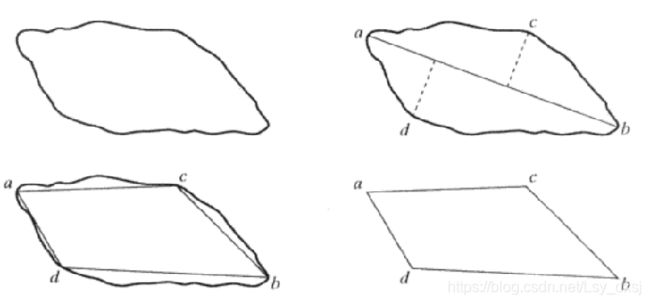
以下是实验内容:


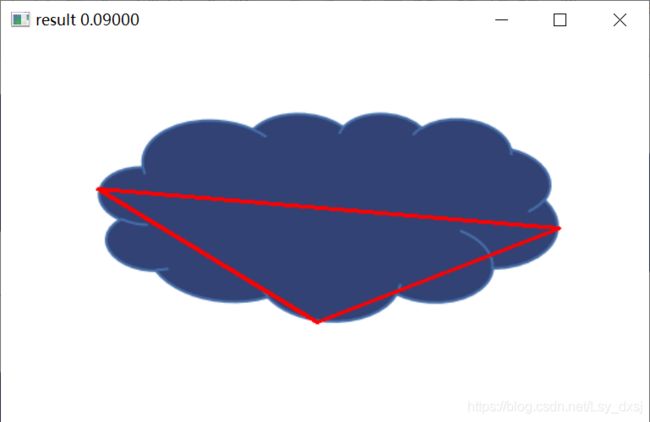

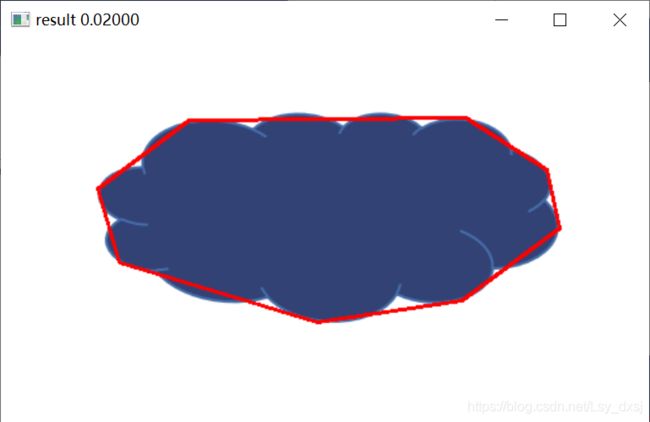

随着逼近多边形尺度的缩小,越来越贴近给定边界的基本形状。
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def get_approx(img, contour, length_p=0.1):
img_adp = img.copy()
# 逼近长度计算
epsilon = length_p * cv2.arcLength(contour, True)
# 获取逼近多边形
approx = cv2.approxPolyDP(contour, epsilon, True)
# 绘制显示多边形
cv2.drawContours(img_adp, [approx], 0, (0, 0, 255), 2)
cv2.imshow("result %.5f" % length_p, img_adp)
def main():
# 1.导入图片, 显示原始图片
img_src = cv2.imread('C:/Users/13121/Desktop/18.png')
cv2.imshow("img_src", img_src)
# 2.灰度化,二值化
img_gray = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
ret, img_bin = cv2.threshold(img_gray, 127, 255, cv2.THRESH_BINARY)
# 3.连通域分析
contours, hierarchy = cv2.findContours(img_bin,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
# 4.获取不同尺度的逼近多边形
get_approx(img_src, contours[0], 0.15)
get_approx(img_src, contours[0], 0.09)
get_approx(img_src, contours[0], 0.05)
get_approx(img_src, contours[0], 0.02)
get_approx(img_src, contours[0], 0.002)
cv2.waitKey()
cv2.destroyAllWindows()
if __name__ == '__main__':
main()
4. 标记图
标记图是边界的一维函数表示,可以使用各种方式生成,最简单的方法是:角度的函数的形式画出质心到边界的距离。
标记图可以以角度的函数的形式画出质心到边界的距离,这种方法所生成的标记图平移不变,旋转和缩放会变。
| 问题 | 方法 |
|---|---|
| 旋转变换使得标记图改变 | a. 选取相同起始点生成标记图实现旋转归一化 b. 在本征轴上选取距质心最远的点 c. 使用一阶差分的链码 |
| 缩放变换使得标记图改变 | a. 对所有函数进行缩放,使它们有相同的值域 b. 将每个样本除以标记图的方差 |
无论使用哪种方法,基本思想都是消除对尺寸的依赖性,同时保持波形的基本形状。
5. 边界线段
将边界分解为线段可降低边界的复杂性,简化描述过程。
定义:一个任意集合S的凸壳H是包含S的最小凸集,集合之差H-S称为集合S的凸缺D。
方案:追踪S的轮廓,并标记进入或离开一个凸缺的转变点。
在原理上,这种方案与区域大小和方向无关。

但由于图像会受到噪声的影响,易产生一些随机散布的无意义的凸缺,因此在用边界线段进行边界分割前,先要平滑边界,方法有两种:
(1)追踪边界,并使用一个像素沿该边界的k个相邻像素的平均坐标代替这个像素的坐标
(2)在找到一个区域的凸缺前,先使用多边形近似
6. 骨架
骨架是区域表示方法,通过把平面区域抽取为图来表示边界。
思想:表示一个平面区域结构形状的重要方法是把它削减成图形,这种削减可以通过细化(也称为抽骨架)算法,获取区域的骨架来实现。
例如:中轴变换(MAT)细化算法。
三、边界描绘子
主要借助区域的外部特征即区域的边界来描述区域。
1. 一些简单的描绘子
| 一些简单的描绘子 | 定义 |
|---|---|
| 边界的长度 | 一条边界上的像素数量可给出其长度的粗略近似 |
| 边界的直径 | D i a m ( B ) = m a x i , j [ D ( p i , p j ) ] Diam(B)=max_{i,j}[D(p_i,p_j)] Diam(B)=maxi,j[D(pi,pj)],D是欧氏距离或几何距离,pi,pj是边界上的点 |
| 偏心率 | 直径的值和连接组成该直径的两个端点的直线段为边界的长轴,与长轴垂直的直线短为短轴,长轴与短轴之比为边界的偏心率 |
| 曲率 | 斜率的变化率,有时也使用相邻边界线段的斜率差作为这两条线段交点处曲率的描绘子 |
| 凸线段 | 当顶点p处的斜率变化非负时,称之为凸线段上的点 |
| 凹线段 | 当顶点p处的斜率变化为负时,称之为凹线段上的点 |
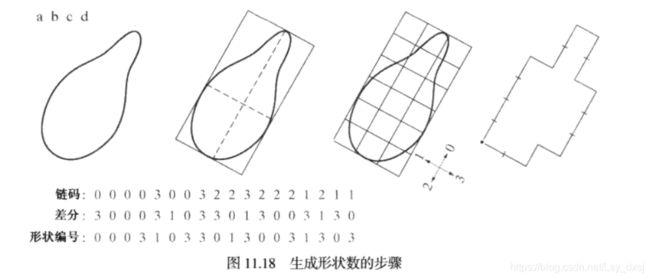
2. 形状数
是基于4-链码的边界描述符,为值最小的4-链码的一阶差分码
形状树与方向无关,虽然链码的首差不依赖于旋转,但一般情况下边界的编码依赖于网格的方向,所以在边界描述之前,需要规整化网格方向。
规整化网格方向的一种算法如下:
(1)首先确定形状数的序号 n;
(2)在序号为 n 的矩形形状数中,找出一个与给定形状的基本矩形的离心率最接近的形状数;
(3)然后再用这个矩形与基本矩形对齐,构造网格;
(4)用获得链码的方法得到链码;
(5)再得到循环首差;
(6)首差中的最小循环数即为形状数。
3. 傅里叶描绘子
对于边界的点坐标可以表示为s(k)=[x(k),y(k)],x(k)=xk,y(k)=yk,用复数表示为:
s ( k ) = x ( k ) + j y ( k ) s(k)=x(k)+jy(k) s(k)=x(k)+jy(k)
也就是说,x轴为复数序列的实轴,y轴为复数序列的虚轴。
s(k)的离散傅里叶变换为:
a ( u ) = Σ k = 0 K − 1 s ( k ) e − j 2 π u k K a(u)=\Sigma_{k=0}^{K-1}s(k)e^{\frac{-j2\pi uk}{K}} a(u)=Σk=0K−1s(k)eK−j2πuk
a(u)是边界的傅里叶描绘子。
s ( k ) = 1 K Σ u = 0 P − 1 a ( u ) e j 2 π u k P s(k)=\frac{1}{K}\Sigma_{u=0}^{P-1}a(u)e^{\frac{j2\pi uk}{P}} s(k)=K1Σu=0P−1a(u)ePj2πuk

4. 统计矩
边界线段的形状可使用统计矩来定量描述,如均值、方差和高阶矩。
矩 为 : μ n ( r ) = ∑ i = 0 K − 1 ( r i − m ) n g ( r i ) 矩为:\begin{array}{c} \mu_{n}(r)=\sum_{i=0}^{K-1}\left(r_{i}-m\right)^{n} g\left(r_{i}\right) \\ \end{array} 矩为:μn(r)=∑i=0K−1(ri−m)ng(ri)
其 中 , m = ∑ i = 0 K − 1 r i g ( r i ) 其中,m=\sum_{i=0}^{K-1} r_{i} g\left(r_{i}\right) 其中,m=i=0∑K−1rig(ri)
低阶矩描述图像的整体特征,高阶矩描述图像的细节。
四、区域描绘子
1. 一些简单的描绘子
| 一些简单的区域描绘子 | 定义 |
|---|---|
| 面积 | 一个区域的面积定义为该区域中像素的数量 |
| 周长 | 区域的周长是其边界的长度 |
| 圆周率 | 一个区域的面积与具有相同周长的一个圆(最致密的形状)的面积之比 |
用作区域描绘子的其他简单度量包括灰度级的均值和中值、最小灰度值和最大灰度值,以及其值高于和低于均值的像素数。
2. 拓扑描绘子
拓扑特性对图像平面区域的整体描述很有用,它与距离或基于距离度量概念的任何特性无关。主要用于研究一种图像在没有撕裂和连接的情况下(橡皮伸展变形),不受任何变形影响的性质。
区域内的孔洞数量和连通分量的数量对区域描述很有用。若图中孔洞的数量为H,连通分量数量为C,则可用于定义欧拉数E, E = C − H E=C-H E=C−H
若顶点数为V,边数为Q,面数为F ,则可得出欧拉公式 V − Q + F = C − H = E V-Q+F=C-H=E V−Q+F=C−H=E
3. 纹理
反映像素灰度的空间分布属性的图像特征。
图像处理中用于描述区域纹理的三种主要方法是统计方法、结构方法和频谱方法。
| 描述区域纹理的方法 | 应用场景 |
|---|---|
| 统计方法 | 生成诸如平滑、粗糙、粒状的等纹理特征 |
| 结构方法 | 处理图像像元的排列 |
| 频谱方法 | 检测图像中的全局周期性 |
4. 不变矩
不变矩表征了图像区域的几何特征,且其具有旋转、平移、尺度变化、镜像(内部为负号)等特性的不变特征。在图像处理中,几何不变矩作为一个重要的特征来表示物体。
五、使用主分量进行描绘
总体向量均值: m x = E { x } m_{\mathrm{x}}=E\{x\} mx=E{x}
总体向量协方差矩阵: C x = E { ( x − m x ) ( x − m x ) T } \boldsymbol{C}_{\mathbf{x}}=E\left\{\left(\boldsymbol{x}-\boldsymbol{m}_{x}\right)\left(\boldsymbol{x}-\boldsymbol{m}_{x}\right)^{\mathrm{T}}\right\} Cx=E{(x−mx)(x−mx)T}
样本均值: m x = 1 K ∑ k = 1 K m x m_{x}=\frac{1}{K} \sum_{k=1}^{K} m_{x} mx=K1∑k=1Kmx
样本协方差矩阵: C x = 1 K ∑ k = 1 K x k x k T − m x m x T \boldsymbol{C}_{\boldsymbol{x}}=\frac{1}{K} \sum_{k=1}^{K} \boldsymbol{x}_{k} \boldsymbol{x}_{k}^{\mathrm{T}}-\boldsymbol{m}_{x} \boldsymbol{m}_{x}^{\mathrm{T}} Cx=K1∑k=1KxkxkT−mxmxT
主要是通过以上四个概念来求一个变换矩阵——霍特林变换(也就是主分量变换)
霍特林变换表达式:
y = A ( x − m x ) y=A( x-m_x) y=A(x−mx)
使用主分量描述图像
由对应最大特征值的向量分量形成的图像会显示最高的对比度。
用主分量对尺度、平移和旋转变化归一化
为将所有坐标转换为正值,可从所有y向量中减去(y1min,y2min)T
为置换结果点使它们都大于零,对所有点加上向量(a,b)T,其中a和b都大于0
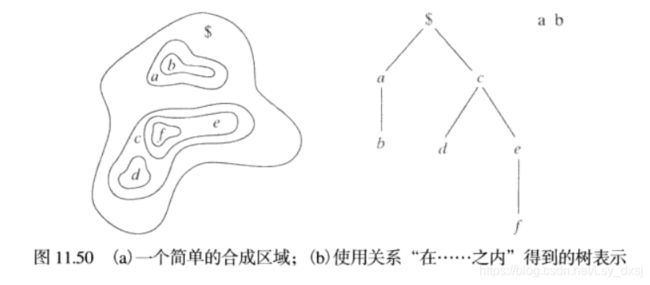
六、关系描绘子
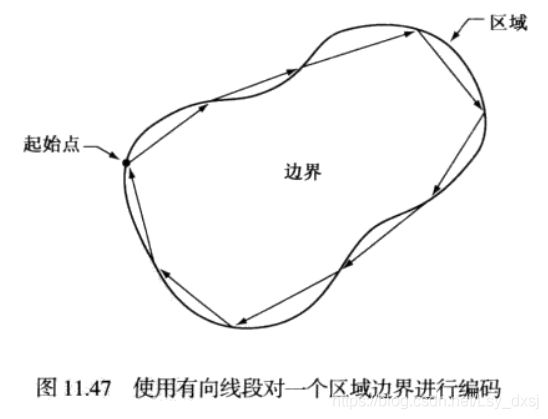
关系描绘子对边界和区域都适用,主要以重写规则的形式来获取边界或区域中的基本重复模式。大多数使用字符串来描述图像的应用均基于从感兴趣的物体中提取连接线段的思想。
一种方法是追踪一个物体的轮廓,并使用指定方向和/或长度的线段来对结果进行编码;
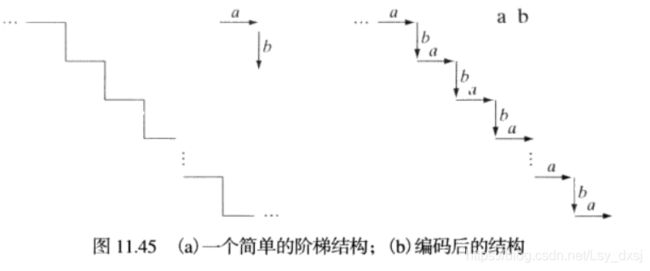
使用有向线段来描述图像的各个部分(如较小的单色区域)
根据抽象的基元来定义典型的操作,比如有时有着类似纹理或其他描绘子的区域可能是不连续的,这种情况下可以使用树描绘子。