VDSR论文学习笔记

       VDSR网络是韩国首尔国立大学Jiwon Kim等人在SRCNN基础上又一次新的突破，在单图像超分辨率重建（SR）方面展示出了更好的性能。

针对SRCNN存在的三个局限性：

①依赖于小图像区域的Context；

②收敛速度较慢；

③网络只适用于单一规模。

VDSR的主要改进：

①使用非常大的感受野（41×41）和非常深的网络（20层），以适应非常大的图像区域上的上下文信息；

②残差学习和梯度裁剪，学习LR到HR图像的残差以加快收敛速度，同时使用较高的学习率（SRCNN的倍）；

③提出单模型SR方法以减少参数，在单个模型中实现任意比例因子，且可以为分数，实现多尺度SR；

④与SRCNN不同之处还有：VDSR网络输入输出图像大小相同，SRCNN输出图片尺寸小于输入；VDSR网络的所有层使用相同的学习速率，而SRCNN对不同层使用不同的学习速率以实现稳定的收敛。

VDSR网络结构：

        该网络共D个卷积层，卷积核大小均为64×3×3，其中第一层对输入图像进行操作，最后一层用于图像重建，使用单个滤波器，其余层均使用64个滤波器。网络将插值的低分辨率图像（达到所目标尺寸）作为输入，并预测图像细节，y(HR)=x(Residual)+r(LR)，网络的每层均使用padding以保证输入输出图像尺寸一致。

损失函数：（其中r=HR-LR，f(x)表示网络的预测值）

       在训练中，为了最大收敛速度，该网络将梯度剪裁为，其中表示当前学习率，表示预定义的范围。为了训练了多尺度模型，将几个特定尺度的训练数据集组合成一个大数据集。数据准备与SRCNN相似，但在此输入patches大小等于感受野的大小，图像被分割成没有重叠的子图像。一个mini-batch由64个子图像组成，其中不同比例的子图像可以在同一个batch中。

训练数据集：91-images（Banchmark使用291-images）

测试数据集：Set5、Set14、Urban100、B100

数据处理：与SRCNN类似，将原始图像划分为×（1000张1×41×41）的子图像块，但彼此间没有重叠部分，每个batch包括64张子图像，同时将不同比例因子的图像合成一个大数据集用于多尺度训练。

网络结构的pytorch实现：

class Conv_ReLU_Block(nn.Module):
    def __init__(self):
        super(Conv_ReLU_Block, self).__init__()
        self.conv = nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, stride=1, padding=1, bias=False)
        self.relu = nn.ReLU(inplace=True)
        
    def forward(self, x):
        return self.relu(self.conv(x))

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.residual_layer = self.make_layer(Conv_ReLU_Block, 18)
        self.input = nn.Conv2d(in_channels=1, out_channels=64, kernel_size=3, stride=1, padding=1, bias=False)
        self.output = nn.Conv2d(in_channels=64, out_channels=1, kernel_size=3, stride=1, padding=1, bias=False)
        self.relu = nn.ReLU(inplace=True)

        # 权值参数初始化
        print(self.modules())
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, sqrt(2. / n))  # m.weight.data是卷积核参数, m.bias.data是偏置项参数
                
    def make_layer(self, block, num_of_layer):
        layers = []
        for _ in range(num_of_layer):
            layers.append(block())
        print(nn.Sequential(*layers))
        return nn.Sequential(*layers)

    def forward(self, x):
        residual = x
        out = self.relu(self.input(x))
        out = self.residual_layer(out)
        out = self.output(out)
        out = torch.add(out,residual)
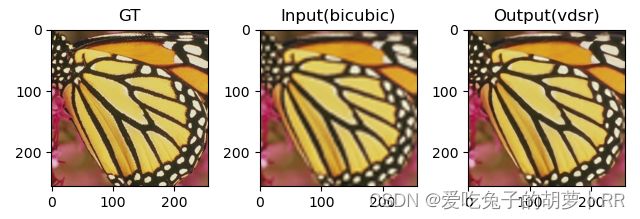
        return out

重建效果：

PS：

感受野大小 ：

       对于N个卷积核为n的滤波器组成的网络，第一层感受野为n×n，第D层的感受野为（(N-1)D+1）×（(N-1)D+1），感受野的大小与网络深度成正比。此时一个大的滤波器就可以有效地分解为一系列小的滤波器，从而加深了网络。在SR任务中，较大的感受野意味着网络可以使用更多的上下文来预测图像细节。

梯度裁剪：

       如果梯度值小于负阈值或大于正阈值，则梯度值裁剪将损失函数的导数剪切为给定值。例如，可以将范数指定为0.5，这意味着如果梯度值小于-0.5，则将其设置为-0.5，如果梯度值大于0.5，则将其设置为0.5。

pytorch中梯度剪裁方法：torch.nn.utils.clip_grad_norm_(parameters, max_norm, norm_type=2)

parameters：希望实施梯度裁剪的可迭代网络参数
max_norm：该组网络参数梯度的范数上限
norm_type：范数类型，默认为L2

He初始化：

       He初始化是何凯明等提出的一种鲁棒的神经网络参数初始化方法，为了保证信息在前向传播和反向传播过程中能够有效流动，使不同层的输入信号的方差大致相等。其对应的是非线性激活函数（Relu 和 Prelu）。

结论：各层权重初始化为期望为0，标准差为的高斯分布，并且将b初始化为0。用公式表示为：

其中表示第L层的神经元个数。

Pytorch代码实现：

# 权值参数初始化
for m in self.modules():
    if isinstance(m, nn.Conv2d):
        n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
        m.weight.data.normal_(0, sqrt(2. / n))  # m.weight.data是卷积核参数, m.bias.data是偏置项参数