opencv 插值方式

一、插值方式与resize()的关系

resize()函数里面包含插值的几种方式：

void resize(InputArray src,//输入，原图像，即待改变大小的图像；
 OutputArray dst,  //输出，改变大小之后的图像，这个图像和原图像具有相同的内容，只是大小和原图像不一样而已；
 Size dsize,  //输出图像的大小。如果这个参数不为0，那么就代表将原图像缩放到这个Size(width，height)指定的大小；如果这个参数为0，那么原图像缩放之后的大小就要通过下面的公式来计算：
 double fx=0, // width方向的缩放比例，如果它是0，那么它就会按照(double)dsize.width/src.cols来计算；
 double fy=0, //height方向的缩放比例，如果它是0，那么它就会按照(double)dsize.height/src.rows来计算；
 int interpolation=INTER_LINEAR// 这个是指定插值的方式，图像缩放之后，肯定像素要进行重新计算的，就靠这个参数来指定重新计算像素的方式，有以下几种：
      INTER_NEAREST - 最邻近插值
      INTER_LINEAR - 双线性插值，如果最后一个参数你不指定，默认使用这种方法
      INTER_AREA -区域插值 resampling using pixel area relation. It may be a preferred method for image decimation, as it gives moire’-free results. But when the image is zoomed, it is similar to the INTER_NEAREST method.
      INTER_CUBIC - 4x4像素邻域内的双立方插值
      INTER_LANCZOS4 - 8x8像素邻域内的Lanczos插值
 );
 使用注意事项：
   dsize和fx/fy不能同时为0，

 ​

 

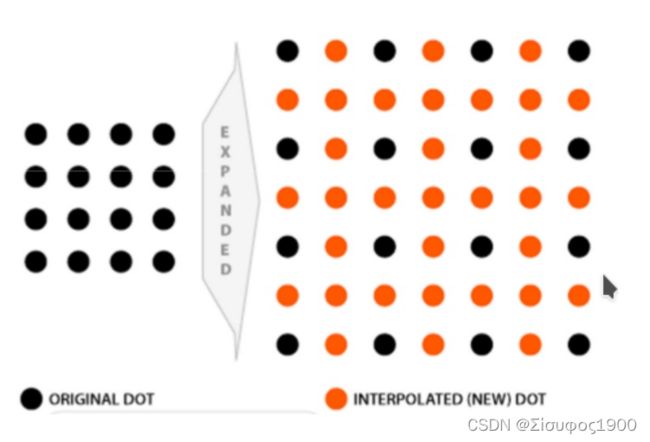
二、近邻插值INTER_NEAREST

最近邻插值法， 找到与之距离最相近的邻居（原来就存在的像素点， 黑点）， 赋值与其相同。

实现opencv中常用的三种插值算法 - 简书 

​

 

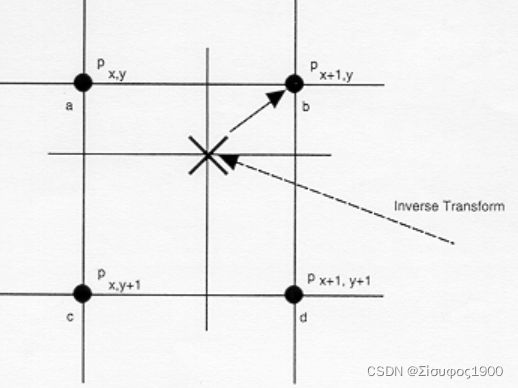
//最近邻域插值
//根据目标图像的像素点（浮点坐标）找到原始图像中的4个像素点，取距离该像素点最近的一个原始像素值作为该点的值。

#include
#include

namespace mycv {
    void nearestIntertoplation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols);
}//mycv

double distance(const double x1, const double y1, const double x2, const double y2);//两点之间距离，这里用欧式距离

int main()
{
    cv::Mat img = cv::imread("lena.jpg", 0);
    if (img.empty()) return -1;
    cv::Mat dst;
    mycv::nearestIntertoplation(img, dst, 600, 600);
    cv::imshow("img", img);
    cv::imshow("dst", dst);
    cv::waitKey(0);
    return 0;
    return 0;
}//main

void mycv::nearestIntertoplation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
    //比例尺
    const double scale_row = static_cast<double>(src.rows) / rows;
    const double scale_col = static_cast<double>(src.rows) / cols;

    //扩展src到dst
    dst = cv::Mat(rows, cols, src.type());
    assert(src.channels() == 1 && dst.channels() == 1);

    for (int i = 0; i < rows; ++i)//dst的行
        for (int j = 0; j < cols; ++j)//dst的列
        {
            //求插值的四个点
            double y = (i + 0.5) * scale_row + 0.5;
            double x = (j + 0.5) * scale_col + 0.5;
            int x1 = static_cast<int>(x);//col对应x
            if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
            int x2 = x1 + 1;
            int y1 = static_cast<int>(y);//row对应y
            if (y1 >= (src.rows - 2))  y1 = src.rows - 2;
            int y2 = y1 + 1;
            //根据目标图像的像素点（浮点坐标）找到原始图像中的4个像素点，取距离该像素点最近的一个原始像素值作为该点的值。
            assert(0 < x2 && x2 < src.cols && 0 < y2 &&  y2 < src.rows);
            std::vector<double> dist(4);
            dist[0] = distance(x, y, x1, y1);
            dist[1] = distance(x, y, x2, y1);
            dist[2] = distance(x, y, x1, y2);
            dist[3] = distance(x, y, x2, y2);

            int min_val = dist[0];
            int min_index = 0;
            for (int i = 1; i < dist.size(); ++i)
                if (min_val > dist[i])
                {
                    min_val = dist[i];
                    min_index = i;
                }

            switch (min_index)
            {
            case 0:
                dst.at(i, j) = src.at(y1, x1);
                break;
            case 1:
                dst.at(i, j) = src.at(y1, x2);
                break;
            case 2:
                dst.at(i, j) = src.at(y2, x1);
                break;
            case 3:
                dst.at(i, j) = src.at(y2, x2);
                break;
            default:
                assert(false);
            }           
        }
}

double distance(const double x1, const double y1, const double x2, const double y2)//两点之间距离，这里用欧式距离
{
    return (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);//只需比较大小，返回距离平方即可
}

 三、线性插值

已知两点（红色） ，在给出一个蓝点的x坐标， 求y。

 

//线性内插（双线性插值)
#include
#include
#include

namespace mycv {
    void bilinearIntertpolatioin(cv::Mat& src, cv::Mat& dst, const int rows, const int cols);
}//mycv

int main()
{
    cv::Mat img = cv::imread("lena.jpg", 0);
    if (img.empty()) return -1;
    cv::Mat dst;
    mycv::bilinearIntertpolatioin(img, dst, 600, 600);
    cv::imshow("img", img);
    cv::imshow("dst", dst);
    cv::waitKey(0);
    return 0;
}//main

void mycv::bilinearIntertpolatioin(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
    //比例尺
    const double scale_row = static_cast<double>(src.rows) / rows;
    const double scale_col = static_cast<double>(src.rows) / cols;

    //扩展src到dst
    dst = cv::Mat(rows, cols, src.type());
    assert(src.channels() == 1 && dst.channels() == 1);
    
    for(int i = 0; i < rows; ++i)//dst的行
        for (int j = 0; j < cols; ++j)//dst的列
        {
            //求插值的四个点
            double y = (i + 0.5) * scale_row + 0.5;
            double x = (j + 0.5) * scale_col + 0.5;
            int x1 = static_cast<int>(x);//col对应x
            if (x1 >= (src.cols - 2)) x1 = src.cols - 2;//防止越界
            int x2 = x1 + 1;
            int y1 = static_cast<int>(y);//row对应y
            if (y1 >= (src.rows - 2))  y1 = src.rows - 2;
            int y2 = y1 + 1;

            assert(0 < x2 && x2 < src.cols && 0 < y2 &&  y2 < src.rows);
            //插值公式,参考维基百科矩阵相乘的公式https://zh.wikipedia.org/wiki/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC
    
            cv::Matx12d matx = { x2 - x, x - x1 };
            cv::Matx22d matf = { static_cast<double>(src.at(y1, x1)), static_cast<double>(src.at(y2, x1)),
                                 static_cast<double>(src.at(y1, x2)), static_cast<double>(src.at(y2, x2)) };
            cv::Matx21d maty = {
                y2 - y,
                y - y1
            };

            auto  val = (matx * matf * maty);
            dst.at(i, j) = val(0,0);
        }

}

四、双三次插值

在数值分析这个数学分支中，双三次插值（英语：Bicubic interpolation）是二维空间中最常用的插值方法。在这种方法中，函数 f 在点 (x, y) 的值可以通过矩形网格中最近的十六个采样点的加权平均得到，在这里需要使用两个多项式插值三次函数，每个方向使用一个

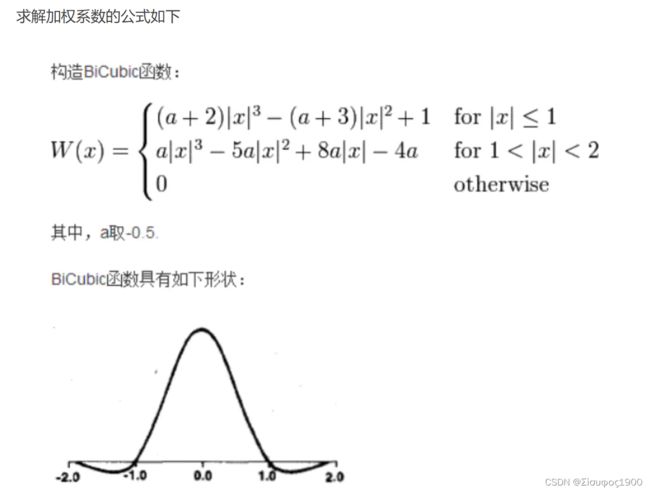
双三次插值计算公式​
 

​ 

 

那么这个a(i, j)便是介绍里面所说的加权系数了，所以关键是要把它求解出来。

求解加权系数的公式如下​

 

求解加强系数代码如下：

std::vector mycv::getW(double coor, double a)
{
    std::vector w(4);
    int base = static_cast(coor);//取整作为基准
    double e = coor - static_cast(base);//多出基准的小数部分
    std::vector tmp(4);//存放公式中 |x| <= 1,  1 < |x| < 2四个值
    // 4 x 4的16个点，所以tmp[0]和tmp[4]距离较远，值在[1, 2]区间
    tmp[0] = 1.0 + e;// 1 < x < 2
    tmp[1] = e;//x <= 1
    tmp[2] = 1.0 - e;// x <= 1
    tmp[3] = 2.0 - e;// 1 < x < 2

    //按照bicubic公式计算系数w
    // x <= 1
    w[1] = (a + 2.0) * std::abs(std::pow(tmp[1], 3)) - (a + 3.0) * std::abs(std::pow(tmp[1], 2)) + 1;
    w[2] = (a + 2.0) * std::abs(std::pow(tmp[2], 3)) - (a + 3.0) * std::abs(std::pow(tmp[2], 2)) + 1;
    // 1 < x < 2
    w[0] = a * std::abs(std::pow(tmp[0], 3)) - 5.0 * a * std::abs(std::pow(tmp[0], 2)) + 8.0*a*std::abs(tmp[0]) - 4.0*a;
    w[3] = a * std::abs(std::pow(tmp[3], 3)) - 5.0 * a * std::abs(std::pow(tmp[3], 2)) + 8.0*a*std::abs(tmp[3]) - 4.0*a;

    return w;
}

求解出来之后，wx和wy就是4x4组成的16个系数，与插值所需要用到4x4的16个点相匹配。插值步骤的关键代码

                //4x4数量的点(rr, cc) -> (y, x)
                std::vector > src_arr = {
                    { src.at(rr - 1, cc - 1), src.at(rr, cc - 1), src.at(rr + 1, cc - 1), src.at(rr + 2, cc - 1)},
                    { src.at(rr - 1, cc), src.at(rr, cc), src.at(rr + 1, cc), src.at(rr + 2, cc)},
                    { src.at(rr - 1, cc + 1), src.at(rr, cc + 1), src.at(rr + 1, cc + 1), src.at(rr + 2, cc + 1)},
                    { src.at(rr - 1, cc + 2), src.at(rr, cc + 2), src.at(rr + 1, cc + 2), src.at(rr + 2, cc + 2)}
                };
                for(int p = 0; p < 3; ++p)
                    for (int q = 0; q < 3; ++q)
                    {
                        //val(p, q) = w(p,q) * src(p, q)
                        val += wr[p] * wc[q] * static_cast(src_arr[p][q]);
                    }
                assert(i < dst.rows && j < dst.cols);
                dst.at(i, j) = static_cast(val);















//双三次插值

#include
#include
#include
#include

namespace mycv {
    void bicubicInsterpolation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols);
    std::vector getW(double coor, double a = -0.5);//a默认-0.5
}//mycv

int main(void)
{
    cv::Mat img = cv::imread("lena.jpg", 0);
    if (img.empty()) return -1;
    cv::Mat dst;
    mycv::bicubicInsterpolation(img, dst, 600, 600);
    cv::imshow("img", img);
    cv::imshow("dst", dst);
    cv::waitKey(0);
    return 0;
}//main

void mycv::bicubicInsterpolation(cv::Mat& src, cv::Mat& dst, const int rows, const int cols)
{
    dst = cv::Mat(rows, cols, src.type(), cv::Scalar::all(0));//初始化dst
    //比例尺
    double row_scale = static_cast(src.rows) / rows;
    double col_scale = static_cast(src.cols) / cols;

    switch (src.channels())
    {

    case 1://灰度
        for(int i = 2; i < dst.rows - 2; ++i)
            for (int j = 2; j < dst.cols - 2; ++j)
            {
                //计算系数w
                double r = static_cast(i *  row_scale);
                double c = static_cast(j *  col_scale);
                
                //防止越界
                if (r < 1.0) r += 1.0;
                if (c < 1.0) c += 1.0;
            

                std::vector wr = mycv::getW( r);
                std::vector wc = mycv::getW( c);
                
                //最后计算插值得到的灰度值
                double val = 0;
                int cc = static_cast(c);
                int rr = static_cast(r);
                //防止越界
                if (cc > src.cols - 3)
                {
                    cc = src.cols - 3;
                    
                }
                if (rr > src.rows - 3) rr = src.rows - 3;

                assert(0 <= (rr - 1) && 0 <= (cc - 1) && (rr + 2) < src.rows && (cc + 2) < src.cols);

                //4x4数量的点(rr, cc) -> (y, x)
                std::vector > src_arr = {
                    { src.at(rr - 1, cc - 1), src.at(rr, cc - 1), src.at(rr + 1, cc - 1), src.at(rr + 2, cc - 1)},
                    { src.at(rr - 1, cc), src.at(rr, cc), src.at(rr + 1, cc), src.at(rr + 2, cc)},
                    { src.at(rr - 1, cc + 1), src.at(rr, cc + 1), src.at(rr + 1, cc + 1), src.at(rr + 2, cc + 1)},
                    { src.at(rr - 1, cc + 2), src.at(rr, cc + 2), src.at(rr + 1, cc + 2), src.at(rr + 2, cc + 2)}
                };
                for(int p = 0; p < 3; ++p)
                    for (int q = 0; q < 3; ++q)
                    {
                        //val(p, q) = w(p,q) * src(p, q)
                        val += wr[p] * wc[q] * static_cast(src_arr[p][q]);
                    }
                assert(i < dst.rows && j < dst.cols);
                dst.at(i, j) = static_cast(val);
                
            }
        break;
    case 3://彩色(原理一样多了两个通道而已)
        break;
    default:
        break;
    }
}

std::vector mycv::getW(double coor, double a)
{
    std::vector w(4);
    int base = static_cast(coor);//取整作为基准
    double e = coor - static_cast(base);//多出基准的小数部分
    std::vector tmp(4);//存放公式中 |x| <= 1,  1 < |x| < 2四个值
    // 4 x 4的16个点，所以tmp[0]和tmp[4]距离较远，值在[1, 2]区间
    tmp[0] = 1.0 + e;// 1 < x < 2
    tmp[1] = e;//x <= 1
    tmp[2] = 1.0 - e;// x <= 1
    tmp[3] = 2.0 - e;// 1 < x < 2

    //按照bicubic公式计算系数w
    // x <= 1
    w[1] = (a + 2.0) * std::abs(std::pow(tmp[1], 3)) - (a + 3.0) * std::abs(std::pow(tmp[1], 2)) + 1;
    w[2] = (a + 2.0) * std::abs(std::pow(tmp[2], 3)) - (a + 3.0) * std::abs(std::pow(tmp[2], 2)) + 1;
    // 1 < x < 2
    w[0] = a * std::abs(std::pow(tmp[0], 3)) - 5.0 * a * std::abs(std::pow(tmp[0], 2)) + 8.0*a*std::abs(tmp[0]) - 4.0*a;
    w[3] = a * std::abs(std::pow(tmp[3], 3)) - 5.0 * a * std::abs(std::pow(tmp[3], 2)) + 8.0*a*std::abs(tmp[3]) - 4.0*a;

    return w;
}