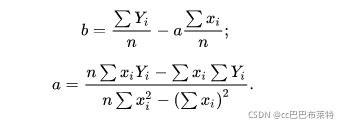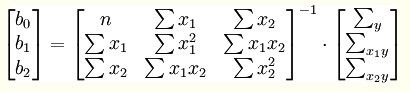多元线性回归算法预测房价

目录

一、线性回归理论基础

二、多元线性回归

1、针对房屋数据集“house_prices.csv”做多元线性回归（基于统计分析库statsmodels）

三、用Excel重做上面的多元线性回归，求解回归方程

四、用机器学习库Sklearn库重做上面的多元线性回归

五、三者的结果对比分析

六、总结

---

        garbage in garbage out”（简称GIGO），是计算机术语常用的俚语，意思是如果你输入错误的数据，那么（计算机）输出的结果也是错误的。这个结论在机器学习领域也成立。多元线性回归属于监督机器学习算法，通过已知数据训练得到模型或决策函数。应用此算法时，不能盲目地套用算法，必须对数据的有效性、正确性、假设合理性进行验证，如果发现数据本身不正确，就需要纠正。多元线性回归适用于对受到多因素影响的数据进行分析的场景。由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。

一、线性回归理论基础

        一元线性回归分析是只有一个自变量（自变量x和因变量y）线性相关关系的方法。一个经济指标的数值往往受许多因素影响，若其中只有一个因素是主要的，起决定性作用，则可用一元线性回归进行预测分析。一元线性回归分析的数学模型为：

        其中，是自变量的值；

        是因变量的值；

        a、b是代表一元线性回归方程的参数。

        a、b参数由下列公式可求得：

        多元线性回归分析中的因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。设为因变量，为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

        其中，为常数项，为回归系数，为固定时，每增加一个单位对的效应，即对的偏回归系数；同理，为固定时，每增加一个单位对的效应，即对的偏回归系数 ，等等。如果两个自变量、同一个因变量呈线性相关时，可用二元线性回归模型描述为：

         建立多元线性回归模型时，为了保证回归模型具有优良的解释能力和预测效果，应首先注意自变量的选择，其准则是：

(1)自变量对因变量必须有显著的影响，并呈密切的线性相关；

(2)自变量与因变量之间的线性相关必须是真实的，而不是形式上的；

(3)自变量之间应具有一定的互斥性，即自变量之间的相关程度不应高于自变量与因变量之间的相关程度；

(4)自变量应具有完整的统计数据，其预测值容易确定。

        多元线性回归模型的参数统计，同一元线性回归方程的一样，也是在要求误差平方和为最小的前提下，用最小二乘法求解参数。以二元线性回归模型为例，求解回归方程参数的标准方程组为：

 解此方程可求得的值，亦可以通过下列矩阵法求得：

 回归性能好坏使用均方误差(Mean Squared Error)MSE进行评估，评估机制：

其中，为预测值，为真实值。

二、多元线性回归

1、针对房屋数据集“house_prices.csv”做多元线性回归（基于统计分析库statsmodels）

1）基础包导入

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

2）读取文件house_prices.csv中的数据

df = pd.read_csv('house_prices.csv')
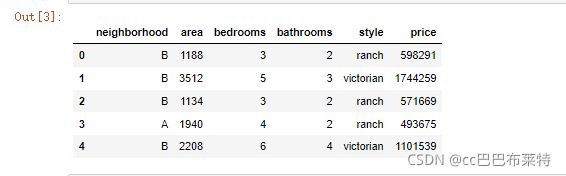
df.info(); df.head()

读取结果输出：

3）数据处理，对异常值进行检测

# 异常值处理
# ================ 异常值检验函数：iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
    """ 以某列为依据，使用 上下截断点法 检测异常值(索引) """
    """ 
    full_data: 完整数据
    column: full_data 中的指定行，格式 'x' 带引号
    return 可选; outlier: 异常值数据框 
    upper: 上截断点;  lower: 下截断点
    method：检验异常值的方法（可选, 默认的 None 为上下截断点法），
            选 Z 方法时，Z 默认为 2
    """
    # ================== 上下截断点法检验异常值 ==============================
    if method == None:
        print(f'以 {column} 列为依据，使用 上下截断点法(iqr) 检测异常值...')
        print('=' * 70)
        # 四分位点；这里调用函数会存在异常
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1，3 分位数
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # 计算上下截断点
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'第一分位数: {q1}, 第三分位数：{q3}, 四分位极差：{column_iqr}')
        print(f"上截断点：{upper}, 下截断点：{lower}")
        return outlier, upper, lower
    # ===================== Z 分数检验异常值 ==========================
    if method == 'z':
        """ 以某列为依据，传入数据与希望分段的 z 分数点，返回异常值索引与所在数据框 """
        """ 
        params
        data: 完整数据
        column: 指定的检测列
        z: Z分位数, 默认为2，根据 z分数-正态曲线表，可知取左右两端的 2%，
           根据您 z 分数的正负设置。也可以任意更改，知道任意顶端百分比的数据集合
        """
        print(f'以 {column} 列为依据，使用 Z 分数法，z 分位数取 {z} 来检测异常值...')
        print('=' * 70)
        # 计算两个 Z 分数的数值点
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"取 {z} 个 Z分数：大于 {upper} 或小于 {lower} 的即可被视为异常值。")
        print('=' * 70)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

注意：如果确定了是用 z-score 或者 iqr 法，注意只是处理一次即可。只要是再次检测，就又会有 “ 新的 ” 异常值出现，因为 z-score/iqr 的计算公式会根据第一次处理后的新的样本集来弄。

4）调用函数

outlier, upper, lower = outlier_test(data=df, column='price', method='z')
outlier.info(); outlier.sample(5)

 5）丢弃错误数据即异常值

# 这里简单的丢弃即可
df.drop(index=outlier.index, inplace=True)

6）定义变量

# 类别变量，又称为名义变量，nominal variables
nominal_vars = ['neighborhood', 'style']

for each in nominal_vars:
    print(each, ':')
    print(df[each].agg(['value_counts']).T)
    # 直接 .value_counts().T 无法实现下面的效果
     ## 必须得 agg，而且里面的中括号 [] 也不能少
    print('='*35)
    # 发现各类别的数量也都还可以，为下面的方差分析做准备

7）定义热力图函数，查看变量相关性

# 热力图 
def heatmap(data, method='pearson', camp='RdYlGn', figsize=(10 ,8)):
    """
    data: 整份数据
    method：默认为 pearson 系数
    camp：默认为：RdYlGn-红黄蓝；YlGnBu-黄绿蓝；Blues/Greens 也是不错的选择
    figsize: 默认为 10，8
    """
    ## 消除斜对角颜色重复的色块
    #     mask = np.zeros_like(df2.corr())
    #     mask[np.tril_indices_from(mask)] = True
    plt.figure(figsize=figsize, dpi= 80)
    sns.heatmap(data.corr(method=method), \
                xticklabels=data.corr(method=method).columns, \
                yticklabels=data.corr(method=method).columns, cmap=camp, \
                center=0, annot=True)
    # 要想实现只是留下对角线一半的效果，括号内的参数可以加上 mask=mask

8）调用函数输出结果

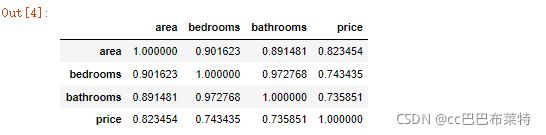
# 通过热力图可以看出 area，bedrooms，bathrooms 等变量与房屋价格 price 的关系都还比较强
 ## 所以值得放入模型，但分类变量 style 与 neighborhood 两者与 price 的关系未知
heatmap(data=df, figsize=(6,5))

 

 9）方差分析

# 刚才的探索我们发现，style 与 neighborhood 的类别都是三类，
 ## 如果只是两类的话我们可以进行卡方检验，所以这里我们使用方差分析
    
## 利用回归模型中的方差分析
## 只有 statsmodels 有方差分析库
## 从线性回归结果中提取方差分析结果
import statsmodels.api as sm
from statsmodels.formula.api import ols # ols 为建立线性回归模型的统计学库
from statsmodels.stats.anova import anova_lm
# 数据集样本数量：6028，这里随机选择 600 条，如果希望分层抽样，可参考文章：
df = df.copy().sample(600)

# C 表示告诉 Python 这是分类变量，否则 Python 会当成连续变量使用
## 这里直接使用方差分析对所有分类变量进行检验
## 下面几行代码便是使用统计学库进行方差分析的标准姿势
lm = ols('price ~ C(neighborhood) + C(style)', data=df).fit()
anova_lm(lm)

# Residual 行表示模型不能解释的组内的，其他的是能解释的组间的
# df: 自由度（n-1）- 分类变量中的类别个数减1
# sum_sq: 总平方和（SSM），residual行的 sum_eq: SSE
# mean_sq: msm, residual行的 mean_sq: mse
# F：F 统计量，查看卡方分布表即可
# PR(>F): P 值

# 反复刷新几次，发现都很显著，所以这两个变量也挺值得放入模型中

 10）多元线性回归建模

from statsmodels.formula.api import ols

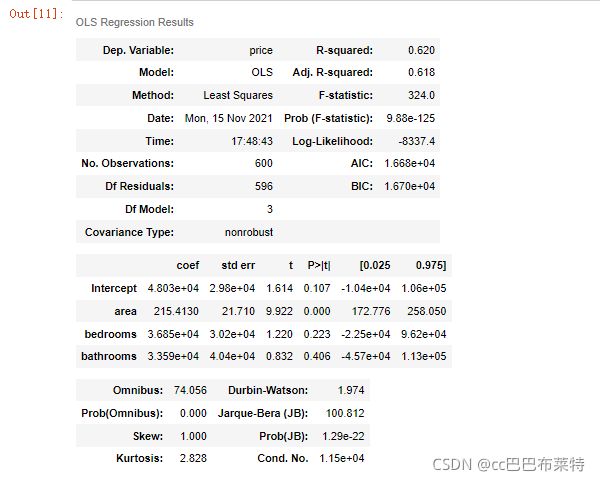
lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
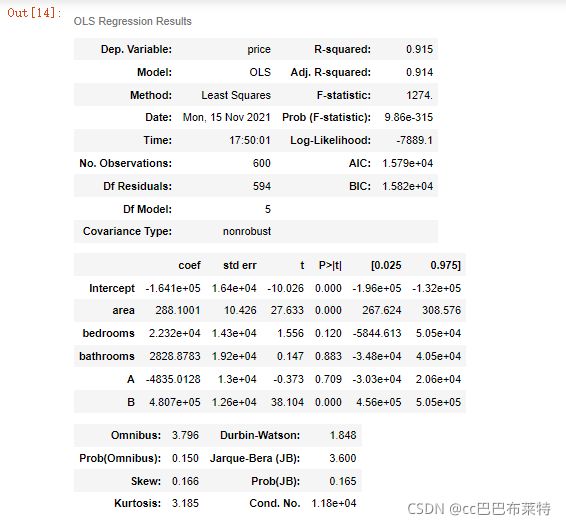
lm.summary()

OLS结果说明参考：用最小二乘法OLS做回归，并解读结果_Toby的博客-CSDN博客_ols回归结果解读 

 11）模型优化，通过添加虚拟变量与使用方差膨胀因子检测多元共线性的方式来提升模型精度

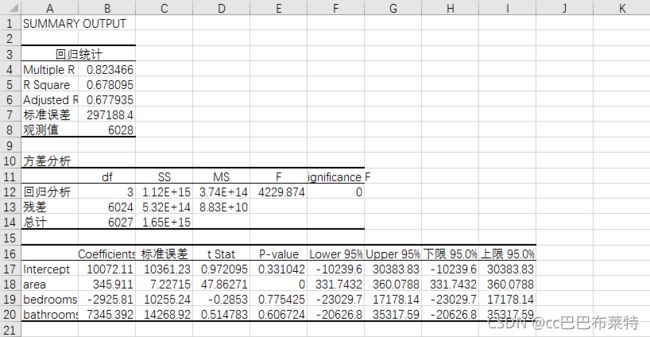
方差膨胀因子(Variance Inflation Factor，VIF)，是指解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比。VIF越大，显示共线性越严重。经验判断方法表明：当0

# 设置虚拟变量
# 以名义变量 neighborhood 街区为例
nominal_data = df['neighborhood']

# 设置虚拟变量
dummies = pd.get_dummies(nominal_data)
dummies.sample()  # pandas 会自动帮你命名

# 每个名义变量生成的虚拟变量中，需要各丢弃一个，这里以丢弃C为例
dummies.drop(columns=['C'], inplace=True)
dummies.sample()

# 将结果与原数据集拼接
results = pd.concat(objs=[df, dummies], axis='columns')  # 按照列来合并
results.sample(3)
# 对名义变量 style 的处理可自行尝试

 12）再次建模

lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()

结果输出：

13）自定义方差膨胀因子的检测公式

 def vif(df, col_i):
    """
    df: 整份数据
    col_i：被检测的列名
    """
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

14）调用方差膨胀因子的检测函数

test_data = results[['area', 'bedrooms', 'bathrooms', 'A', 'B']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))
# 发现 bedrooms 和 bathrooms 存在强相关性，可能这两个变量是解释同一个问题

        根据结果发现变量 bedrooms 和 bathrooms 的方差膨胀因子都超过了 10。其实方差因子通常成对出现，通常较大的两个方差膨胀因子表明这两个变量自身本来就具有高度相关性，即这两个变量一起才解释一种东西，可以考虑去除一个自己并不怎么感兴趣的变量即可，多重线性回归模型的主要假设之一是我们的预测变量彼此不相关，我们希望预测变量与反应变量相关，而不是彼此之间具有相关性。

15）去掉方差膨胀因子最大的变量 bedrooms，后再进行一次 ols 建模

lm = ols(formula='price ~ area + bathrooms + A + B', data=results).fit()
lm.summary()

16）再次进行多元共线性检测

test_data = df[['area', 'bathrooms']]
for i in test_data.columns:
    print(i, '\t', vif(df=test_data, col_i=i))

 

2、偏差数据

数据分析中的两种偏差：选择性偏差和幸存者偏差。

选择性偏差指的是在研究过程中因样本选择的非随机性而导致得到的结论存在偏差,是由于人为主观的选择而导致的数据偏差。

幸存者偏差指的是只能看到经过某种筛选而产生的结果，而没有意识到筛选的过程，因此忽略了被筛选掉的关键信息。

3、缺少数据的预处理（数据清洗）

缺少数据的预处理通常有三种处理方法：删除法、差补法和替换法。

删除法包括：1）删除观测样本；2）删除变量；3）使用完整原始数据进行分析；4）改变权重。

差补法包括：1）抽样填补；2）均值填补；3）回归模型；4）热平台差补；5）冷平台差补；6）拉格朗日插值法；7）随机森林插值。

替换法：缺失值所在变量为数值型：用该变量在其他所有对象的取值的均值/特定值来替换变量的缺失值；缺失值所在变量为非数值型：用该变量其他全部有效观测值的中位数或众数进行替换。

4、“特征共线性”的检测方法

多重共线性(Multicollinearity)是指线性回归模型中的自变量之间由于存在高难度相关关系而使模型的权重参数估计失真或难以估计准确的一种特性，多重是指一个自变量可能与多个其他自变量之间存在相关关系。检测方法常有经验式的诊断方法和统计检验方法。

三、用Excel重做上面的多元线性回归，求解回归方程

1）使用Excel打开house_prices.csv文件

 2）选择数据-->数据分析-->回归

 3）回归参数设置，选择area、bedrooms、bathrooms作为X，price作为Y求回归

4） 结果输出

        在上图中的回归统计子表中，字段Multiple R代表复相关系数R，也就是R^2的平方根，又称相关系数，用来衡量自变量x与y之间的相关程度的大小。本次数据集回归分析得到的R=0.823466，这表明x和y之间的关系为高度正相关。R Square是复测定数，也就是相关系数R的平方。Adjusted R Square是调整后的复测顶系数R^2，该值为0.677935，说明自变量能说明因变量y的67.79%，因变量y的32.21%要由其他因素来解释。标准误差是用来衡量拟合程度的大小，也用于计算与回归相关的其他统计量，此值越小，说明拟合程度越好。观察值是用于估计回归方程的数据的观察值个数。

        在上图中的第二张子表方差分析表，主要作用是通过F检验来判定回归模型的回归效果。Significance F为F检验显著性统计量，它的P值小于显著性水平0.05，故而能够确定该回归方程回归效果显著，且方程中至少有一个回归系数显著不为0。

        第三张子表，Coefficients为常数项和自变量的回归系数，根据上表可以估算得出回归方程为：y=345.911*area - 2925.81*bedrooms + 7345.392*bathrooms + 10072.11。但估算出的回归方程可能存在很大的误差，在第三张子表中更为重要的一列是P-value列，P-value为回归系数t统计量的P值。t值等于系数除以标准误，t值和p>|t|是一个意思，都是看回归结果是否显著，p>|t|越小越显著，对应的是10%、5%、1%水平显著。若是零，说明，在1%水平上都显著。由表中p-value的值可以发现，自变量area的P值远小于显著性水平0.05，因此area与price的相关性最强，bedrooms和bathrooms的P值大于显著性水平0.05，说明这两个自变量与y相关性比较弱。

5）截取部分price预测值

四、用机器学习库Sklearn库重做上面的多元线性回归

1）导入基础包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
import math
from sklearn import linear_model #线性模型

2）读取文件数据

#读取数据
data = pd.read_csv('D:\Downloads\house_prices.csv')
data.head()

 

3）去除掉house_id这一列元素

new_data=data.iloc[:,1:]#除掉Id这一行
new_data.head()

 

4）计算数值列的相关系数矩阵

new_data.corr()#相关系数矩阵，只统计数值列

 

5）根据上述结果可以发现area、bedrooms、bathroom和price的相关系数分别为0.823、0.743、0.735，取area、bedrooms、bathrooms作为X，price为Y求线性回归

x_data=new_data.iloc[:,1:4]#area、bedrooms、bathrooms对应列
y_data=new_data.iloc[:,-1]#price对应列
print(x_data,y_data,len(x_data))

 

6）应用模型计算回归方程

#应用模型
model = linear_model.LinearRegression() #最小二乘法线性回归
model.fit(x_data,y_data)#
print("回归系数：",model.coef_)
print("截距：",model.intercept_)
print("回归方程：price =",model.coef_[0],'*area +',model.coef_[1],'*bedrooms +',model.coef_[2],'*bathrooms + ',model.intercept_)

7）房价预测

linreg = linear_model.LinearRegression()
linreg.fit(x_data, y_data)
y_pred = linreg.predict(x_data)
print (y_pred)

五、三者的结果对比分析

        使用数学方法对影响变量的各种因素进行分析，可以快速确定自变量与因变量之间是否存在线性关系，能够帮助我们建立合适的数学模型。当不进行数据处理时，使用sklearn和excel进行数据分析的结果是一样的，但是进行了数据清理之后的基于统计分析库statsmodels进行数据分析得到的回归方程与前面两种相差较大，而进行多元共线性检测后，结果变得更合理了。

六、总结

        在做多元现行回归时，虽然自变量越多并不一定得到的结果就越准确，但多个自变量的最优组合共同来预测或估计因变量，比只用某些自变量进行预测或估计更有效，更符合实际。

参考文献：基于多元线性回归的房价预测_最烦起名字嗄的博客-CSDN博客_多元线性回归模型预测房价