python 逻辑回归，预测银行客户是否购买定期存款

问题：
逻辑回归其实是一个二分类问题，预测银行客户是否购买定期存款我们会提出以下一些问题：
(1)影响银行客户购买定期存款的因素有哪些
(2)对于类别变量我们应该怎样处理，
(3)我们应该怎样进行特征选择
(4)逻辑回归模型预测，以及最终的评估
另外还有很多需要注意的，比如数据处理，缺失值异常值的怎样处理，等等
下面开始一步步进行实现
首先导入在整个过程中需要用到的模块

import pandas as pd
import numpy as np
from sklearn import preprocessing
import matplotlib.pyplot as plt 
plt.rc("font", size=14)
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split #交叉验证时对数据集的切分
import seaborn as sns
sns.set(style="white")
sns.set(style="whitegrid", color_codes=True)

数据集的导入（数据集的地址https://raw.githubusercontent.com/madmashup/targeted-marketing-predictive-engine/master/banking.csv）

#数据进行相应的处理
data=pd.read_csv(r'C:\Users\ASUS PC\Desktop\lr_data.csv',delimiter=',')
data=data.dropna()
print(data.shape)
print(list(data.columns))
data.head()

部分特征解释
‘age’：年龄
‘job’,：工作
‘marital’：婚姻状态
‘education’：教育
‘default’：默认：有信用违约？（：“绝对没有”、“是”、“unknown”）
‘housing’：住房贷款有吗？（：“绝对没有”、“是”、“unknown”）
‘loan’：贷款有吗？
‘contact’,通信型（绝对接触：接触：“泡沫塑料”，“电话”）
‘month’：年月（绝对：“1”、“2”、“3”，…，“11”、“12”）
‘day_of_week’, 周（Day of the contact绝对：“我”、“你”、“wed”、“Thu”、“星期五”）
‘duration’：接触时间：last duration，seconds（0.54）。
‘campaign’,
‘pdays’,
‘previous’,
‘poutcome’
‘emp_var_rate’：就业变化率
‘cons_price_idx’,消费者价格
‘cons_conf_idx’：消费者信息
‘euribor3m’
‘nr_employed’
‘y’
拿到数据就先看看数据都有哪些特征，然后处理一些异常值缺失值等。
为了更好的的建立模型，可以将一部分的数据进行处理，比如可以把教育这一特征进行适当的处理，可以把basic.4y， ‘basic.9y’,‘basic.6y’,合并在一起，生成新的basic

data['education'].unique()

array(['basic.4y', 'unknown', 'university.degree', 'high.school',
       'basic.9y', 'professional.course', 'basic.6y', 'illiterate'], dtype=object)

将三个 basic的教育类型用basic代替

data['education']=np.where(data['education']=='basic.4y','basic',data['education'])
data['education']=np.where(data['education']=='basic.6y','basic',data['education'])
data['education']=np.where(data['education']=='basic.9y','basic',data['education'])
data['education'].unique()

结果

array(['basic', 'unknown', 'university.degree', 'high.school',
       'professional.course', 'illiterate'], dtype=object)

这样就减少了教育的类别，这样有助于模型的建立。
可以用以下代码将原数据的特征的部分信息进行展示

data.info()

结果：

age               41188 non-null int64
job               41188 non-null object
marital           41188 non-null object
education         41188 non-null object
default           41188 non-null object
housing           41188 non-null object
loan              41188 non-null object
contact           41188 non-null object
month             41188 non-null object
day_of_week       41188 non-null object
duration          41188 non-null int64
campaign          41188 non-null int64
pdays             41188 non-null int64
previous          41188 non-null int64
poutcome          41188 non-null object
emp_var_rate      41188 non-null float64
cons_price_idx    41188 non-null float64
cons_conf_idx     41188 non-null float64
euribor3m         41188 non-null float64
nr_employed       41188 non-null float64
y                 41188 non-null int64
dtypes: float64(5), int64(6), object(10)
memory usage: 6.9+ MB

从以上结果显示，各个特征都不存在缺失值了，另外还可以看见各个特征的数据类型。 (注意有些时候还需要对数据进行归一化处理，这里先不进行归一化处理，看看结果，等会再给归一化后的结果)，下面展示一下不同类别（y,取0，1）的数据。并进行可视化展示

data['y'].value_counts()
sns.countplot(x='y',data=data,palette='hls')
plt.show()

结果：

从以上结果显示，0，1两类的数据量。
可以根据分组的比较各个指标与y分类的关系

data.groupby('y').mean()

结果为：

	age	duration	campaign	pdays	previous	emp_var_rate	cons_price_idx	cons_conf_idx	euribor3m	nr_employed
y										
0	39.911185	220.844807	2.633085	984.113878	0.132374	0.248875	93.603757	-40.593097	3.811491	5176.166600
1	40.913147	553.191164	2.051724	792.035560	0.492672	-1.233448	93.354386	-39.789784	2.123135	5095.115991

可以看出：
duration，pdays，emp_var_rate这三个特征在0,1分类中存在比较大的差异，另外还可以从结果显示，购买定期存款的平均年龄要高于不购买的。为了查看其他的特征对是否购买的影响，可以进行分组查看。

data.groupby('education').mean()

结果显示居然是文盲购买顶起存款最多。

#工作和y的关系
pd.crosstab(data.job,data.y).plot(kind='bar')
plt.title('Purchase Frequency for Job Title')
plt.xlabel('Job')
plt.ylabel('Frequency of Purchase')
#plt.savefig('purchase_fre_job')
plt.show()

结果：

从图中结果显示，购买定期存款与工作有比较大的关系，可以认为因此，职称可以是结果变量的良好预测因子。

table=pd.crosstab(data.marital,data.y)
table.div(table.sum(axis=1).astype(float), axis=0).plot(kind='bar', stacked=True)
plt.title('Stacked Bar Chart of Marital Status vs Purchase')
plt.xlabel('Marital Status')
plt.ylabel('Proportion of Customers')
plt.show()

从图中显示婚姻状况似乎不是结果变量的强预测因子。

教育情况与y的关系
table=pd.crosstab(data.education,data.y)
table.div(table.sum(axis=1).astype(float),axis=0).plot(kind='bar')
plt.title('Stacked Bar Chart of Education Status vs Purchase')
plt.xlabel('Education Status')
plt.ylabel('Proportion of Customers')
plt.show()

虽然哦那个以上图中显示差别不是特别的大，但是还是存在有几个变量间的差距有点大，似乎可以把该变量作为预测因子。

#day_of_week与y的关系：
pd.crosstab(data.day_of_week,data.y).plot(kind='bar')
plt.title('Purchase Frequency for Day of Week')
plt.xlabel('Day of Week')
plt.ylabel('Frequency of Purchase')
plt.savefig('pur_dayofweek_bar')
plt.show()

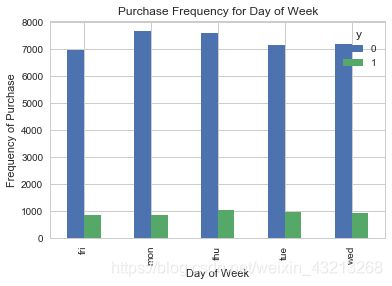
该特征对于结果好像不是特别的明显，可以认为该特征对结果影响不大，似乎不是结果的良好预测因子。

 　#　month与y的关系
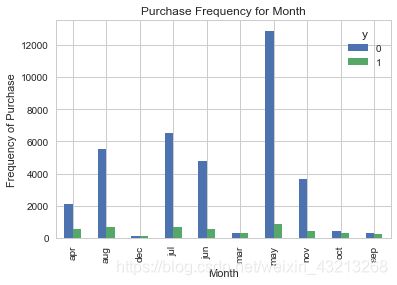
pd.crosstab(data.month,data.y).plot(kind='bar')
plt.title('Purchase Frequency for Month')
plt.xlabel('Month')
plt.ylabel('Frequency of Purchase')
plt.savefig('pur_fre_month_bar')
plt.show()

似乎可以认为month是一个良好的预测因子。

#poutcome与y的关系：
pd.crosstab(data.poutcome,data.y).plot(kind='bar')
plt.title('Purchase Frequency for Poutcome')
plt.xlabel('Poutcome')
plt.ylabel('Frequency of Purchase')
plt.show()

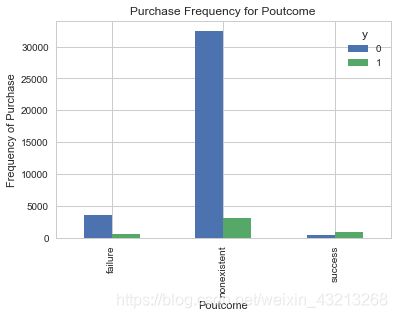
认为 poutcome是一个良好的预测指标。
根据数据中的显示有10个object变量，需要对类别变量进行转化，
对于类别变量的转换，可以参考

cat_vars=['job','marital','education','default','housing','loan','contact','month','day_of_week','poutcome']
for var in cat_vars:
    cat_list='var'+'_'+var
    cat_list = pd.get_dummies(data[var], prefix=var)#prefix表示增加前缀
    data1=data.join(cat_list)
    data=data1
data_vars=data.columns.values.tolist()
to_keep=[i for i in data_vars if i not in cat_vars]
data_final=data[to_keep]
data_final.columns.values

注意查看哑变量原理

# 分离特征与目标变量
data_final_vars=data_final.columns.values.tolist()
y=['y']
X=[i for i in data_final_vars if i not in y]

  特征选择　
　递归特征消除（Recursive Feature Elimination，RFE）基于以下思想：
首先，在初始特征集上训练估计器，并且通过coef_属性或通feature_importances_属性获得每个特征的重要性。 然后，从当前的一组特征中删除最不重要的特征。
 在修剪的集合上递归地重复该过程，直到最终到达所需数量的要选择的特征。

代码实现

from sklearn import datasets
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
rfe = RFE(logreg, 18)
rfe = rfe.fit(data_final[X], data_final[y] )
print(rfe.support_)
print(rfe.ranking_)#当结果是1表示该特征比较重要，被选出来

# 根据布尔值筛选我们想要的特征(参考）：
from itertools import compress

cols=list(compress(X,rfe.support_))
cols

执行模型：

import statsmodels.api as sm
X=data_final[cols]
y=data_final['y']
logit_model=sm.Logit(y,X)
logit_model.raise_on_perfect_prediction = False
result=logit_model.fit()
print(result.summary().as_text)

大多数变量的p值小于0.05，因此，大多数变量对模型都很重要。

逻辑回归模型的拟合
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
y_pred = logreg.predict(X_test)
print('Accuracy of logistic regression classifier on test set: {:.2f}'.format(logreg.score(X_test, y_test))) 

交叉验证
from sklearn import model_selection
from sklearn.model_selection import cross_val_score

kfold = model_selection.KFold(n_splits=10, random_state=7)
modelCV = LogisticRegression()
scoring = 'accuracy'
results = model_selection.cross_val_score(modelCV, X_train, y_train, cv=kfold, scoring=scoring)
print("10-fold cross validation average accuracy: %.3f" % (results.mean()))

交叉验证尝试避免过度拟合，同时仍然为每个观察数据集生成预测。
我们使用10折交叉验证来训练我们的Logistic回归模型。平均精度仍然非常接近Logistic回归模型的准确度; 因此，我们可以得出结论，我们的模型很好拟合了数据。

混淆矩阵：
Confusion Matrix
from sklearn.metrics import confusion_matrix
confusion_matrix = confusion_matrix(y_test, y_pred)
print(confusion_matrix)

计算精度（precision）召回(recall)F测量(F-measure)和支持(support) 精度是比率tp /（tp + fp），其中tp是真阳性的数量，fp是假阳性的数量。 精确度直观地是分类器如果是负的则不将样品标记为阳性的能力。

召回是比率tp /（tp + fn）其中tp是真阳性的数量，fn是假阴性的数量。 召回直观地是分类器找到所有阳性样本的能力。

F-beta分数可以解释为精确度和召回率的加权调和平均值，其中F-β分数在1处达到其最佳值，在0处达到最差分数。

F-beta评分对召回的重量超过精确度β因子。 beta = 1.0意味着召回和精确度同样重要。

支持是y_test中每个类的出现次数。

from sklearn.metrics import classification_report

print(classification_report(y_test, y_pred))

可以看出：在整个测试集中，88％的促销定期存款是客户喜欢的定期存款。 在整个测试集中，90％的客户首选定期存款。

from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred, average = 'macro'))

#ROC曲线
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve

logit_roc_auc = roc_auc_score(y_test, logreg.predict(X_test))
fpr, tpr, thresholds = roc_curve(y_test, logreg.predict_proba(X_test)[:,1])
plt.figure()
plt.plot(fpr, tpr, label='Logistic Regression (area = %0.2f)' % logit_roc_auc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right")
#plt.savefig('Log_ROC')
plt.show()

ROC曲线是与二元分类器一起使用的另一种常用工具。 虚线表示纯随机分类器的ROC曲线; 一个好的分类器尽可能远离该线（朝左上角）