【Paper Reading FedBCD: A Communication-Efficient Collaborative Learning Framework for DF

FedBCD: A Communication-Efficient Collaborative Learning Framework for Distributed Features

原文来源：[TSP2022] FedBCD: A Communication-Efficient Collaborative Learning Framework for Distributed Features

欢迎大家访问我的GitHub博客

https://lunan0320.cn

FedBCD：一种面向分布式特征的高效率通信协作学习框架

1. Abstract

纵向联邦学习：多主体multi-parties、分布式特征下的协作学习 ，适用于用户重叠多、特征互补（样本相同、特征不同）的场景

多主体在每次迭代时需要实时交换梯度更新信息来进行联合计算和训练，通信效率是主要瓶颈。

对比：基于样本分割的横向联邦学习，使用较多的是FedAvg，运行SGD并进行多次本地局部更新，实现了更好的通信效率。（联邦平均）

但是，基于特征分割的纵向联邦学习中，每次迭代的梯度计算需要各参与方共同协作而非简单加权平均。

（在保证理论收敛率的情况下，在每次通信前进行足够数量的局部更新，来解决昂贵的通信开销问题）

2. Introduction

2.1 Background

大多数联邦学习框架，数据是按照样本分布的，共享相同集合的属性。

但是，另一个场景是 parties 共享相同用户的不同特征

在sample-partitioned FL中，FedAvg可以有效减少通信的次数

但是对于feature-partitioned FL，有两个问题：

1. multiple local update不清楚是否起作用

2. attacks： share gradietns时候会泄露原始数据

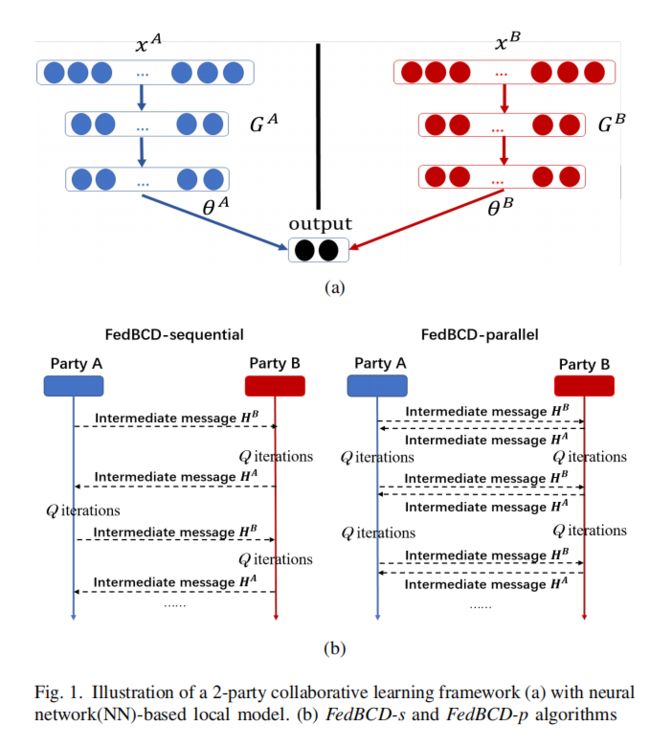
2.2 FedBCD

Federated stochastic block coordinate descent (FedBCD)

• FedAvg：适用于sample-partitioned场景，global model的参数是在多个局部更新后被平均

• FedBCD: 适用于feature-partitioned场景，模型参数和特征的子集可以独立执行多次局部更新

文章证明了：

1. 适当选择 local updates的数量，mini-batch的大小，以及learning rates可以使得收敛到O(1*/* √ T) accuracy with O( √ T) rounds
2. 提供安全性证明。在训练过程中，不管进行多少次迭代、通信多少信息都不会泄露原始数据

3. Related Work

3.1 Sample-partitioned

传统分布式学习采用PS架构来聚合本地的updates

分析：

1、 安全性

2、 收敛性

3.2 Feature-partitioned

模型：树形、线性、逻辑回归、神经网络

Distributed Coordinate Descent: 平衡划分banlanced partitions、解耦计算decoupled computation

Distributed Block Coordinate Descent：执行同步的block updates

Our approach： 强调通信开销是主导，进行足够数量的local updates。假设只有一方有labels，其他方只有与他通信来减小信息交换。

3.2 Privacy Preserving

HE、MPC但是会带来昂贵的数据通信和计算量。

DP是会导致模型精度缺失

或者是混合的方法，但是这也就是一个trade-off，在模型准确性和安全性之间权衡

4. Problem Definition

K个parties，N个samples，d_k是第k个party的特征维度

假设第K个party持有所有数据的 labels，前K-1个parties只有特征向量x

训练问题可以归纳为：

f (·) 是loss function，y (·) 是regularizer正则项

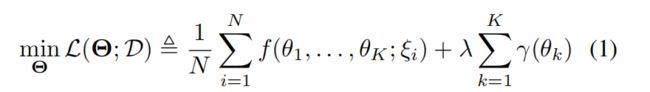
损失函数Loss Function形式如下：

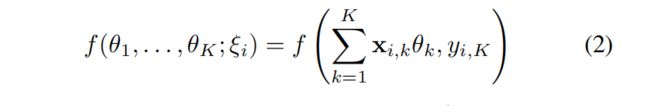
目的是：对于每个参与party k ，在不对外共享它的数据和参数的情况下，找到θ_k

5. The Proposed FedBCD Algorithms

5.1 Prior Definition

对于一个mini-batch S，第k个party的随机部分梯度如下：

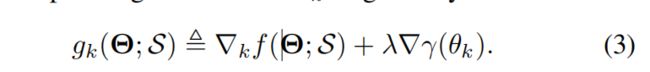
之后，定义变量H如下（类似wx+b）

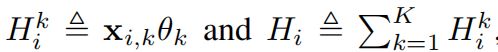
重新得到 Loss Function:

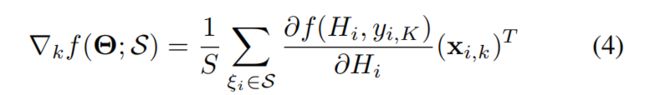
为了在本地计算 f(·)， 每个party k 会发送

给第K个party，然后party K就计算出梯度值：
$$I_S^{K,q}=\frac{\partial f(H_i,y_{i,K})}{\partial H_i}i\in S$$
然后第K个party把这个
$$I^{K,q}$$

发送给其他的parties，最终all parties都可以计算梯度updates

定义变量 I 是计算所需要的信息:

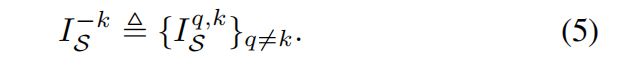
得到随机梯度下降的公式：

总的随机梯度下降如下：

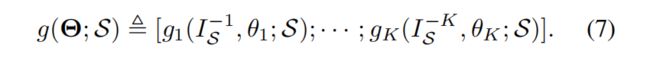
5.2 最直接的方法：FedSGD

缺点：每轮都需要计算中间结果，开销大，通信负担重。（每次迭代都需要一次通信）

5.3 改进的方法：FedBCD

在并行通信（FedBCD-p）或者顺序通信 (FedBCD-s) 之前，每个party都要执行Q 次连续的本地梯度更新

Q = 1 时候，退化为FedAvg

5.4 算法细节

缺点：I_{s} ^{-k} 是从最近同步的通信中得到的中间结果，因此在本地重复计算g_k时候就可能不是真实梯度的无偏估计

在本地进行的Q次updates中，是没有party之间的通信的

因此，这里也有一个trade-off 在通信效率和计算效率之间。

6. Convergence Analysis

关注并行和串行两个version

Assumption：

1. Uniform Sampling

​ S是从D中均匀取样得到的，符合IID

2. Bounded Variance

方差有界（梯度估计值和真实值之间的差距是在一定范围内）

3. Lipschitz Gradient

   

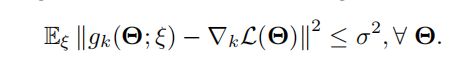
Remark1：对于 local 随机梯度下降很难找到一个关于梯度的无偏估计，因为是使用了之前最新同步的数据做了Q次连续的本地迭代

Remark2：分析了选择 T、learning rate 和Q来实现较高准确率的关系

Remark3: 分析了学习率和Q是第一个对于基于特征的联邦学习实现的高准确率的model

Remark4：分析了通信轮数大大减少，通过 multiple local updates节省了通信

Remark5: 分析了节点数K和batch size S的影响

7. Security Analysis

是否一方可以在训练过程中从交换的信息中得到其他方的数据向量？

• 之前的研究是表明数据的泄露是从模型参数和梯度中透露出去的，但是FedBCD中参数是保密的，只有中间结果传输（模型参数和特征的内积）

• 传输梯度也是降维维数的梯度，而不是梯度本身，因此可以抵抗传统的攻击，可以在很多轮数的迭代通信之后仍然不泄露信息

8. Experiments

8.1 Dataset and Models

MIMIC-III

31 million clinical events，对应17个变量，在给定7个时间序列上计算6个不同的样本特征，得到17*7*6=714个特征，直接按照特征划分（实际情况需要结合不同的医院或者同一医院的不同部门）

NUS-WIDE

包括634 个 low-level 的图像

将图像特征分配给一个party，文本特征分配给另一个party

MNIST

直接将MNIST图像垂直分为两个parties

28*28*1的图像划分为两个28*14*1的图像

通过卷积，再全连接层，再logistic regression

Default-Credit

划分为15个人口统计学特征和18个支付特征(通常发生在银行风险预测上)

基于同态加密完成一个联邦迁移学习FTL

对于实验部分，都采用的是decay learning rate
$${\eta }^r=\frac{{\eta }^0}{\sqrt{r+1}}$$

8.2 Evaluation Metric

考虑两方面：

1. Training Loss

​ 在训练集中被评估

2. Area Under Curve（AUC）

​ under the receiver operating characteristics (ROC)

​ 表示的是预测的准确性？（界于0-1，0表示对每个sample都预测错误）

目标：最小化Training loss，最大化AUC

8.3 Results and Discussion

8.3.1 FedBCD-p vs FedBCD-s

在MIMIC-LR andMNIST-CNN 上变化本地迭代的轮数 Q

运行相同的轮数，FedBCD-s所需时间是FedBCD-p的两倍。

随着局部迭代数量的增大，所需要的通信次数显著减少。

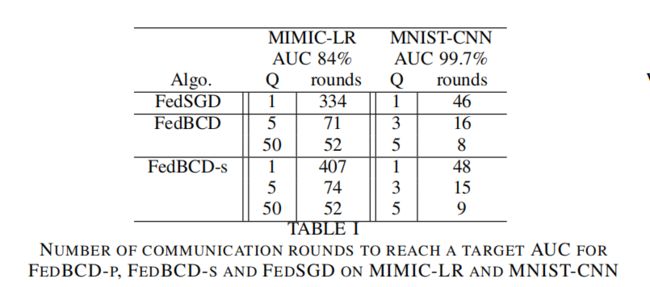
因此，可以合理的增加本地迭代的次数，来利用并行的优势，这样通过减少通信次数来可以节省通信开销

8.3.2 Impact of Q

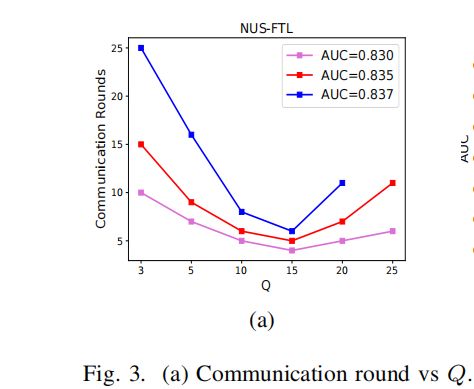
探究了收敛率与本地迭代次数Q的关系

在NUS-FTL上用大范围的Q来评估FedBCD-p

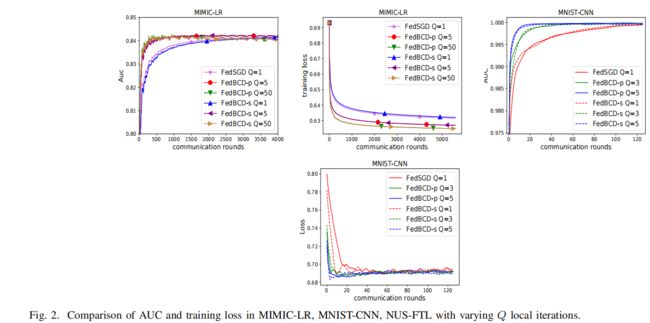
Q = 15时候，FedBCD-p能够在最短的通信轮数下达到最好的AUC

对于每个AUC，都存在一个最优的Q。因此，要找到一个最合适的Q来实现最好的通信效率

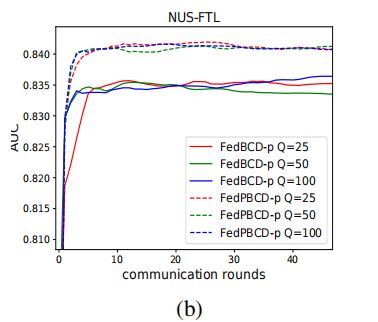
下图展示了对于很大的Q，比如25，50，100，此时FedBCD-p不能收敛到AUC的83.7%

8.3.3 Proximal Gradient Descent

在本地目标函数上加一个proximal term，来缓解当本地迭代次数较多情况下的分歧

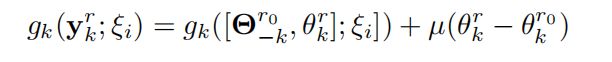
加上的这一项其实就是

的梯度。使用初始的参数来限制本地更新。这也叫FedPBCD-p

下图证明了在Q比较大的时候，FedBCD-p收敛效果较差，但是FedPBCD-p收敛效果较好

8.3.4 Increasing number of Parties

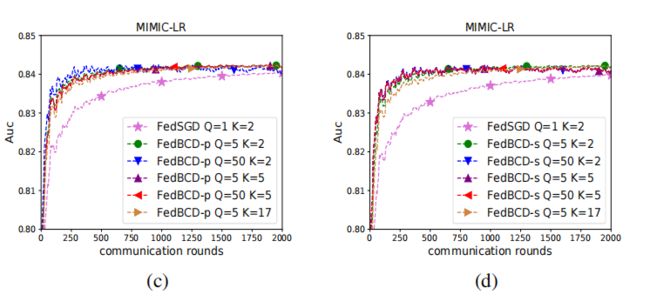
在MIMIC-LR数据集下增加了parties的数量K到5或者17

根据clinical variables划分，每个party有相同变量的所有特征

采用了 decay learning rate
$$\frac{{\eta }^0}{\sqrt{(r+1)\times K}}$$

如下图所示，K的变化影响是非常微弱的

8.3.5 Implementation with HE

分析使用HE后，对于FedBCD-p效率的影响

使用HE极大程度上提高了安全性，但是对于加密后的数据进行运算是计算量较大的

增大本地迭代轮数Q的同时可以减少通信轮数，但是并不意味着会减小计算开销，因为这与总的轮数有关，而总的轮数是可能变多的

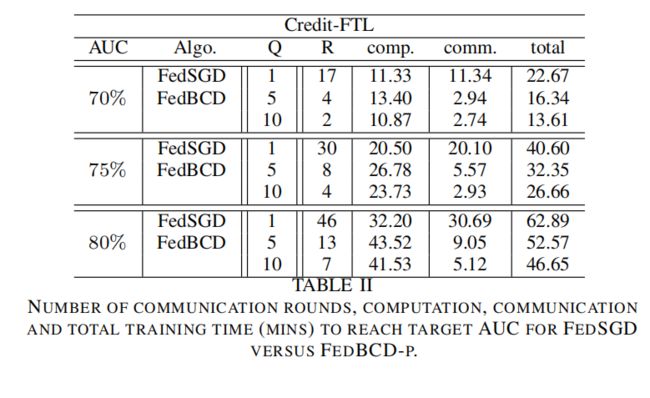
Q越大，通信轮数越少，总的训练时间也会变少，计算时间也是略有增加，当Q = 10时候，通信轮数减少了70%

9. Conclusions and Future Work

• 本文提出了一个联邦学习框架，各个参与方在通信之前需要在本地迭代多次

• 证明了原始数据不会泄露

• FedBCD显著的减少了通信的轮数以及总的通信开销。

• 使用decay learning rate以及恰当的选择本地迭代次数Q可以很好的达到全局的收敛

• 继续探究更复杂的以及异步协同的系统