机器学习之聚类学习笔记-利用python的sklearn实现
学习来源
sklearn中文文档

聚类算法练习
python代码实现K-means算法
Python数模笔记-Sklearn(2)聚类分析
均值偏移聚类
K-means聚类算法
该算法可分为三个步骤。第一步是选择初始质心,最基本的方法是从 X 数据集中选择 k 个样本。初始化完成后,K-means 由接下来两个步骤之间的循环组成。 第一步将每个样本分配到其最近的质心。第二步通过取分配给每个先前质心的所有样本的平均值来创建新的质心。计算旧的和新的质心之间的差异,并且算法重复这些最后的两个步骤,直到该值小于阈值。换句话说,算法重复这个步骤,直到质心不再显著移动。
from sklearn.cluster import KMeans # 导入 sklearn.cluster.KMeans 类
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
kmCluster = KMeans(n_clusters=2).fit(X) # 建立模型并进行聚类,设定 K=2
print(kmCluster.cluster_centers_) # 返回每个聚类中心的坐标
# [[10., 2.], [ 1., 2.]] # print 显示聚类中心坐标
print(kmCluster.labels_) # 返回样本集的分类结果
# [1, 1, 1, 0, 0, 0] # print 显示分类结果
print(kmCluster.predict([[0, 0], [12, 3]])) # 根据模型聚类结果进行预测判断
# [1, 0] # print显示判断结果:样本属于哪个类别
[[10. 2.]
[ 1. 2.]]
[1 1 1 0 0 0]
[1 0]
改进
from sklearn.cluster import MiniBatchKMeans # 导入 MiniBatchKMeans 类
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 0], [4, 4],
[4, 5], [0, 1], [2, 2], [3, 2], [5, 5], [1, -1]])
# fit on the whole data
mbkmCluster = MiniBatchKMeans(n_clusters=2, batch_size=6, max_iter=10).fit(X)
print(mbkmCluster.cluster_centers_) # 返回每个聚类中心的坐标
# [[3.96,2.41], [1.12,1.39]] # print 显示内容
print(mbkmCluster.labels_) # 返回样本集的分类结果
# [1 1 1 0 0 0 0 1 1 0 0 1] # print 显示内容
print(mbkmCluster.predict([[0, 0], [4, 5]])) # 根据模型聚类结果进行预测判断
# [1, 0] # 显示判断结果:样本属于哪个类别
[[1.8115942 0.84057971]
[3.47058824 3.88235294]]
[0 1 0 1 0 1 1 0 0 0 1 0]
[0 1]
示例1
import sys
sys.path.append('/home/aistudio/external-libraries')
from numpy import *
def loadDataSet(fileName): # general function to parse tab -delimited floats
dataMat = [] # assume last column is target value
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float, curLine)) # map all elements to float()
dataMat.append(fltLine)
return dataMat
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # la.norm(vecA-vecB)
def randCent(dataSet, k):
n = shape(dataSet)[1]
centroids = mat(zeros((k, n))) # create centroid mat
for j in range(n): # create random cluster centers, within bounds of each dimension
minJ = min(dataSet[:, j])
rangeJ = float(max(dataSet[:, j]) - minJ)
centroids[:, j] = mat(minJ + rangeJ * random.rand(k, 1))
return centroids
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m, 2))) # create mat to assign data points
# to a centroid, also holds SE of each point
centroids = createCent(dataSet, k)
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m): # for each data point assign it to the closest centroid
minDist = inf;
minIndex = -1
for j in range(k):
distJI = distMeas(centroids[j, :], dataSet[i, :])
if distJI < minDist:
minDist = distJI;
minIndex = j
if clusterAssment[i, 0] != minIndex: clusterChanged = True
clusterAssment[i, :] = minIndex, minDist ** 2
print(centroids)
for cent in range(k): # recalculate centroids
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]] # get all the point in this cluster
centroids[cent, :] = mean(ptsInClust, axis=0) # assign centroid to mean
return centroids, clusterAssment
# --------------------测试----------------------------------------------------
# 用测试数据及测试kmeans算法
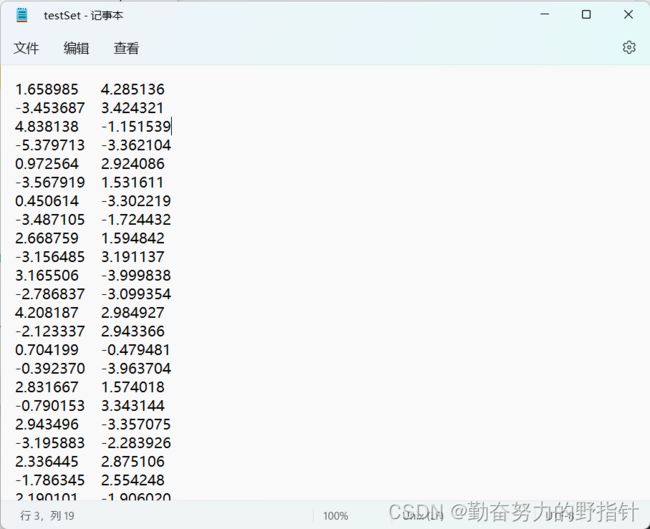
datMat = mat(loadDataSet('testSet.txt'))
myCentroids, clustAssing = kMeans(datMat, 4)
print(myCentroids)
print(clustAssing)
[[-2.69448004 -1.33016593]
[ 3.43028199 4.22204968]
[-1.11578762 -3.34756855]
[ 2.60732811 4.69286465]]
[[-3.19458313 0.22942845]
[ 3.193015 2.29036194]
[ 1.38105908 -3.08855729]
[ 0.72326244 3.856822 ]]
[[-3.30007281 -0.44935216]
[ 3.13799847 2.35490324]
[ 2.2166992 -3.04263975]
[-0.033335 3.59480045]]
[[-3.54251791 -2.066412 ]
[ 2.88949319 2.86832181]
[ 2.65077367 -2.79019029]
[-1.43546415 3.22862095]]
[[-3.53973889 -2.89384326]
[ 2.6265299 3.10868015]
[ 2.65077367 -2.79019029]
[-2.46154315 2.78737555]]
[[-3.53973889 -2.89384326]
[ 2.6265299 3.10868015]
[ 2.65077367 -2.79019029]
[-2.46154315 2.78737555]]
[[ 1. 2.3201915 ]
[ 3. 1.39004893]
[ 2. 7.46974076]
[ 0. 3.60477283]
[ 1. 2.7696782 ]
[ 3. 2.80101213]
[ 2. 5.10287596]
[ 0. 1.37029303]
[ 1. 2.29348924]
[ 3. 0.64596748]
[ 2. 1.72819697]
[ 0. 0.60909593]
[ 1. 2.51695402]
[ 3. 0.13871642]
[ 2. 9.12853034]
[ 2. 10.63785781]
[ 1. 2.39726914]
[ 3. 3.1024236 ]
[ 2. 0.40704464]
[ 0. 0.49023594]
[ 1. 0.13870613]
[ 3. 0.510241 ]
[ 2. 0.9939764 ]
[ 0. 0.03195031]
[ 1. 1.31601105]
[ 3. 0.90820377]
[ 2. 0.54477501]
[ 0. 0.31668166]
[ 1. 0.21378662]
[ 3. 4.05632356]
[ 2. 4.44962474]
[ 0. 0.41852436]
[ 1. 0.47614274]
[ 3. 1.5441411 ]
[ 2. 6.83764117]
[ 0. 1.28690535]
[ 1. 4.87745774]
[ 3. 3.12703929]
[ 2. 0.05182929]
[ 0. 0.21846598]
[ 1. 0.8849557 ]
[ 3. 0.0798871 ]
[ 2. 0.66874131]
[ 0. 3.80369324]
[ 1. 0.09325235]
[ 3. 0.91370546]
[ 2. 1.24487442]
[ 0. 0.26256416]
[ 1. 0.94698784]
[ 3. 2.63836399]
[ 2. 0.31170066]
[ 0. 1.70528559]
[ 1. 5.46768776]
[ 3. 5.73153563]
[ 2. 0.22210601]
[ 0. 0.22758842]
[ 1. 1.32864695]
[ 3. 0.02380325]
[ 2. 0.76751052]
[ 0. 0.59634253]
[ 1. 0.45550286]
[ 3. 0.01962128]
[ 2. 2.04544706]
[ 0. 1.72614177]
[ 1. 1.2636401 ]
[ 3. 1.33108375]
[ 2. 0.19026129]
[ 0. 0.83327924]
[ 1. 0.09525163]
[ 3. 0.62512976]
[ 2. 0.83358364]
[ 0. 1.62463639]
[ 1. 6.39227291]
[ 3. 0.20120037]
[ 2. 4.12455116]
[ 0. 1.11099937]
[ 1. 0.07060147]
[ 3. 0.2599013 ]
[ 2. 4.39510824]
[ 0. 1.86578044]]
示例2
from numpy import *
from matplotlib import pyplot as plt
def load_data_set(testSet):
"""加载数据集"""
dataSet = [] # 初始化一个空列表
fr = open(testSet)
for line in fr.readlines():
# 按tab分割字段,将每行元素分割为list的元素
curLine = line.strip().split('\t')
# 用list函数把map函数返回的迭代器遍历展开成一个列表
# 其中map(float, curLine)表示把列表的每个值用float函数转成float型,并返回迭代器
fltLine = list(map(float, curLine))
dataSet.append(fltLine)
return dataSet
def distance_euclidean(vector1, vector2):
"""计算欧氏距离"""
return sqrt(sum(power(vector1 - vector2, 2))) # 返回两个向量的距离
def rand_center(dataSet, k):
"""构建一个包含K个随机质心的集合"""
n = shape(dataSet)[1] # 获取样本特征值
# 初始化质心,创建(k,n)个以0填充的矩阵
centroids = mat(zeros((k, n))) # 每个质心有n个坐标值,总共要k个质心
# 遍历特征值
for j in range(n):
# 计算每一列的最小值
minJ = min(dataSet[:, j])
# 计算每一列的范围值
rangeJ = float(max(dataSet[:, j]) - minJ)
# 计算每一列的质心,并将其赋给centroids
centroids[:, j] = minJ + rangeJ * random.rand(k, 1)
return centroids # 返回质心
def k_means(dataSet, k, distMeas=distance_euclidean, creatCent=rand_center):
"""K-means聚类算法"""
m = shape(dataSet)[0] # 行数
# 建立簇分配结果矩阵,第一列存放该数据所属中心点,第二列是该数据到中心点的距离
clusterAssment = mat(zeros((m, 2)))
centroids = creatCent(dataSet, k) # 质心,即聚类点
# 用来判定聚类是否收敛
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m): # 把每一个数据划分到离他最近的中心点
minDist = inf # 无穷大
minIndex = -1 # 初始化
for j in range(k):
# 计算各点与新的聚类中心的距离
distJI = distMeas(centroids[j, :], dataSet[i, :])
if distJI < minDist:
# 如果第i个数据点到第j中心点更近,则将i归属为j
minDist = distJI
minIndex = j
# 如果分配发生变化,则需要继续迭代
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
# 并将第i个数据点的分配情况存入字典
clusterAssment[i, :] = minIndex, minDist ** 2
print(centroids)
for cent in range(k): # 重新计算中心点
# 去第一列等于cent的所有列
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]]
# 算出这些数据的中心点
centroids[cent, :] = mean(ptsInClust, axis=0)
return centroids, clusterAssment
datMat = mat(load_data_set('testSet.txt'))
myCentroids, clusterAssing = k_means(datMat, 4)
print(myCentroids)
print(clusterAssing)
datMat = mat(load_data_set('testSet.txt'))
myCentroids, clusterAssing = k_means(datMat, 4)
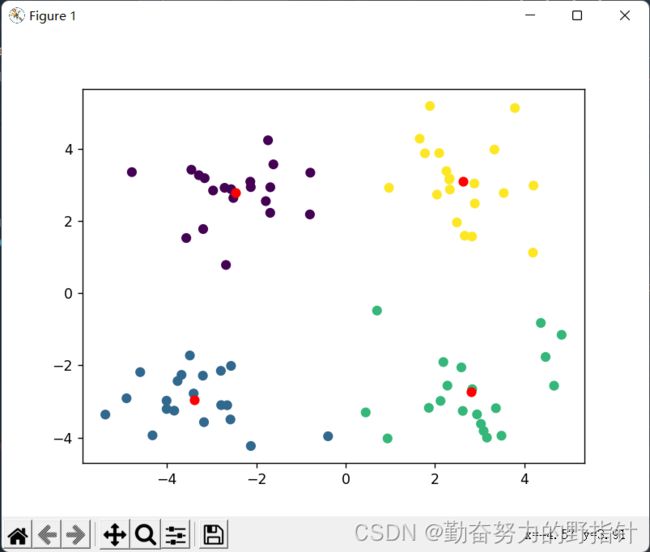
plt.scatter(array(datMat)[:, 0], array(datMat)[:, 1], c=array(clusterAssing)[:, 0].T)
plt.scatter(myCentroids[:, 0].tolist(), myCentroids[:, 1].tolist(), c="r")
plt.show()
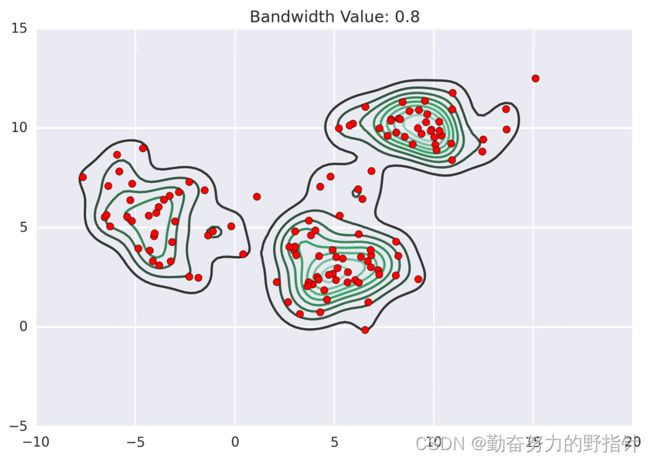
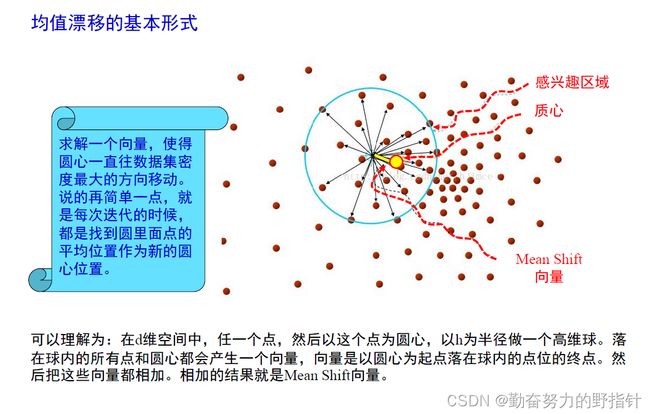
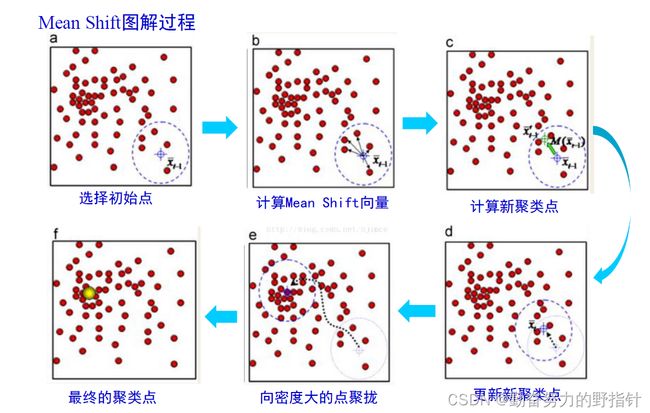
均值漂移聚类算法
均值漂移聚类是基于滑动窗口的算法,来找到数据点的密集区域。这是一个基于质心的算法,通过将中心点的候选点更新为滑动窗口内点的均值来完成,来定位每个组/类的中心点。然后对这些候选窗口进行相似窗口进行去除,最终形成中心点集及相应的分组。
- 确定滑动窗口半径r,以随机选取的中心点C半径为r的圆形滑动窗口开始滑动。均值漂移类似一种爬山算法,在每一次迭代中向密度更高的区域移动,直到收敛。
- 每一次滑动到新的区域,计算滑动窗口内的均值来作为中心点,滑动窗口内的点的数量为窗口内的密度。在每一次移动中,窗口会想密度更高的区域移动。
- 移动窗口,计算窗口内的中心点以及窗口内的密度,知道没有方向在窗口内可以容纳更多的点,即一直移动到圆内密度不再增加为止。
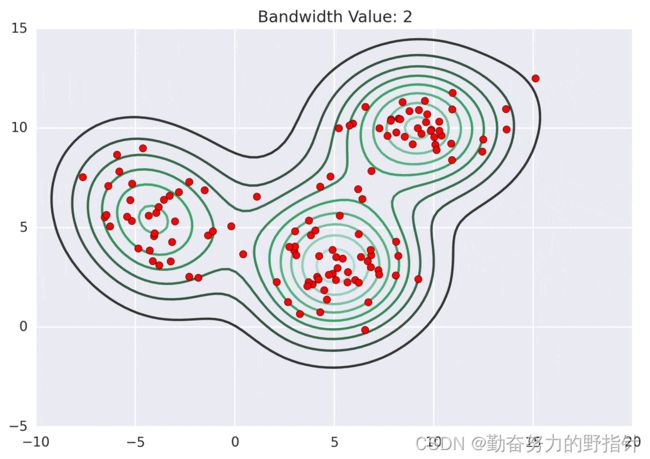
# -*- coding:utf-8 -*-
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift, estimate_bandwidth
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle ##python自带的迭代器模块
##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples=10000
##生产数据
X, _ = make_blobs(n_samples=n_samples, centers= centers, cluster_std=0.6,
random_state =0)
##带宽,也就是以某个点为核心时的搜索半径
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
##设置均值偏移函数
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
##训练数据
ms.fit(X)
##每个点的标签
labels = ms.labels_
print(labels)
##簇中心的点的集合
cluster_centers = ms.cluster_centers_
print('cluster_centers:',cluster_centers)
##总共的标签分类
labels_unique = np.unique(labels)
##聚簇的个数,即分类的个数
n_clusters_ = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters_)
##绘图
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
##根据lables中的值是否等于k,重新组成一个True、False的数组
my_members = labels == k
cluster_center = cluster_centers[k]
##X[my_members, 0] 取出my_members对应位置为True的值的横坐标
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
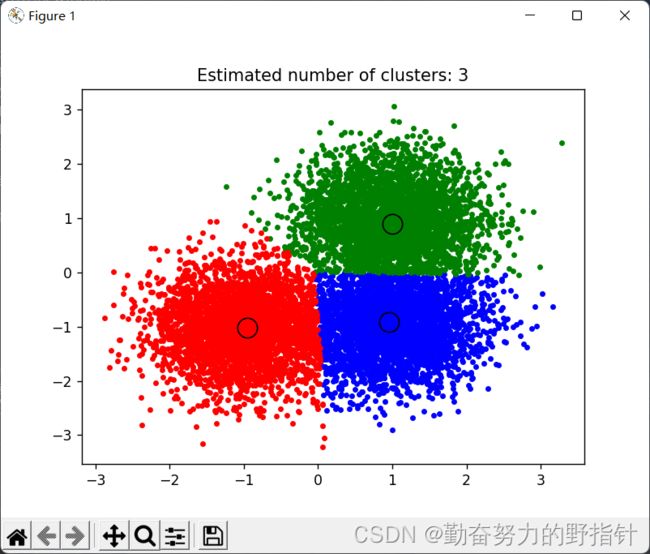
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
[1 1 1 ... 2 0 0]
cluster_centers: [[ 0.95599367 -0.91612234]
[ 0.99957414 0.89275465]
[-0.95425416 -1.01960393]]
number of estimated clusters : 3
DBSCAN算法
示例1
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle ##python自带的迭代器模块
from sklearn.preprocessing import StandardScaler
##产生随机数据的中心
centers = [[1, 1], [-1, -1], [1, -1]]
##产生的数据个数
n_samples = 750
##生产数据:此实验结果受cluster_std的影响,或者说受eps 和cluster_std差值影响
X, lables_true = make_blobs(n_samples=n_samples, centers=centers, cluster_std=0.4,
random_state=0)
##设置分层聚类函数
db = DBSCAN(eps=0.3, min_samples=10)
##训练数据
db.fit(X)
##初始化一个全是False的bool类型的数组
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
'''
这里是关键点(针对这行代码:xy = X[class_member_mask & ~core_samples_mask]):
db.core_sample_indices_ 表示的是某个点在寻找核心点集合的过程中暂时被标为噪声点的点(即周围点
小于min_samples),并不是最终的噪声点。在对核心点进行联通的过程中,这部分点会被进行重新归类(即标签
并不会是表示噪声点的-1),也可也这样理解,这些点不适合做核心点,但是会被包含在某个核心点的范围之内
'''
core_samples_mask[db.core_sample_indices_] = True
##每个数据的分类
lables = db.labels_
##分类个数:lables中包含-1,表示噪声点
n_clusters_ = len(np.unique(lables)) - (1 if -1 in lables else 0)
##绘图
unique_labels = set(lables)
'''
1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
2)plt.cm 一个颜色映射模块
3)生成的每个colors包含4个值,分别是rgba
4)其实这行代码的意思就是生成4个可以和光谱对应的颜色值
'''
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
plt.figure(1)
plt.clf()
for k, col in zip(unique_labels, colors):
##-1表示噪声点,这里的k表示黑色
if k == -1:
col = 'k'
##生成一个True、False数组,lables == k 的设置成True
class_member_mask = (lables == k)
##两个数组做&运算,找出即是核心点又等于分类k的值 markeredgecolor='k',
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col, markersize=14)
'''
1)~优先级最高,按位对core_samples_mask 求反,求出的是噪音点的位置
2)& 于运算之后,求出虽然刚开始是噪音点的位置,但是重新归类却属于k的点
3)对核心分类之后进行的扩展
'''
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', c=col, markersize=6)
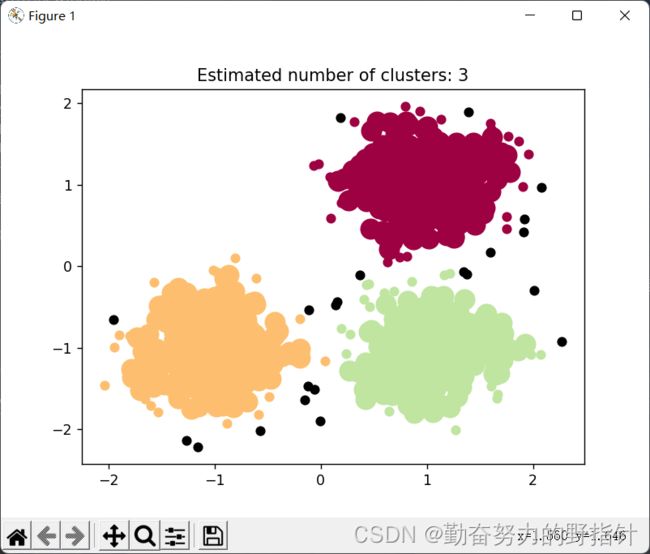
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
示例2
from sklearn import datasets
import numpy as np
import random
import matplotlib.pyplot as plt
import time
import copy
def find_neighbor(j, x, eps):
N = list()
for i in range(x.shape[0]):
temp = np.sqrt(np.sum(np.square(x[j] - x[i]))) # 计算欧式距离
if temp <= eps:
N.append(i)
return set(N)
def DBSCAN(X, eps, min_Pts):
k = -1
neighbor_list = [] # 用来保存每个数据的邻域
omega_list = [] # 核心对象集合
gama = set([x for x in range(len(X))]) # 初始时将所有点标记为未访问
cluster = [-1 for _ in range(len(X))] # 聚类
for i in range(len(X)):
neighbor_list.append(find_neighbor(i, X, eps))
if len(neighbor_list[-1]) >= min_Pts:
omega_list.append(i) # 将样本加入核心对象集合
omega_list = set(omega_list) # 转化为集合便于操作
while len(omega_list) > 0:
gama_old = copy.deepcopy(gama)
j = random.choice(list(omega_list)) # 随机选取一个核心对象
k = k + 1
Q = list()
Q.append(j)
gama.remove(j)
while len(Q) > 0:
q = Q[0]
Q.remove(q)
if len(neighbor_list[q]) >= min_Pts:
delta = neighbor_list[q] & gama
deltalist = list(delta)
for i in range(len(delta)):
Q.append(deltalist[i])
gama = gama - delta
Ck = gama_old - gama
Cklist = list(Ck)
for i in range(len(Ck)):
cluster[Cklist[i]] = k
omega_list = omega_list - Ck
return cluster
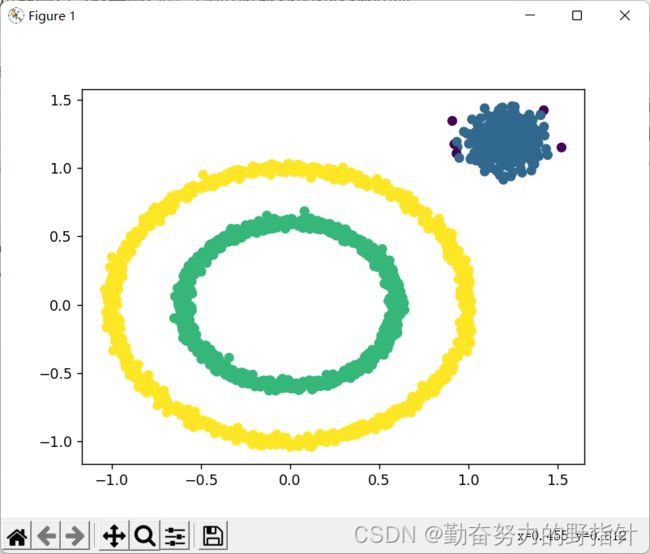
X1, y1 = datasets.make_circles(n_samples=2000, factor=.6, noise=.02)
X2, y2 = datasets.make_blobs(n_samples=400, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[.1]], random_state=9)
X = np.concatenate((X1, X2))
eps = 0.08
min_Pts = 10
begin = time.time()
C = DBSCAN(X, eps, min_Pts)
end = time.time()
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=C)
plt.show()