《深度学习入门》第3章实战：手写数字识别

《深度学习入门》第3章实战：手写数字识别

---

前言

笔者最近阅读了《深度学习入门——基于Python的理论与实现》这本书的第三章，章节最后刚好有个手写数字识别的实战内容，于是就照着书本内容写了程序跑了一下，在此做个记录。

---

`

一、一点介绍

这个手写数字识别的小案例，采用的是3层神经网络来实现的。需要说明的是，在这个小案例中，神经网络还不具备“学习”的功能，在训练之前，我们会读入一个sample_weight.pkl文件，这个文件里面保存了已经学习好的神经网络的权重和偏置参数。

这个神经网络的结构大概如下：

输入层： 784个神经元
隐藏层1： 50个神经元
隐藏层2： 100个神经元
输出层： 10个神经元

**为什么输入层是784个神经元？**因为这对应于图像的大小28*28=784，输入的图像被展开成一个一维的数组，大小正好是784。
**为什么输出层是10个神经元？**因为“手写数字识别”的识别结果有0-9，这10种可能，所以对应了10个神经元。再者，输出层采用的激活函数是softmax，所以，如果输出层的第0个神经元的值是0.632，那就说明这个数字有63.2%的可能性是0。
隐藏层的神经元数量可以设置为任何值。

下面这个get_data()函数用来加载数据。flatten设置为true表示展开输入图像为一维数组（784维）；normalize设置为True表示将输入图像正规化到0-1。

def get_data():
    
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
    return x_test, t_test

下面这个函数init_network()，顾名思义，就是初始化网络。它会读入保存在sample_weight.pkl文件中的参数，从而初始化网络。

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

下面这两个函数sigmoid()和softmax()都是激活函数。

def sigmoid(a):
    return 1 / (1 + np.exp(-a))


def softmax(a):
    exp_a = np.exp(a)
    sum = np.sum(exp_a)
    y = exp_a / sum
    return y

下面这个函数predict(network, x)是用来预测。输入的network是神经网络的参数，输入的x是手写数字图像数据。输出的y是各个标签对应的概率。

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    return y

下面这部分代码主要做了如下几个工作：①读入数据；②初始化网络；③进行预测；④评估预测的准确度。
这里还采用了“批处理”的思想。批处理指的是同时打包多条数据进行预测，这样可以提高数据的处理效率。下面代码中的批数量是100，意味着每次有100张图片被送入网络中进行预测。

x, t = get_data()  # x是测试数据，t是测试标签
network = init_network()
batch_size = 100  # 批数量
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
    x_batch = x[i: i + batch_size]
    y_batch = predict(network, x_batch)  # 预测
    # 选出y中最大值所在的下标
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

二、完整代码

import pickle
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录中的文件而进行的设定
from dataset.mnist import load_mnist
from PIL import Image
import numpy as np


# 定义一个函数，用于显示图片
def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()


# # 加载数据。flatten设置为true表示展开输入图像为一维数组（784维）；normalize设置为True表示将输入图像正规化到0-1
# (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
# img = x_train[0]
# label = t_train[0]
# print(label)
# print(img.shape)
# img = img.reshape(28, 28)
# print(img.shape)
#
# img_show(img)


def get_data():
    # 加载数据。flatten设置为true表示展开输入图像为一维数组（784维）；normalize设置为True表示将输入图像正规化到0-1
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def sigmoid(a):
    return 1 / (1 + np.exp(-a))


def softmax(a):
    exp_a = np.exp(a)
    sum = np.sum(exp_a)
    y = exp_a / sum
    return y


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    return y


x, t = get_data()  # x是测试数据，t是测试标签
network = init_network()
batch_size = 100  # 批数量
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
    x_batch = x[i: i + batch_size]
    y_batch = predict(network, x_batch)  # 预测
    # 选出y中最大值所在的下标
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

程序运行结果：

三、导入数据集的一个小问题

本程序运行需要导入mnist数据集，我一开始照着书上敲下面这行代码，试着导入dataset包之后，程序却报错：

from dataset.mnist import load_mnist

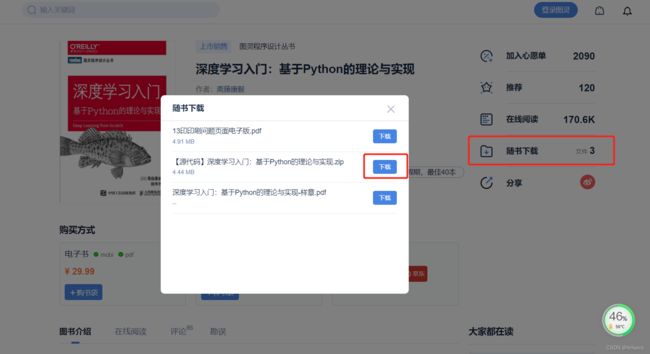
后来在网上搜索解决方案的时候才发现，mnist数据集需要到本书的官网资料上下载。官网链接：http://www.ituring.com.cn/book/1921
然后，先点击右侧的“随书下载”，再点击第二个“下载”。

下载好了之后，在dataset文件夹下找到mnist.py文件，把这个文件复制到项目venv\Lib\site-packages\dataset路径下。再次运行就不会报错了~