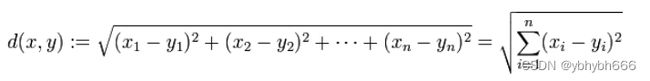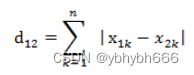k-means聚类(python代码)
k-means 聚类
接下来是进入聚类算法的的学习,聚类算法属于无监督学习,与分类算法这种有监督学习不同的是,聚类算法事先并不需要知道数据的类别标签,而只是根据数据特征去学习,找到相似数据的特征,然后把已知的数据集划分成几个不同的类别。
比如说我们有一堆树叶,对于分类问题来说,我们已经知道了过去的每一片树叶的类别。比如这个是枫树叶,那个是橡树叶,经过学习之后拿来一片新的叶子,你看了一眼,然后说这是枫树叶。而对于聚类问题,这里一堆树叶的具体类别你是不知道的,所以你只能学习,这个叶子是圆的,那个是五角星形的;这个边缘光滑,那个边缘有锯齿…… 这样你根据自己的判定,把一箱子树叶分成了几个小堆,但是这一堆到底是什么树叶你还是不知道的。
那么什么是k-means聚类呢
设我们的数据总共有 m 条,我们计划分为 3 个类别。如果我们的数据有两个特征维度,那我们的数据就分布在一个二维平面上,如果有十个维度,就分布在一个十维的空间中。
第一轮,先随机在这个空间中选取三个点,我们称之为中心点,当然选取的三个点不一定是实际的数据点。接着计算所有的点到这三个点的距离,这里的距离计算仍然使用的是欧氏距离,每个点(所有的点)都选择距离最近的那个作为自己的中心点。这个时候我们就已经把数据划分成了三个组。使用每个组的数据计算出这些数据的一个均值,使用这个均值作为下一轮迭代的中心点。
后面若干轮重复上面的过程进行迭代,当达到一些条件,比如说规定的轮次或者中心点的变动很小等,就可以停止运行了。
根据以上描述,我们大致可以猜测到实现kmeans算法的主要四点:
- (1)簇个数 k 的选择
- (2)各个样本点到“簇中心”的距离
- (3)根据新划分的簇,更新“簇中心”
- (4)重复上述2、3过程,直至"簇中心"没有移动
1.那么如何确定K值呢
有一个比较常用的方法,叫作手肘法。就是去循环尝试 K 值,计算在不同的 K 值情况下,所有数据的损失,即用每一个数据点到中心点的距离之和计算平均距离。
可以想到,当 K=1 的时候,这个距离和肯定是最大的;当 K=m 的时候,每个点也是自己的中心点,这个时候全局的距离和是 0,平均距离也是 0,当然我们不可能设置成 K=m。
而在逐渐加大 K 的过程中,会有一个点,使这个平均距离发生急剧的变化,如果把这距离与 K 的关系画出来,就可以看到一个拐点,也就是我们说的手肘。
如下图,我在这里虚拟了一份数据,可以看到在 K=4 的时候就是我们的肘点,在这个肘点前平均距离下降迅速,在 4 之后平均距离下降变得缓慢。但是这个方法只能适用 K 值不那么大的情况,如果 K 值较大,如几千几万,那迭代的次数就太多了,当然你也可以选择一个比较大的学习率来加以改进。不过总体而言,需要消耗一定的时间。
2.距离度量
将对象点分到距离聚类中心最近的那个簇中需要最近邻的度量策略,在欧式空间中采用的是欧式距离,在处理文档中采用的是余弦相似度函数,有时候也采用曼哈顿距离作为度量,不同的情况实用的度量公式是不同的。
2.1.欧式距离
2.2.曼哈顿距离
2.3.余弦相似度
算法优缺点
优点
- 简洁明了,计算复杂度低。 K-means 的原理非常容易理解,整个计算过程与数学推理也不是很困难。
- 收敛速度较快。 通常经过几个轮次的迭代之后就可以获得还不错的效果。
缺点
- 结果不稳定。 由于初始值随机设定,以及数据的分布情况,每次学习的结果往往会有一些差异。
- 无法解决样本不均衡的问题。 对于类别数据量差距较大的情况无法进行判断。
- 容易收敛到局部最优解。 在局部最优解的时候,迭代无法引起中心点的变化,迭代将结束。
- 受噪声影响较大。 如果存在一些噪声数据,会影响均值的计算,进而引起聚类的效果偏差。
python代码实现
这次我们使用的仍然是鸢尾花数据集,当然,由于是聚类,我们不需要使用标签数据,只需要使用特征数据就可以了。
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
'''
画出聚类后的图像
labels=聚类后的label,从0开始的数字
cents:质心坐标
n_cluster:聚类后簇的数量
color:每一簇的颜色
'''
def draw_result(train_x,labels,cents,title):
n=np.unique(labels).shape[0] #labels的不重复的列数
color=['red','orange','yellow']
plt.figure()
plt.title(title)
for i in range(n):
current_data= train_x[labels==i]
plt.scatter(current_data[:,0],current_data[:,1],c=color[i])
plt.scatter(cents[i,0],cents[i,1],c='blue',marker='*',s=100)
return plt
iris = datasets.load_iris()
iris_x=iris.data
clf=KMeans(n_clusters=3,max_iter=10,n_init=10,init='k-means++',algorithm='full',tol=1e-4,random_state=1)
clf.fit(iris_x)
print('SSE=',clf.inertia_)
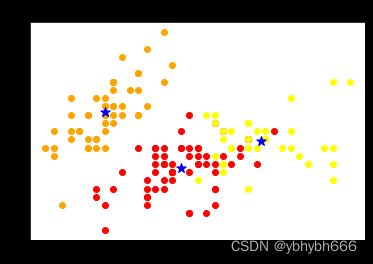
draw_result(iris_x,clf.labels_,clf.cluster_centers_,'kmeans').show()
通过运行上面的代码,会输出下面的这幅图像,当然,我们的鸢尾花数据集的属性有四个维度,这里输出的图像我们只使用了两个维度,但是仍然可以看出通过 K-means 计算出的中心点与数据分布基本上是一致的,而且效果也还不错。
k-means的衍生
K-means++
第一种是 K-means++,这种方法主要在初始选取中心点的时候进行了优化。原本第一轮是随机进行选取的,但是由于算法可能会陷入局部最优解,随机地选取可能引起结果的不稳定。 K-means++ 则是从已有的数据中随机地进行多次选取 K 个中心点,每次都计算这一次选中的中心点的距离,然后取一组最大的作为初始化中心点。
mini batch K-means
第二种 mini batch 方法,主要是基于在数据量和数据维度都特别大的情况下,针对运算变得异常缓慢的问题进行的改进。我们前面提到, K-means 的收敛速度相对较快,所以前面几步的变动比较大,到了后面的步骤其实只有非常小的变动。 mini batch 的方案就是在迭代时,不再使用所有的点,而是每个集合中选取一部分点进行计算,从而降低计算的复杂度。