tensorflow学习笔记：小项目实战：识别图中模糊的手写数字

识别图中模糊的手写数字

掌握东西最快的途径就是进行实践，通过项目来学习，不但能够给巩固所学内容，还可以让自己更好地熟悉项目的流程，总结提升自己。话不多说，这次来一个入门级别的实战项目：识别图中模糊的手写数字。
需要用到的数据集为开源数据集：MNIST
实现步骤：

• 导入MNIST数据集
• 分析MNIST样本特点，定义变量
• 构建模型
• 训练模型并输出中间状态参数
• 测试模型
• 保存模型
• 读取模型

1.1导入图片数据集

MNIST数据集官网：http://yann.lecun.com/exdb/mnist

MNIST数据集中的图片时28*28Pixel，所i，每一幅图都是1行784列的数据。tensorflow提供了一个库，可以直接用来自动下载与安装MNIST。(这里下载需要一会儿)

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

进入运行代码的目录下就可以看到目录下多出来要给MNIST_data文件夹，里面有四个gz文件：

• t10k-images-idx3-ubyte.gz
• t10k-labels-idx1-ubyte.gz
• train-images-idx3-ubyte.gz
• train-labels-idx1-ubyte.gz

接下来，将MNIDT中的一些信息打印出来观察一下，看看他的具体内容。

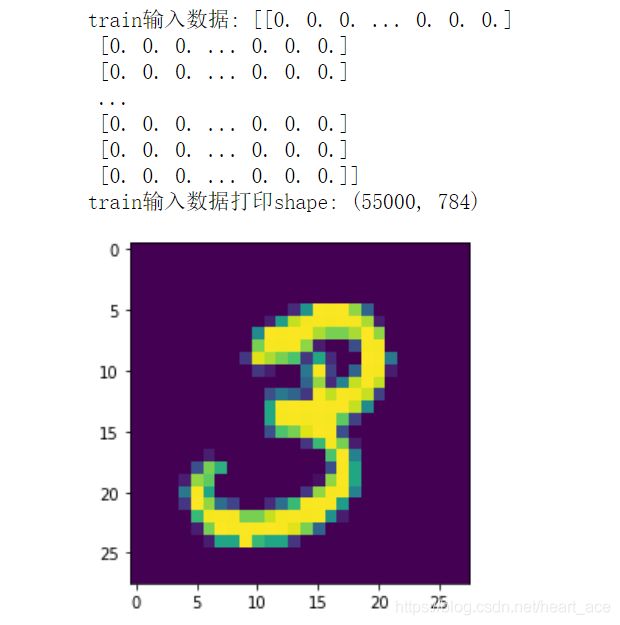
print ('train输入数据:',mnist.train.images)#输出训练集数据内容
print ('train输入数据打印shape:',mnist.train.images.shape)#训练集数据维度，得到结果为（55000，784），可以知道有55000张图片
import pylab 
%matplotlib inline

im = mnist.train.images[1]#取得位置为1的图片
im = im.reshape(-1,28)#将原本的1*784成定义为不定行的28列的数据
pylab.imshow(im)#加入显示图片
pylab.show()#显示图片

输出结果：

print ('test输入数据打印shape:',mnist.test.images.shape)#测试集数据
print ('validation输入数据打印shape:',mnist.validation.images.shape)#验证集数据

输出结果：
test输入数据打印shape: (10000, 784)
validation输入数据打印shape: (5000, 784)

我们还可以探索：

print("训练集中第2张图片的内容：",mnist.train.images[1])
print("训练集中第2张图片的标签：",mnist.train.labels[1])
print("训练集中第2张图片的内容的维度：",mnist.train.images[1].shape)
print("训练集中第2张图片的标签的维度：",mnist.train.labels[1].shape)

输出结果：略（因为内容太多不便于展示，请谅解）

可以看到train数据得维度为（55000，784），第一个数字为图片的索引，第二个数字为像素点索引。可以知道训练集中一共有55000张图片，每张图片的像素为784。第二幅图片对应的数字为3，标签(独热编码)表示为：[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]。

通过上面数据的输出可以了解到，MNIST包含三个数据集：

• 训练集（mnist.train）：用于进行训练
• 测试集（mnist.test）：用于评估训练过程中的准确度
• 验证集（mnist.validation）：用于评估最终模型的准确度

1.2分析图片的特点，定义变量

由于输入图片是一个55000*784的矩阵，所以线创建一个[None,784]的占位符x和一个[None,10]的占位符y，然后使用feed机制将图片和标签输入进去。这里维度中使用None的意思是：可变长度。

import tensorflow as tf

tf.reset_default_graph()#重置默认图，没有这一句也是没问题的，但是如果后面重复运行这一块代码就会报错
#定义占位符
x = tf.placeholder(tf.float32, [None, 784]) # mnist data维度 28*28=784
y = tf.placeholder(tf.float32, [None, 10]) # 0-9 数字=> 10 classes

1.3构建模型

样本构建完了，我们就可以构建模型了。

1.3.1定义学习参数

模型需要权重和偏置量，他们统一被叫做学习参数。我们可以通过Variable来声明学习参数，可以用于计算输入值，也可以在计算中被修改。

W = tf.Variable(tf.random_normal([784, 10]))#权重
b = tf.Variable(tf.zeros([10]))#偏置

在这里赋予tf.Variable不同的初值来创建不同的餐宿，一般将W设为一个随机值，b设为0.。需要注意的是：要考虑:$$y=W^T\ast X+b$$根据矩阵乘法的要求，结果需要是:$$(10，)=(784，10{)}^T\ast (784，)+(10,)$$

1.3.2定义输出节点

有了输入和模型参数，接着就可以将他们穿起来构建成真正的模型。

#构建模型
pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax分类

这样就构建好一个前向传播的结构，也就是说，只要模型中的参数合适，通过具体的数据输入，就能得到我们想要的分类。

1.3.3定义反向传播的结构

反向传播是编译训练模型，以得到合适的参数的过程。

# Minimize error using cross entropy
#交叉熵代价函数
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))

#参数设置
learning_rate = 0.01
# 使用梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

1.4训练模型并输出中间状态参数

这里开始真正训练模型，先定义训练相关参数。通过train_epochs代表要把整个训练样本迭代得次数，batch_size表示训练过程中一次抽取的数据样本个数，display_step表示每训练多少次进行显示。

epochs_list = []#存放训练次数
cost_list = []#损失值列表

training_epochs = 30#训练次数
batch_size = 100#单次样本数
display_step = 1#显示输出步长
saver = tf.train.Saver()#模型保存
model_path = "log/521model.ckpt"#保存路径
init = tf.global_variables_initializer()#变量初始化
# 启动session
with tf.Session() as sess:
    sess.run(init)#初始化变量
    # 启动循环开始训练
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples/batch_size)
        # 遍历全部数据集
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            # Run optimization op (backprop) and cost op (to get loss value)
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs,
                                                          y: batch_ys})
            # Compute average loss
            avg_cost += c / total_batch
            #将对应的数据加入到列表中去
            epochs_list.append(epoch+1)#这里加1是因为，epoch从0开始到24
            cost_list.append(avg_cost)
            
        # 显示训练中的详细信息
        if (epoch+1) % display_step == 0:
            print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))

    print( "Training Finished!")
    
    # 测试 model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # 计算准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print ("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))#嗲用测试集数据计算
    #eval表示运行这个张量

    # Save model weights to disk
    save_path = saver.save(sess, model_path)
    print("Model saved in file: %s" % save_path)

笔者训练后的输出结果：

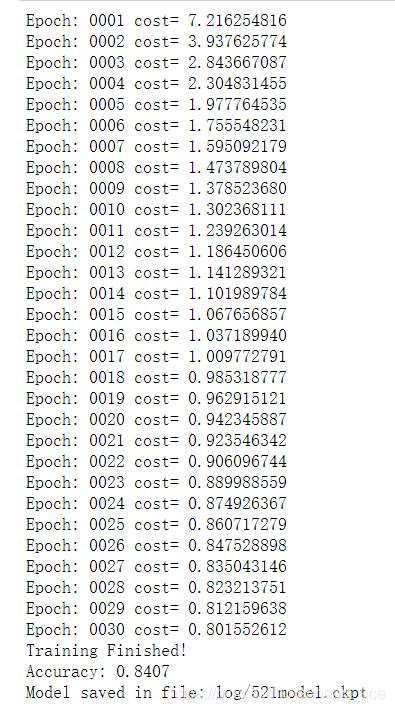
为了更加直观地看出损失值的变化情况，我们把信息可视化出来看俺：

%matplotlib inline
import matplotlib.pyplot as plt

plt.plot(epochs_list,cost_list,'.')
plt.title('训练次数与')
plt.xlabel('training epoch')
plt.ylabel('cost')

输出结果：

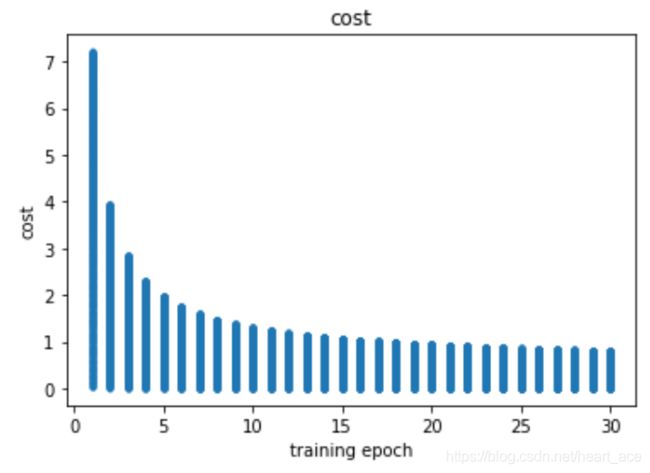
从图中可以看出损失值不断降低，通过30次训练后损失值降低到了0.80

1.5测试模型

测试错误率的算法是：直接判断预测的结果是否与真实的标签相同，如果相同就表明是正确的，如果不同就表示错误的，然后通过正确的个数除以总的个数，结果即为正确率。由于我们对标签进行了独热编码，所以需可以通过tf.argmax()访问到1所在位置，然后，再与目标进行比对。这里我测试出来的结果正确率为：84.07%。

测试正确率的算法与损失函数的算法略有不同，但是两者代表的意义很类似。需要注意的是：并不是所有模型的测试错误率和训练时最后一次损失值都很接近。
在上面的代码中我已经进行了输出，结果是这样的：

1.6保存模型

测试结束后，我们可以通过tf.train.Saver()将模型保存下来。最终在保存路径下得到以下文件：

• 521model.ckpt.data-00000-of-00001 ——模型中每一个参数的具体值
• 521model.ckpt.index ——模型中每一个参数的名字
• 521model.ckpt.meta —— 模型结构（图结构）
• checkpoint —— 模型信息（所有保存模型的历史记录【相对路径以及模型名称】）

1.7读取模型

把保存下来的模型读取进来应用一下。

#读取模型
print("Starting 2nd session...")
with tf.Session() as sess:
    # 初始化变量
    sess.run(tf.global_variables_initializer())
    # 读取模型
    saver.restore(sess, model_path)
    
     # 测试 model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # 计算准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print ("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
    
    output = tf.argmax(pred, 1)
    batch_xs, batch_ys = mnist.train.next_batch(2)
    outputval,predv = sess.run([output,pred], feed_dict={x: batch_xs})
    print(outputval)
    print(predv)
    print(batch_ys)
    
    #绘图
    im = batch_xs[0]
    im = im.reshape(-1,28)
    pylab.imshow(im)
    pylab.show()
    
    im = batch_xs[1]
    im = im.reshape(-1,28)
    pylab.imshow(im)
    pylab.show()

输出结果：


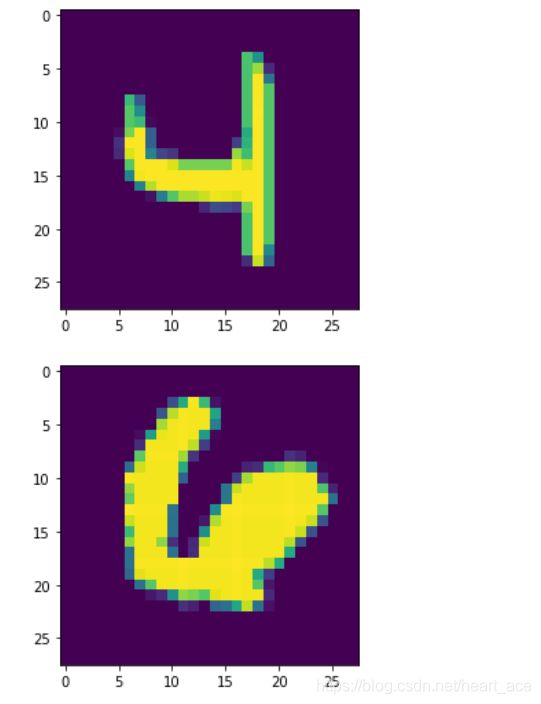
结果显示：测试集中得到的正确率为84.07%。下两张图片的结果为4和6，具体的数值为:

[1.2869774e-15 3.7685925e-16 1.6444707e-09 7.7209086e-11 1.0000000e+00 6.9272572e-13 2.3001670e-10 4.5443779e-12 3.0740577e-09 4.1590908e-08]

[2.9151161e-09 2.9765873e-14 1.6130567e-05 1.3727418e-13 1.4224457e-02 1.7260023e-10 9.8575759e-01 4.6236980e-08 9.0460768e-09 1.8503181e-06]

其中第一个数组的最大值的索引是4，第二个数组的最大值是6，所以表明预测结果是4和6.然后真正的结果为：[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]，[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]正好是4和6，说明这两张图被正确识别出来了。（多运行几次会遇到预测错的，毕竟我们训练出来的模型准确率没有达到100%嘛。）

OK，就到这儿吧！希望看完的小伙伴自己也实践一下，总结一下收获更大哦。（要是点个赞就更好了）
参考：李金洪老师的《深度学习之TensorFlow入门、原理与进阶实战》。