MLP概述

多层感知机概述

1. 线性过渡

我们在之前的内容中采用仿射变换，将输入对应于输出。但仿射变换中的线性是一个很强的假设。

1.1 线性模型将遇到的问题

线性模型默认一个特征对输出结果的影响是单调的，而这一假设于很多实际问题相矛盾。例如还款的可能性与收入的关系，收入从0增加到5万还款的可能性要远大于收入从100万增加到105万。（为了解决这一问题我们需要对数据进行处理，例如还款金额的对数作为特征。）再比如人体死亡可能性与人体温度的关系，人体温度高于37℃时，温度越高死亡可能性越大，而低于37℃时，温度越低死亡可能性越大。很明显，此时输出与输入特征不是线性关系。（解决办法：可以取输入温度与37℃度的距离作为特征值）。

但对于图像的世界来说，任何像素的重要性都以复杂的方式取决于该像素的上下文（周围像素的值）。这样我们的数据可能会有一种表示，这种表示会考虑到我们的特征之间的相互交互作用。**在此表示的基础上建立一个线性模型可能会是合适的！**但我们无法手动找到这种表示，所以我们采用深度神经网络，采用隐藏层进行表示，并采用线性预测器在该表示上建立线性模型。

1.2 从线性到非线性

我们可以通过合并一个或多个隐藏层来克服线性模型的限制，并处理更一般化的函数。要做到这一点，最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出。我们可以把前L-1层看作表示，把最后一层看作线性预测器。这种架构通常称为多层感知机（MLP）。

不难发现这两个层都是全连接的。每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。其公式可以表示如下：
$$\begin{gathered} \mathbf{H}=\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)} \\ \mathbf{O}=\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)} \end{gathered}$$
上面的隐藏单元由输入的仿射函数给出，而输出（softmax操作前）只是隐藏单元的仿射函数。我们直到仿射函数的仿射函数本身就是仿射函数，我们之前的线性模型已经可以表示所有的仿射函数了。所以，为了发挥结构层的潜力我们需要对每个隐藏单元应用非线性的激活函数。一般来说，有了激活函数，就不可能再将我们的多层感知机退化成线性模型：
$$\begin{gathered} \mathbf{H}=\sigma (\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}), \\ \mathbf{O}=\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}. \end{gathered}$$

2. 激活函数

激活函数是将输入信号转换为输出的可微运算。大多数激活函数都是非线性的，下面介绍一些常见的激活函数：

2.1 ReLU函数

ReLU函数提供了一种非常简单的非线性变换。给定元素$x$,ReLU函数被定义为该元素与0的最大值：
$$ReLU(x)=max(x,0)$$

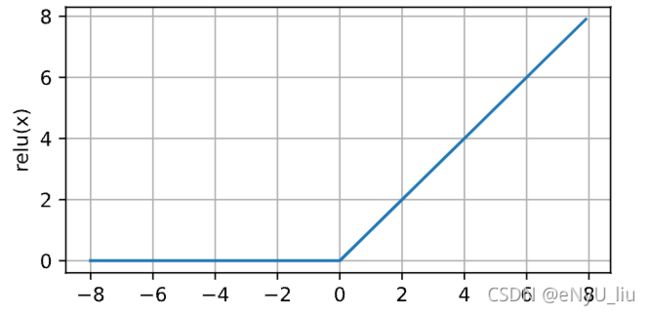
由图可见，当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。当输入精准为0时，ReLU函数不可导，在此时我们默认使用左侧的导数，即当输入为0时导数为0。我们可以忽略这种情况，因为输入可能永远不会是0。我们接下来绘制ReLU函数的导数。

代码为（y.backward()具体参数详见文档）：

# 向量对向量求导需要传递参数
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of relu',figsize=(5,2.5))

2.2 sigmoid函数

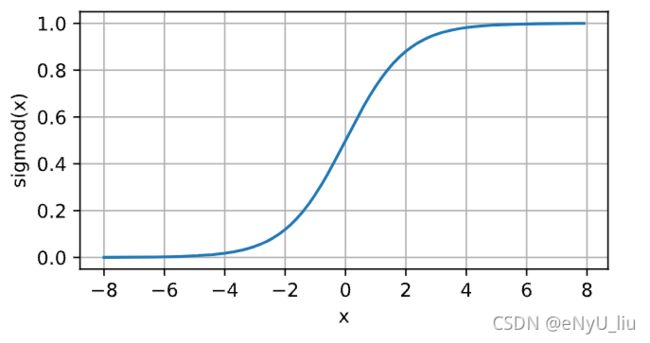
对于一个定义域在R中的输入，sigmoid函数将输入变换为区间（0，1）上的输出。
$$sigmoid(x)=\frac{1}{1+exp(-x)}$$
在最早的神经网络中，科学家们专注于阈值单元，即输入低于某个阈值时取值为0，反之取值为1。所以当人们的注意力转移至基于梯度的深度学习时，sigmoid函数是一个自然的选择，因为他是一个平滑的，可微的阈值单元近似。当我们想要将输出视作二分类问题的概率时，sigmoid仍然被广泛用作输出单元上的激活函数（可以将其视为softmax函数的特例）。然而sigmoid函数在隐藏层中已经较少使用，他在大部分时间被ReLU取代。

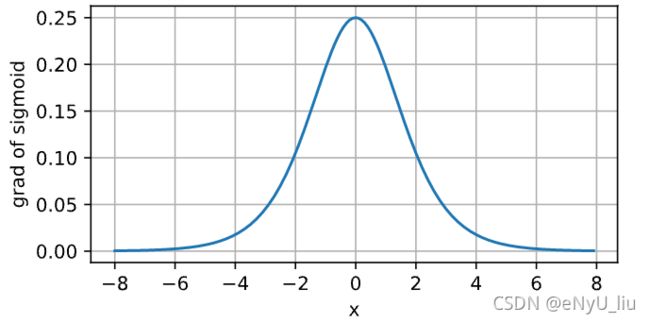
sigmoid函数导数图像如下：

# 清除以前的梯度！
x.grad.data.zero_()
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of sigmoid', figsize=(5,2.5))

注：将梯度置为0，x.grad.data.zero_()!!!

2.3 tanh函数

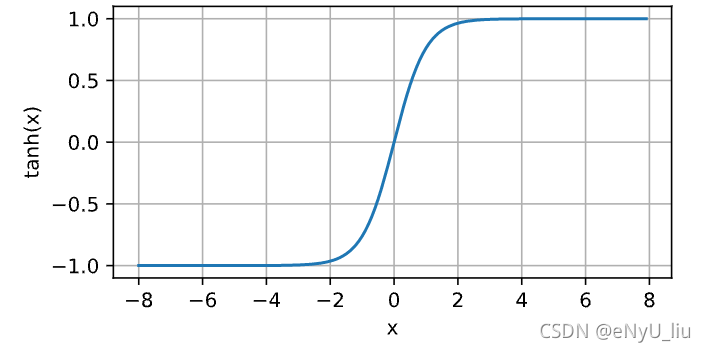
tanh激活函数与sigmoid函数类似，tanh(双曲正切函数)能将其输入压缩到区间（-1，1）上，其公式如下：
$$tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)}$$
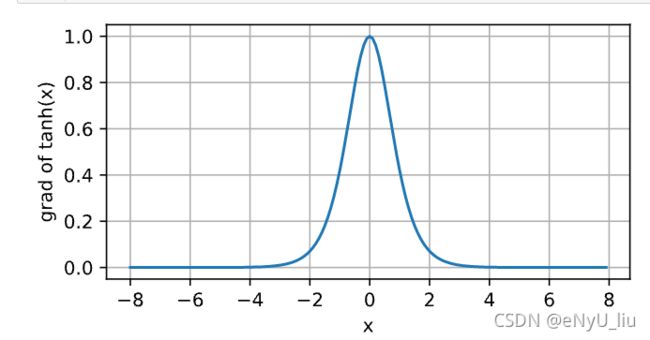
tanh函数图像及其导函数图像如下：