基于多元线性回归的股票分析与预测——R语言

一、数据来源

本文选取2016年12月至2021年12月共计5年贵州茅台股票的行情数据及后一天的开盘价格数据，对其进行实验研究。所有数据均来源于巨潮资讯网。

1.自变量

股票价格往往受到多个因素的影响，因此，需要建立包含多个变量的预测模型。对于模型的自变量，本文选取贵州茅台公布的行情数据中的最高价、最低价、收盘价、成交数、成交金额等行情指标， 以衡量该公司的股票行情。

2.因变量

由于股票价格包括开盘价、收盘价、最高价、最低价等价格,为了简化模型,本文选取贵州茅台公布行情是的后一天的开盘价格作为因变量。

二、多元线性回归

1. 初步建立多元线性回归模型

（1）数据集划分

将股票的历史数据通过csv文件输入 RStudio软件中，运用RStudio将贵州茅台5年来1200多条数据分为train.data（训练集）, test.data（测试集）两个数据集，每个数据集包含了600条数据集。其次将开盘价设为y，最高价设为x1，最低价设为x2，收盘价设为x3，成交量设为x4，成交金额设为x5。

### 从CSV文件中读取股票数据
data <- read.csv("600519 .csv", encoding = "UTF-8",sep = ",")
data<- data[3:8]
data
### 更改列名为"code", "date", "y", "x1", "x2", "x3", "x4", "x5"
colnames(data)
colnames(data)<-c("y", "x1", "x2", "x3", "x4", "x5")
data

### 训练集
train.data <- data[1:600,]
train.data

### 测试集
test.data <- data[600:1199,]
test.data

(2)建立回归模型

将train.data（训练集）代入多元线性回归模型，建立y（开盘价）与其他变量之间的回归方程。

### 用train.data数据集建立多元线性回归模型
lm.train <- lm(y~ x1+x2+x3+x4+x5,data = train.data)
lm.train
summary(lm.train)
### 对模型进行画图，并对模型进行验证和诊断
plot(lm.train)

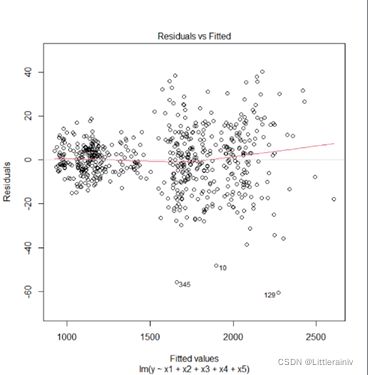
从残差图可以看出回归模型的残差存在一定的规律，在图中残差随着横坐标的变大而增大，说明回归模型存在方差异性，非线性关系明显，不满足线性关系。因此，该模型需要进一步优化。

接下来，从Normal Q-Q可以看出图上的散点基本沿着一条直线分布，这说明了回归模型残差正态性良好，满足了残差基本成正态分布的假设。

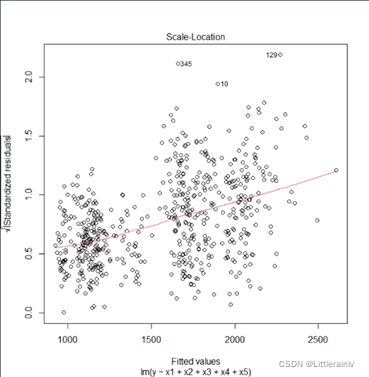
最后，从比例位置图可以看出散点呈明显规律，方差随横坐标增大而增大，则越往右的散点上下间距会越大，方差差异就越明显，也说明了回归模型不满足等方差性的假设。回归模型需要进一步改进。

2. 多元线性回归模型的优化

### 解决模型方差异性,对原始数据采取取对数的方式解决异方差性，重新建模
lny<- log(train.data$y)
lnx1<- log(train.data$x1)
lnx2<- log(train.data$x2)
lnx3<- log(train.data$x3)
lnx4<- log(train.data$x4)
lnx5<- log(train.data$x5)

lm.sol<-lm(lny ~ lnx1+lnx2+lnx3+lnx4+lnx5)
lm.sol
summary(lm.sol)
### 对重新建模的回归模型画图进行回归诊断
plot(lm.sol)

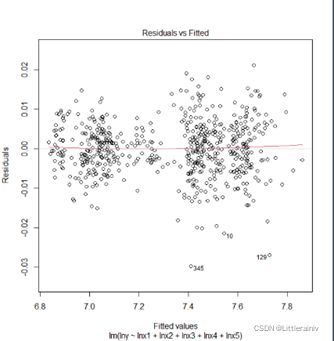
从残差图可以看出回归模型的残差随机分布，不存在规律，说明回归模型满足来了方差异性，线性关系明显。

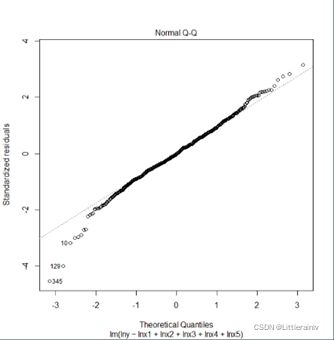
接下来，从Normal Q-Q可以看出图上的散点基本沿着一条直线分布，这说明了回归模型残差正态性良好，满足了残差基本成正态分布的假设。

最后，从比例位置图可以看出散点随机分布，没有呈明显规律，，方差差异不明显，说明了回归模型满足等方差性的假设。该模型对于预测茅台开盘价有明显的优势。

3.模型误差率

### 对模型进行预测并检验
test.data
lny<- log(test.data$y)
lnx1<- log(test.data$x1)
lnx2<- log(test.data$x2)
lnx3<- log(test.data$x3)
lnx4<- log(test.data$x4)
lnx5<- log(test.data$x5)

test.data <- data.frame(y=lny,
                        x1=lnx1,
                        x2=lnx2,
                        x3=lnx3,
                        x4=lnx4,
                        x5=lnx5)
test.data

test.data$pred <- predict(lm.sol,test.data)

### 用回归模型预测并计算误差率，其中误差率 =（实际值 - 预测值）/ 实际值。
test.data$diff <- (abs(test.data$y-test.data$pred)/test.data$y) * 100
test.data
summary(test.data)

最后，用回归模型预测并计算误差率，其中误差率 =（实际值 - 预测值）/ 实际值。在RStudio中将之前分好的数据集test.data取对数后代入到经过优化的回归模型中。

从图中可以看到最大diff（误差率）为0.68，平均diff（误差率）为0.08，最小diff（误差率）为0.0004。由此可知，模型的预测平均误差率在 0.08 左右，误差数值较实际值来说较小，由此得出模型的预测效果较好的结论。