【图像压缩】蚁群算法优化小波变换图像压缩【含Matlab源码 2177期】

⛄一、蚁群算法优化小波变换图像压缩简介

1 蚁群算法的基本模型和描述
Deneubourg等人提出了聚类基本模型 (Basic Model, BM) , 它的基本思想是:某一个体被捡起或在有更多同类的地方被放下的随机概率可用式 (1) 和式 (2) 表示.

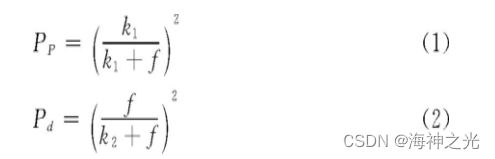
由公式可见, 被捡起的概率PP由k1、f决定, k1、k2是阈值, f是对象在蚂蚁的邻域内的接受度, 接受度f如果远小于阈值k1, 对象被捡起;接受度f如果远大于阈值k2, 对象被放下.

随后, Lumer等人将BM推广到数据聚类分析中, 提出LF算法[5].该算法所描述的平面上单个蚂蚁的行为和上面BM中所描述的单个蚂蚁行为相似, 但是它把随机数据对象投射到低维空间, 用概率转换函数计算对象捡起和放下概率, 同时蚂蚁在局部邻域范围内感知当前对象的集群相似性, 通过这个概率选择下一步动作是捡起还是放下.与BM思想的不同的是, LF扩展了判断数据聚类的范围, 更侧重于判断周围数据与蚂蚁背负的当前目标数据的相似性.

设定蚂蚁要找的物体集合是待进行聚类分析的数据集合N={Ni|Ni= (Ni1, Ni2, …, Nin) }, 那么相似性判断规则如式 (3) 、 (4) :

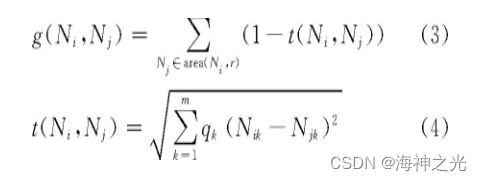
式中, g (Ni, Nj) 表示数据对象Ni和Nj的相似度, area (Ni, r) 表示数据对象Ni以r为半径的聚类区域, t (Ni, Nj) 表示Ni和Nj的加权欧氏距离.qk表示自适应加权参数, 用来动态调整聚类过程产生的作用.当g (Ni, Nj) =0时, 表示Ni和Nj的相似度最小, 当g (Ni, Nj) =1时, Ni和Nj的相似度最大, 即二者完全相同.

3 蚁群算法与分形图像压缩编码算法相结合
该算法分为三部分, 首先, 借助小波分析工具对原始图像分割并进行搜索空间构造, 利用分形几何的全局与局部的自相似性在小波变换的高层子图像内进行基本分形编码, 得到分类后的定义域块, 其中应用蚁群算法聚类形成数据样本空间, 其灰度值是通过所有域块取平均值组成.

其次, 进行定义域块与值域块匹配概率的类内搜索.为了解决定义域块内的匹配概率不相等[7], 有的可以同多个值域块相匹配, 有的可能一次机会也没有的问题, 需要有效减少IFS编码时间, 同时必须设置相应的策略, 对值域块的匹配进行优化.具体通过判断定义域块和值域块之间的距离完成, 应用阈值化法, 如果定义域块和值域块之间的距离在设定的阈值门限范围内, 可以近似认为它们是相同的块.根据不动点稳定性原理, 如果压缩变换接近, 其不动点也接近, 所以小的变化不会引起分形编码重构时有重大变化.此外, 类内建立基于域块的位置匹配概率表, 当值域块进入类时, 记录它们的分形编码, 并更新匹配表顺序, 始终将前面的位置分配给大概率.

第三, 考虑一幅图像的不同区域其纹理特征有可能存在很大的差异, 同时结合人眼对某些频率分量不敏感的视觉特性, 不采用传统方法中统一划分正方形方块进行分形编码的思路, 应用不同形状的区域划分与不同方向上子图像的纹理信息相适应, 使需要编码的不同方向上子图像的纹理信息与采用的分形预测块更加匹配, 通过这种改进, 能够进一步提高图像恢复质量, 缩短编码时间.

具体实现需经过以下步骤:

(1) 多分辨率小波分析.对图像进行三级分解后的结果如图1所示, LHn为水平方向, HLn为垂直方向, HHn对应45°、135°斜线方向上的细节 (n=1, 2, 3, ) , LL3为低频分量.

图1 三层小波分解示意图

(2) 确定分类后的定义域块, 并对定义域块和值域块进行匹配搜索.首先对三级小波变换的高频子图像HL3、LH3、HH3进行分割, 运用蚁群聚类算法, 对数据样本空间进行分类, 按照前面匹配概率的类内搜索制定的原则, 在对值域块进入定义域块分类后并依据匹配概率表搜索之前, 先进行值域块判别, 判别值域块属于分类结果中的哪个类别.具体作法是, 设定一个阈值, 当定义域块和值域块之间的距离大于阈值时, 认为其属于不同类, 否则按相同类处理, 在计算匹配误差和变换系数时, 只对属于相同类别的定义域块和值域块来计算, 这样可以避免很多不必要的搜索, 使搜索效率提高;同时, 应用这个过程逐渐建立起对应每一个类的匹配概率表, 那么对后续值域块的匹配就可以限定在类内的匹配概率表中进行, 不需要每次搜索类内所有的块, 由此缩短大量的搜索时间.

(3) 具体编码方案按照图像分割后的高频与低频子带的特性不同采用不同的编码方式, 由于低频子带包含图像的大部分能量, 故而对低频子带采用离散余弦变换 (DCT) 编码, 使大部分的信息的图像得以保留.

(4) 分析图像中各子块的纹理信息, 对不同地区根据纹理特征不同分别采用不同大小的块形状进行分形预测编码.以256×256的8bit图 (图2) 为例进行实验, 通过计算发现, LH、HL、HH区域中, 其水平和垂直方向的相关性不相同, 在HH区域, 行相关长度和列的相关长度相似, 所以采用正方形划分区域;在HL区域, 通过计算发现, 其行相关长度大于图像的列相关长度, 图像以水平纹理结构为主, 可以使用4×2矩形分割定义域块和值域块;在LH区域, 行相关长度小于列相关长度, 图像主要是垂直纹理图像, 可以用矩形域块2×4的大小进行定义域块和值域块的分割;而对于其他部分以低频率为主的子图像, 其包含了图像的大部分能量, 仍然使用2×2的块分割, 采用不同形状的分块与不同纹理特征的区域进行匹配分形编码, 使信噪比得以提高.图3所示为值域块分割过程.

解码过程是编码过程的逆过程, 具体进行图像恢复时, 从低频子图像到高频子图像逐级恢复, 先恢复低分辨率子图, 再恢复高分辨率子图, 当匹配计算时, 只能在同一子带相同方向上进行匹配的算术解码.因为只有水平、垂直和对角方向, 不需要在整个定义域内搜索, 节约了解码时间.蚁群算法与分形两种方法的结合, 使平均匹配次数大大减少, 加快了分形编解码速度.

图2 原始图像

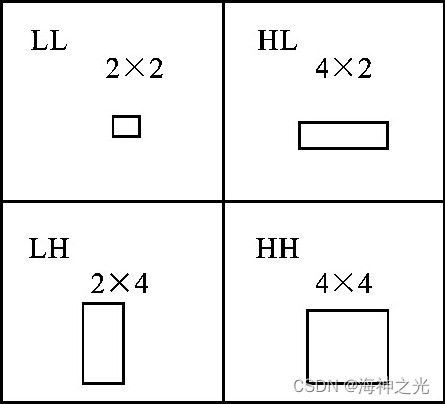
图3 值域块分割过程
解码过程是编码过程的逆过程, 具体进行图像恢复时, 从低频子图像到高频子图像逐级恢复, 先恢复低分辨率子图, 再恢复高分辨率子图, 当匹配计算时, 只能在同一子带相同方向上进行匹配的算术解码.因为只有水平、垂直和对角方向, 不需要在整个定义域内搜索, 节约了解码时间.蚁群算法与分形两种方法的结合, 使平均匹配次数大大减少, 加快了分形编解码速度.

⛄二、部分源代码

function denoise_PRL_2010_main
%

clear all; close all; clc;

% Load the ground truth image
img_truth = double(imread(‘barbara_truth.bmp’));

[nRow, nColumn] = size(img_truth);

% Use the ground truth image to generate the noisy image
noise_sig_truth = 10; % sigma_n used in the paper. This parameter is adjusted by the user.
noise_mu = 0;
img_noisy = img_truth + randn(size(img_truth)) .* noise_sig_truth + noise_mu;

% wavelet parameters
wbase = ‘Daubechies’;
mom = 8;
dwt_level = 5; %note that here, dwt_scale means the decomposition level of the DWT
[n,J] = func_quadlength(img_truth);
L = J-dwt_level;%here, L means the size of the coarsest level, 2^L

win_size = 2;
img_denoised = zeros(size(img_noisy));

% Since this is time consuming approach, divide the image into four parts, then
% conduct denoising for each part
for ii=1:4
win_size=2;

switch ii
    case 1
        img_denoised(1:end/2,1:end/2) = func_ACOShrink(img_noisy(1:end/2,1:end/2), wbase, mom, dwt_level, win_size);                        
    case 2
        img_denoised(end/2+1:end,1:end/2) = func_ACOShrink(img_noisy(end/2+1:end,1:end/2), wbase, mom, dwt_level, win_size);                        
    case 3
        img_denoised(1:end/2,end/2+1:end) = func_ACOShrink(img_noisy(1:end/2,end/2+1:end), wbase, mom, dwt_level, win_size);                        
    case 4
        img_denoised(end/2+1:end,end/2+1:end) = func_ACOShrink(img_noisy(end/2+1:end,end/2+1:end), wbase, mom, dwt_level, win_size);                        
end

end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 胡浩,张建林,李斌成,徐智勇.基于稀疏优化的图像压缩感知重建算法[J].半导体光电. 2021,42(02)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除