GhostNet

论文地址

---

前言

Ghostnet提出自己的架构设计思路：特征图的冗余是深度神经网络成功的一个重要特征。Ghostnet倾向于以一种代价低廉的线性操作来获取它们，而不是避免冗余的特性映射！

---

一、论文解读

1.Ghost卷积设计

在本文中，我们引入了一个新的Ghost模块，用更少的参数生成更多的特征。具体来说，将深度神经网络中的普通卷积层分为两部分。第一部分涉及普通的卷积，但它们的总数将被严格控制。给定第一部分的固有特征图，然后应用一系列简单的线性操作来生成更多的特征图。在不改变输出特征图大小的情况下，与普通卷积神经网络相比，Ghost模块所需的参数总数和计算复杂度都有所降低。实现过程如下：
首先通过主卷积生成基本特征图集合：X为输入特征图（尺寸参数为h：宽度,w：长度,c：通道数），f’为卷积层（尺寸参数为c:输入通道数，k:卷积核尺寸大小，m为输出通道数），X在与卷积层卷积后输出特征图集合Y’(尺寸参数为h’,w’,m)。此处省略了偏置参数。

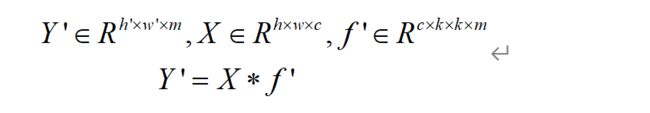
然后，对输出的基本特征图集合Y’做线性变化，以生成Ghost特征图。其中 fi是基本特征图集合Y’中第i个特征图, 是通过 生成的第j个Ghost特征图所做的线性变化，此处操作即指对应基本特征图集合中每个特征图通过线性操作生成s个Ghost特征图，最后一个线性操作为恒等映射以保留固有特征。

最后输出ms张特征图来作为最终输出特征图集合，相比于直接通过用ckkn（n=m*s）的卷积层做卷积，其计算量大幅减小（衰减比值大约为s）。整个特征图变化过程如下图：

2.Gbneck残差模块设计

此处作者参照Resnet的残差模块设计出Ghost瓶颈模块，ghost瓶颈主要由两个堆叠的ghost模块组成。第一个Ghost模块作为扩展层，增加通道的数量。我们把输出通道的数量与输入通道的数量之比称为扩展比。第二个Ghost模块减少通道数量以匹配捷径路径。然后在这两个Ghost模块的输入和输出之间连接快捷方式。每一层之后都使用批处理归一化(BN)和ReLU非线性。

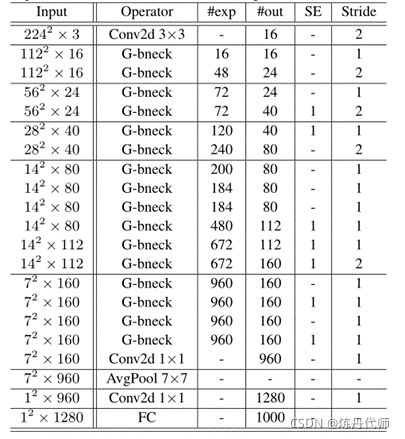
3.GhostNet网络架构

以本文之愚见，网络架构与残差模块设计基本是延续前人的思想，Ghostnet最重要的创新点在于卷积的设计（确实NB）！

二、代码实现

源代码比较恶心，嫖几行代码根本无法实现，貌似它把所有的操作都重写了一遍，对于我们这种想快速嫖代码的人来说就很难受了，没得办法，只有参考源代码自己写一个简单的出来了。前面说了最重要的创新是卷积模块的设计，那如果能嫖卷积模块的设计，剩下来的不都是之前论文实现的工作了吗？当然自己写出的代码还是不敢直接就用，还是对比下模型参数及计算量的好。经过验证，果然嫖代码能力天赋异禀的我完美实现了该网络。
各位同志如果要嫖作者大大的代码的话，先交个一键三连的学费，谢谢各位！

1.卷积模块

代码如下：

class Ghostconv(nn.Module):
    """Ghostnet的基础卷积模块"""
    def __init__(self,in_channels,out_channels):
        super(Ghostconv, self).__init__()
        main_channels=math.ceil(0.5*out_channels)
        #主卷积输出通道数
        cheap_channels=out_channels-main_channels
        #通过线性变化廉价操作得到的通道数
        self.piontconv1=nn.Sequential(nn.Conv2d(in_channels,main_channels,kernel_size=1,stride=1,bias=False),
                                      nn.BatchNorm2d(main_channels,eps=1e-5),
                                      nn.ReLU(inplace=True))
        self.linear_option=nn.Sequential(nn.Conv2d(main_channels,cheap_channels,kernel_size=3,padding=1,stride=1,groups=cheap_channels),
                                         nn.BatchNorm2d(cheap_channels,eps=1e-5),
                                         nn.ReLU(inplace=True))
        #线性操作通过深度可分离卷积实现，其中一半的特征图通过1*1卷积实现，一半的特征图由线性操作提供
    def forward(self,x):
        x=self.piontconv1(x)
        y=self.linear_option(x)
        return torch.cat((x,y),dim=1)

2.残差模块实现

代码如下（示例）：

class GhostUnit(nn.Module):
    """实现基本残差块和降维残差块"""
    def __init__(self,in_channels,out_channels,stride,use_se,ex_factor,k_size,padding):
        super(GhostUnit, self).__init__()
        # stride为2，3*3或5*5需要做下采样操作
        self.stride=stride
        self.use_se=use_se
        self.res=nn.Sequential()
        mid_channels=math.ceil(ex_factor*in_channels)
        # 主模块
        self.expconv=Ghostconv(in_channels,mid_channels)
        if stride==2:
            self.dwconv=nn.Sequential(nn.Conv2d(mid_channels,mid_channels,stride=stride,kernel_size=k_size,groups=mid_channels,bias=False,padding=padding),
                                      nn.BatchNorm2d(mid_channels,eps=1e-5),
                                      nn.ReLU(inplace=True))
            # 此处卷积核大小有两种可能：3或5
        if stride==2 or in_channels!=out_channels:
            self.res=nn.Sequential(nn.Conv2d(in_channels,in_channels,kernel_size=3,groups=in_channels,padding=1,stride=stride,bias=False),
                                   nn.BatchNorm2d(in_channels,eps=1e-5),
                                   nn.ReLU(inplace=True),
                                   nn.Conv2d(in_channels,out_channels,kernel_size=1,stride=1,bias=False),
                                   nn.BatchNorm2d(out_channels)
                                   )
            #此处不对1*1卷积的结果做激活操作
        self.pwconv=Ghostconv(mid_channels,out_channels)
        #SE模块
        if use_se==True:
            self.se=SElayer(4,mid_channels)
    def forward(self,x):
        residual=self.res(x)
        x=self.expconv(x)
        if self.stride==2:
            x=self.dwconv(x)
        if self.use_se:
            x=self.se(x)
        x=self.pwconv(x)
        return x+residual

3.网络实现

代码如下：

class Ghostnet(nn.Module):
    def __init__(self,num_calss,width_ratio=1):
        super(Ghostnet, self).__init__()
        self.inital=nn.Sequential(nn.Conv2d(in_channels=3,out_channels=int(16*width_ratio),kernel_size=3,padding=1,stride=2,bias=False),
                                  nn.BatchNorm2d(int(16*width_ratio)),
                                  nn.ReLU(inplace=True))
        self.block1=nn.Sequential(GhostUnit(in_channels=int(16*width_ratio),out_channels=int(16*width_ratio),stride=1,use_se=False,ex_factor=1,k_size=3,padding=1),
                                  GhostUnit(in_channels=int(16*width_ratio),out_channels=int(24*width_ratio),stride=2,use_se=False,ex_factor=3,k_size=3,padding=1))
        self.block2 = nn.Sequential(
            GhostUnit(in_channels=int(24*width_ratio), out_channels=int(24*width_ratio), stride=1, use_se=False, ex_factor=3, k_size=3, padding=1),
            GhostUnit(in_channels=int(24*width_ratio), out_channels=int(40*width_ratio), stride=2, use_se=True, ex_factor=3, k_size=5, padding=2))
        self.block3 = nn.Sequential(
            GhostUnit(in_channels=int(40*width_ratio), out_channels=int(40*width_ratio), stride=1, use_se=True, ex_factor=3, k_size=5, padding=2),
            GhostUnit(in_channels=int(40*width_ratio), out_channels=int(80*width_ratio), stride=2, use_se=False, ex_factor=6, k_size=3, padding=1))
        self.block4 = nn.Sequential(
            GhostUnit(in_channels=int(80*width_ratio), out_channels=int(80*width_ratio), stride=1, use_se=False, ex_factor=2.5, k_size=3, padding=1),
            GhostUnit(in_channels=int(80*width_ratio), out_channels=int(80*width_ratio), stride=1, use_se=False, ex_factor=2.3, k_size=3, padding=1),
            GhostUnit(in_channels=int(80*width_ratio), out_channels=int(80*width_ratio), stride=1, use_se=False, ex_factor=2.3, k_size=3, padding=1),
            GhostUnit(in_channels=int(80*width_ratio), out_channels=int(112*width_ratio), stride=1, use_se=True, ex_factor=6, k_size=3, padding=1),
            GhostUnit(in_channels=int(112*width_ratio), out_channels=int(112*width_ratio), stride=1, use_se=True, ex_factor=6, k_size=3, padding=1),
            GhostUnit(in_channels=int(112*width_ratio), out_channels=int(160*width_ratio), stride=2, use_se=True, ex_factor=6, k_size=5, padding=2),
        )
        self.block5 = nn.Sequential(
            GhostUnit(in_channels=int(160*width_ratio), out_channels=int(160*width_ratio), stride=1, use_se=False, ex_factor=6, k_size=5, padding=2),
            GhostUnit(in_channels=int(160*width_ratio), out_channels=int(160*width_ratio), stride=1, use_se=True, ex_factor=6, k_size=5, padding=2),
            GhostUnit(in_channels=int(160*width_ratio), out_channels=int(160*width_ratio), stride=1, use_se=False, ex_factor=6, k_size=5, padding=2),
            GhostUnit(in_channels=int(160*width_ratio), out_channels=int(160*width_ratio), stride=1, use_se=True, ex_factor=6, k_size=5, padding=2),
        )
        self.conv_last=nn.Sequential(nn.Conv2d(in_channels=int(160*width_ratio),out_channels=960,kernel_size=1,stride=1,bias=False),
                                  nn.BatchNorm2d(960),
                                  nn.ReLU(inplace=True))
        self.pool=nn.AdaptiveAvgPool2d(1)
        self.finally_conv=nn.Conv2d(in_channels=960,out_channels=1280,kernel_size=1,stride=1,bias=True)
        self.fc=nn.Linear(in_features=1280,out_features=num_calss)
    def forward(self,x):
        x=self.inital(x)
        x=self.block1(x)
        x=self.block2(x)
        x = self.block3(x)
        x = self.block4(x)
        x = self.block5(x)
        x=self.conv_last(x)
        x=self.pool(x)
        x=self.finally_conv(x)
        x=x.view(x.size(0),-1)
        x=self.fc(x)
        return F.softmax(x,dim=1)

三、验证模型

代码如下：

with torch.cuda.device(0):
  net = Ghostnet(1000,1)
  macs, params = get_model_complexity_info(net, (3, 224, 224), as_strings=True,
                                           print_per_layer_stat=True, verbose=True)
  print('{:<30}  {:<8}'.format('Computational complexity: ', macs))
  print('{:<30}  {:<8}'.format('Number of parameters: ', params))

原文中给出了模型的参数量和计算量，这不就可以验证一下模型有没有问题吗！

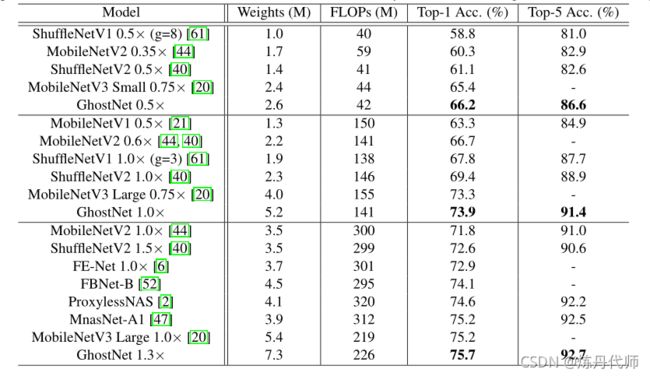
我模型跑出来的参数量（Weight）和计算量(FLOPs)如下：
1)当宽度因子取到0.5时：

这里和2.6M的Weight及42M的FLOPs相差无几！
2)当宽度因子取到1时：

这里和5.2M的Weight及142M的FLOPs差的一般！
总的来说：还行（此处省略一万只草泥马）！！！

总结

本文介绍了GhostNet的核心思想及其代码实现，以供大家交流讨论！
往期回顾：
（1）CBAM论文解读+CBAM-ResNeXt的Pytorch实现
（2）SENet论文解读及代码实例
（3）ShuffleNet-V1论文理解及代码复现
(4) ShuffleNet-V2论文理解及代码复现
下期预告：
EfficientNet论文阅读及代码实现