用隐马尔可夫模型推测女朋友心情(Ⅱ):求心情序列与事件序列的联合概率
上一期,王同学凭着自己对女友的了解,预估了 π \pi π、 A A A、 B B B,三个参数矩阵的取值。过去一周,通过与女友聊天,王同学了解到女友从周一到周日晚上做的事情分别为:看书、看剧、跑步、看书、看剧、逛商超、看剧。他想用这个观测序列预测女友这周的心情。
要预测女友的心情,换说话说,就是要求最大概率的心情序列,即,求某一心情序列,它与事件序列的联合概率最大。
循序渐进地解决问题,我们先考虑如何求心情序列与做事序列的联合概率,再考虑如何求最大概率。
假设王同学根据事件序列:{看书,看剧,跑步,看书,看剧,逛商超,看剧},凭直觉给出了女友的心情序列:{正常,正常,不开心,正常,开心,开心,正常},现在,如何求这两个序列的联合概率。
为表示方便,给出如下符号定义:
x i x_{i} xi:第i天的事件, i ∈ [ 1 , 7 ] i\in[1,7] i∈[1,7]。
y i y_{i} yi:第i天的心情, i ∈ [ 1 , 7 ] i\in[1,7] i∈[1,7]。
于是,上述序列的联合概率可表示为:
P ( [ y 1 , y 2 , y 3 , … , y 7 ] , [ x 1 , x 2 , x 3 , … , x 7 ] ) P([y_{1},y_{2},y_{3}, \dots,y_{7}], [x_{1},x_{2},x_{3}, \dots,x_{7}]) P([y1,y2,y3,…,y7],[x1,x2,x3,…,x7])
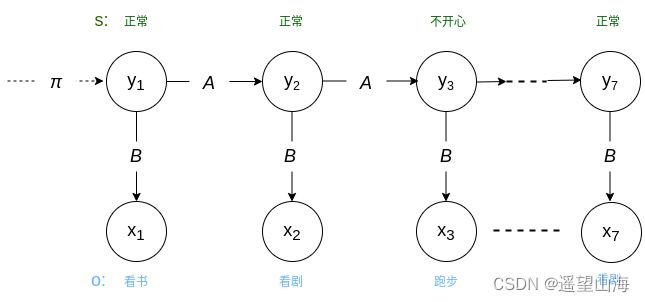
先来张示意图,直观感受一下:
图-1显示了每个时刻状态 y y y的取值和事件 x x x的取值。
为方便查询,将上一期的三张参数表也放这里。
表-1 初始状态概率分布 π
| 正常 | 开心 | 不开心 | |
|---|---|---|---|
| 0.7 | 0.2 | 0.1 |
表-2 状态转移概率分布 A
| 正常 | 开心 | 不开心 | |
|---|---|---|---|
| 正常 | 0.5 | 0.3 | 0.2 |
| 开心 | 0.4 | 0.5 | 0.1 |
| 不开心 | 0.6 | 0.1 | 0.3 |
表-3 发射概率分布 B
| 看书 | 逛商超 | 跑步 | 看剧 | |
|---|---|---|---|---|
| 正常 | 0.4 | 0.1 | 0.2 | 0.3 |
| 开心 | 0.2 | 0.5 | 0.1 | 0.2 |
| 不开心 | 0.1 | 0.1 | 0.6 | 0.2 |
现在,我们看着图-1来计算每个时刻的概率乘积。
(1) t = 1 t=1 t=1时,没有前驱状态,发生的概率由 π \pi π决定,即求 P ( y 1 = 正常 ) P(y_{1}=正常) P(y1=正常),查表-1得, P ( y 1 = 正常 ) = π 1 P(y_{1}=正常)=\pi_{1} P(y1=正常)=π1。当 { y 1 = 正常 } \{y_{1}=正常\} {y1=正常}时, { x 1 = 看书 } \{x_{1}=看书\} {x1=看书}的概率由发射概率矩阵 B B B决定。查表-3得, P ( x 1 = 看书 ∣ y 1 = 正常 ) = B 11 P(x_{1}=看书|y_{1}=正常)=B_{11} P(x1=看书∣y1=正常)=B11。所以, t = 1 t=1 t=1时的概率乘积为,
π 1 ⋅ B 11 \pi_{1} \cdot B_{11} π1⋅B11
(2) t = 2 t=2 t=2时,状态 y 2 y_{2} y2由前驱状态 y 1 y_{1} y1转移而来,其发生的概率由矩阵 A A A决定,查表-2得, P ( y 2 = 正常 ∣ y 1 = 正常 ) = A 11 P(y_{2}=正常|y_{1}=正常)=A_{11} P(y2=正常∣y1=正常)=A11。当 { y 2 = 正常 } \{y_{2}=正常\} {y2=正常}时, { x 2 = 看剧 } \{x_{2}=看剧\} {x2=看剧}的概率由发射概率矩阵 B B B决定。查表-3得, P ( x 2 = 看剧 ∣ y 2 = 正常 ) = B 14 P(x_{2}=看剧|y_{2}=正常)=B_{14} P(x2=看剧∣y2=正常)=B14。所以, t = 2 t=2 t=2时的概率乘积为,
A 11 ⋅ B 14 A_{11} \cdot B_{14} A11⋅B14
(3) 以此类推,得到其它时刻的概率乘积。
(4) 最后,可得7天的概率乘积,也就是心情序列和事件序列的联合概率,
P ( [ y 1 , y 2 , y 3 , … , y 7 ] , [ x 1 , x 2 , x 3 , … , x 7 ] ) = π 1 ⋅ B 11 ⋅ A 11 ⋅ B 14 ⋅ A 13 ⋅ B 33 ⋅ A 31 ⋅ B 11 ⋅ A 12 ⋅ B 24 ⋅ A 22 ⋅ B 22 ⋅ A 21 ⋅ B 14 \begin{equation} \begin{aligned} P([y_{1},y_{2},y_{3}, \dots,y_{7}], [x_{1},x_{2},x_{3}, \dots,x_{7}])=&\pi_{1} \cdot B_{11} \\ &\cdot A_{11} \cdot B_{14} \\ &\cdot A_{13} \cdot B_{33} \\&\cdot A_{31} \cdot B_{11} \\ &\cdot A_{12} \cdot B_{24} \\ &\cdot A_{22} \cdot B_{22} \\ &\cdot A_{21} \cdot B_{14} \end{aligned} \end{equation} P([y1,y2,y3,…,y7],[x1,x2,x3,…,x7])=π1⋅B11⋅A11⋅B14⋅A13⋅B33⋅A31⋅B11⋅A12⋅B24⋅A22⋅B22⋅A21⋅B14
由式(1)可以看出,联合概率=初始时刻的概率×每个时刻的状态转移概率×每个时刻的发射概率。
为表述方便,用向量 y \boldsymbol{y} y表示状态序列 { y 1 , y 2 , y 3 , … , y T } \{y_{1},y_{2},y_{3}, \dots,y_{T}\} {y1,y2,y3,…,yT},用向量 x \boldsymbol{x} x表示事件序列 { x 1 , x 2 , x 3 , … , x T } \{x_{1},x_{2},x_{3}, \dots,x_{T}\} {x1,x2,x3,…,xT},
由马尔可夫条件独立假设知,当前时刻的状态只与前一时刻状态相关,于是有,
P ( y ) = P ( y 1 ) ⋅ P ( y 2 ∣ y 1 ) ⋅ P ( y 3 ∣ y 2 ) … P ( y T ∣ y T − 1 ) = P ( y 1 ) ∏ t = 2 T P ( y t ∣ y t − 1 ) \begin{equation} \begin{aligned} P(\boldsymbol{y})&=P(y_{1}) \cdot P(y_{2}|y_{1})\cdot P(y_{3}|y_{2})\dots P(y_{T}|y_{T-1})\\&=P(y_{1})\prod_{t=2}^{T} P(y_{t}|y_{t-1}) \end{aligned} \end{equation} P(y)=P(y1)⋅P(y2∣y1)⋅P(y3∣y2)…P(yT∣yT−1)=P(y1)t=2∏TP(yt∣yt−1)
当给定 y \boldsymbol{y} y,对应事件序列发生的概率为: P ( x ∣ y ) = ∏ t = 1 T P ( x t ∣ y t ) P(\boldsymbol{x}|\boldsymbol{y})=\prod_{t=1}^{T} P(x_{t}|y_{t}) P(x∣y)=∏t=1TP(xt∣yt)。所以序列 y \boldsymbol{y} y与序列 x \boldsymbol{x} x的联合概率为:
P ( x , y ) = P ( y ) P ( x ∣ y ) = P ( y 1 ) ∏ t = 2 T P ( y t ∣ y t − 1 ) ∏ t = 1 T P ( x t ∣ y t ) \begin{equation} \begin{aligned} P(\boldsymbol{x},\boldsymbol{y})&=P(\boldsymbol{y})P(\boldsymbol{x}|\boldsymbol{y}) \\ &=P(y_{1})\prod_{t=2}^{T} P(y_{t}|y_{t-1})\prod_{t=1}^{T} P(x_{t}|y_{t}) \end{aligned} \end{equation} P(x,y)=P(y)P(x∣y)=P(y1)t=2∏TP(yt∣yt−1)t=1∏TP(xt∣yt)
将本例中状态转移概率和发射概率代入式(3),就可求得心情序列与事件序列的联合概率。
现在问题来了,心情有三种情况,七天的心情序列共有 3 7 3^{7} 37种情况。王同学想找到的是概率最大的那个序列。如果一个个试过去,太花时间了,下一期我们一起讨论更好的方法。