Auto-Encoders、VAE及实战
无监督学习
Why needed
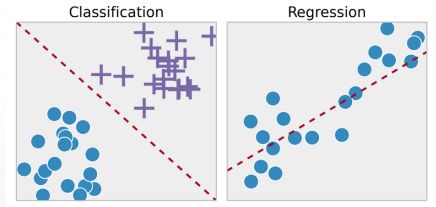
降维；预处理：巨大的尺寸，比如224x224，很难处理；可视化：https://projector.tensorflow.org/；利用无监督的数据；压缩、去噪、超分辨率
Auto-Encoders
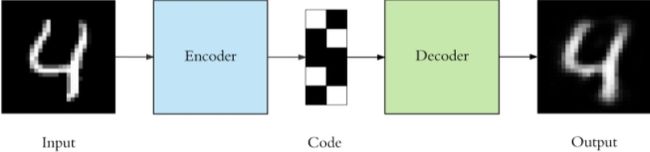
我们的目标就是重建他自己，最后一层重建节点784跟原来输入的节点一样。
特殊点：
1.输入和输出的维度一样，保证可以重建；
2.中间有个neck，可以升维也可以降维大部分是降维784=>2，降到两维时可以在二维向量表示，保留原有的信息；
Loss function
第一种（交叉熵）很适用，一张输入的图片上每个像素是0或1，x_ij = {0, 1}，其中x为输入，xhat为输出；
第二种(mean-square error, MSE)是输入输出两张那个图片每一个像素进行element-wise的运算，求导也相当方便。
Auto-Encoders的变种
-
Denoising AutoEncoders
-
Dropout AutoEncoder
当Dropout=0时，即全连接时，对应的Loss是最小的但是Accuracy不是最小的，即出现了overfitting的现象，因为把一些噪声也训练了；当Dropout有20%断掉时更加robust。
-
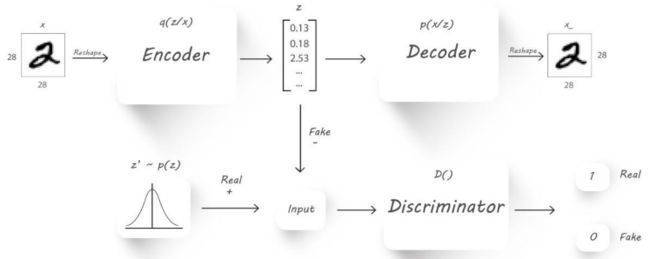
Adversarial AutoEncoders对抗式
-
Disribution of hidden code(x=>h=>xbar)
上述右边图片，横坐标为epoch，纵坐标为h的分布，随着training的进行，h的分部会越来越偏向负半轴，但人为的希望它的分布满足均值为0方差为某个值，虽然比较难达到，所以有以下措施； -
Give more details after GAN
使中间的hidden vector[0.13, 0.18, 2.53…]不仅能完成重建的工作，本来满足q分布~ q(z)，现在还能很好地符合我们想要的分布~p(z)，正好解决了刚才h的分部不均衡的问题。
-
变分自编码器
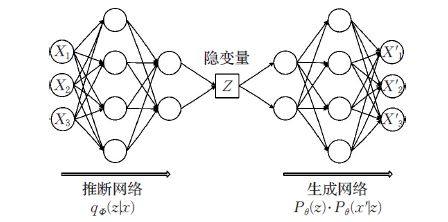
如上图所示，与自动编码器由编码器与解码器两部分构成相似，(Variational Auto-Encoders，VAE)利用两个神经网络建立两个概率密度分布模型：一个用于原始输入数据的变分推断，生成隐变量的变分概率分布，称为推断网络；另一个根据生成的隐变量变分概率分布，还原生成原始数据的近似概率分布，称为生成网络。
并且假设该过程产生隐变量Z ，即Z是决定X属性的神秘原因（特征）。其中可观测变量X 是一个高维空间的随机向量，不可观测变量 Z 是一个相对低维空间的随机向量。
尽管VAE 整体结构与自编码器AE 结构类似，但VAE 的作用原理和AE 的作用原理完全不同，VAE 的“编码器”和“解码器” 的输出都是受参数约束变量的概率密度分布，而不是某种特定的编码。
- 变分自编码器推导
变分自动编码器学习的是隐变量（特征）Z的概率分布，因此在给定输入数据X的情况下，变分自动编码器的推断网络输出的应该是Z的后验分布p(z|x) 。 但是这个p(z|x) 后验分布本身是不好求的。所以有学者就想出了使用另一个可伸缩的分布q(z|x) 来近似p(z|x)。通过深度网络来学习q(z|x) 的参数，一步步优化q使其与 p(z|x) 十分相似，就可以用它来对复杂的分布进行近似的推理。 - 要使 q(z) => p(z)，即min KL(q(z|x) || p(z|x))
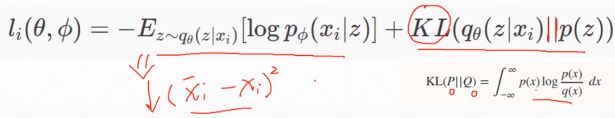
第一个目标为Autoencoder的重建误差足够小，意思就是若事先假设z本身的分布是服从高斯分布，这也就是要让推断网络（编码器）的输出也尽可能的服从高斯分布；第二个目标是隐藏的变量z 的分布q要逼近真实的分布p(z)。
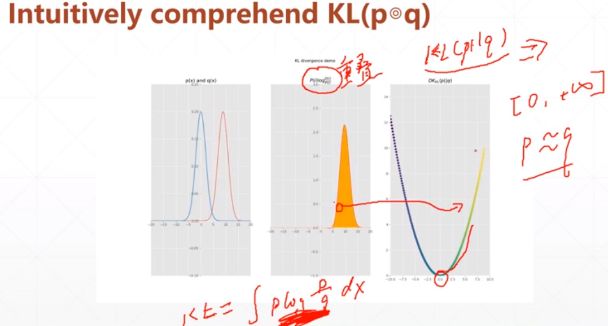
KL Divergence的示意图，第一幅图是p(x)和q(x)的正态分布图，第二张图是P(i)*log(Q(i)/P(i))，第三张图是KL散度的值。图二的面积不是图一中重叠部分的面积，而是两曲线比如红色曲线面积减去红色曲线下蓝色曲线的面积，意思是两部分分布概相减，即定义中log除法的含义。
当图一中两曲线重合时，图二面积为0，图三KL值此时为最小0。下图是KL散度的计算。
- Reparameterization trick
与在标准自编码器中直接输出隐状态值不同，VAE的编码器模型的输出描述的是每个维度分布。既然我们假设先验p(z)服从正态分布，我们将输出两个向量来描述隐状态分布的均值和方差。如果我们要构建一个真正的多元高斯模型，我们需要定义一个协方差矩阵来描述每个维度是如何相关的。但是，我们将做一个简化的假设，即我们的协方差矩阵只在对角线上有非零值，这允许我们用简单的向量来描述这些信息。
我们的解码器将通过从这些定义的分布中抽样来生成一个隐向量，并开始重建原始输入。
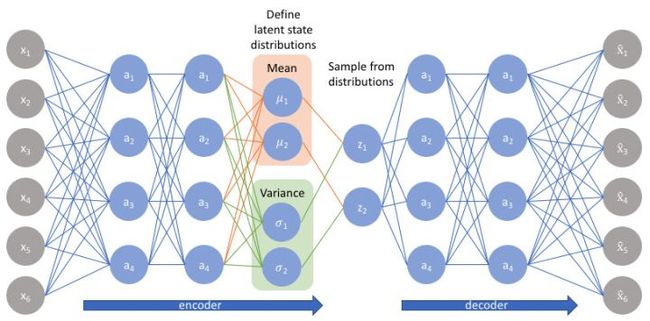
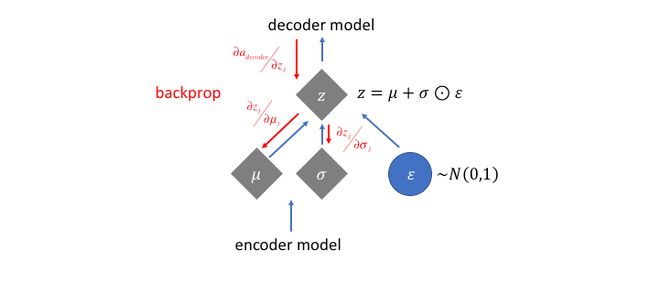
但是，这个抽样过程需要额外的关注。在训练模型时，我们使用反向传播来计算网络中每个参数与最终输出损失之间的关系。但是，我们无法为随机抽样过程做到这一点。幸运的是，我们可以利用一种称为“Reparameterization ”的聪明想法，即从单位高斯随机抽样ε，然后将随机抽样的ε乘以隐分布的均值μ，并用隐分布的方差σ对其进行缩放。
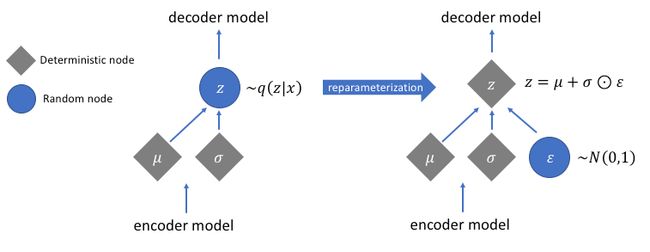
通过这种Reparameterization ，我们现在可以优化分布的参数，同时仍然保持从该分布随机采样的能力。
AE实战
AE
import torch
from torch import nn
class AE(nn.Module):
def __init__(self):
super(AE, self).__init__()
# [b, 784] => [b, 20]
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 20),
nn.ReLU()
)
# [b, 20] => [b, 784]
self.decoder = nn.Sequential(
nn.Linear(20, 64),
nn.ReLU(),
nn.Linear(64, 256),
nn.ReLU(),
nn.Linear(256, 784),
nn.Sigmoid()
)
def forward(self, x):
"""
:param x: [b, 1, 28, 28]
:return:
"""
batchsz = x.size(0)
# flatten
x = x.view(batchsz, 784)
# encoder
x = self.encoder(x)
# decoder
x = self.decoder(x)
# reshape
x = x.view(batchsz, 1, 28, 28)
return x, None
main
import torch
from torch.utils.data import DataLoader
from torch import nn, optim
from torchvision import transforms, datasets
from ae import AE
from vae import VAE
import visdom
def main():
mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)
mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
transforms.ToTensor()
]), download=True)
mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)
x, _ = iter(mnist_train).next()
print('x:', x.shape)
device = torch.device('cuda')
# model = AE().to(device)
model = VAE().to(device)
criteon = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
print(model)
viz = visdom.Visdom()
for epoch in range(1000):
for batchidx, (x, _) in enumerate(mnist_train):
# [b, 1, 28, 28]
x = x.to(device)
x_hat, kld = model(x)
loss = criteon(x_hat, x)
if kld is not None:
elbo = - loss - 1.0 * kld
loss = - elbo
# backprop
optimizer.zero_grad() # 梯度清零
loss.backward()
optimizer.step() # 梯度更新
print(epoch, 'loss:', loss.item(), 'kld:', kld.item())
x, _ = iter(mnist_test).next()
x = x.to(device)
with torch.no_grad():
x_hat, kld = model(x)
viz.images(x, nrow=8, win='x', opts=dict(title='x'))
viz.images(x_hat, nrow=8, win='x_hat', opts=dict(title='x_hat'))
if __name__ == '__main__':
main()
VAE
import torch
from torch import nn
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
# [b, 784] => [b, 20]
# u: [b, 10]
# sigma: [b, 10]
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 20),
nn.ReLU()
)
# [b, 20] => [b, 784]
self.decoder = nn.Sequential(
nn.Linear(10, 64),
nn.ReLU(),
nn.Linear(64, 256),
nn.ReLU(),
nn.Linear(256, 784),
nn.Sigmoid()
)
self.criteon = nn.MSELoss()
def forward(self, x):
"""
:param x: [b, 1, 28, 28]
:return:
"""
batchsz = x.size(0)
# flatten
x = x.view(batchsz, 784)
# encoder
# [b, 20], including mean and sigma
h_ = self.encoder(x)
# [b, 20] => [b, 10] and [b, 10]
mu, sigma = h_.chunk(2, dim=1) # 拆分
# reparametrize trick, epison~N(0, 1)
h = mu + sigma * torch.randn_like(sigma)
# decoder
x_hat = self.decoder(h)
# reshape
x_hat = x_hat.view(batchsz, 1, 28, 28)
kld = 0.5 * torch.sum(
torch.pow(mu, 2) +
torch.pow(sigma, 2) -
torch.log(1e-8 + torch.pow(sigma, 2)) - 1
) / (batchsz*28*28)
return x_hat, kld