2D姿态估计regression-based之RLE损失函数
参考:镜子,Indigo6
Heatmap-based
Heatmap-based方法通过显式地渲染高斯热图,让模型学习输出的目标分布,也可以看成模型单纯地在学习一种滤波方式,将输入图片滤波成为最终希望得到的高斯热图即可,这极大地简化了模型的学习难度,且非常契合卷积网络的特性(卷积本身就可以看成一种滤波),并且这种方式规定了学习的分布,相对于除了结果以外内部一切都是黑盒的Regression-based方法,对于各种情况(遮挡、动态模糊、截断等)要鲁棒得多。基于以上种种优点,Heatmap-based方法在姿态估计领域是处于主导地位的,SOTA方案也都是基于此,这也导致了一种学术研究与算法落地的割裂,你在各种数据集和比赛里指标刷得飞起,但项目落地时我们工程师却只能干着急,因为你用的方法又慢又吃内存,真实项目里根本没法用啊。
Regression-based方法则非常简单粗暴,直接监督模型学习坐标值,计算坐标值的L1或L2 loss。由于不需要渲染高斯热图,也不需要维持高分辨率,网络输出的特征图可以很小(比如14x14甚至7x7),拿Resnet-50来举例的话,FLOPs是Heatmap-based方法的两万分之一,这对于计算力较弱的设备(比如手机)是相当友好的,在实际的项目中,也更多地是采用这种方法。
说到Regression-based方法的优点,那是就是好呀就是好,可以简单总结为以下三点:
- 没有高分辨率热图,无负一身轻。计算成本和内存开销一起大幅降低。
- 输出为连续的,不用担心量化误差。(Heatmap-based输出的热图最大值点在哪,对应到原图的点也就确定了,输出热图的分辨率越小,这个点放大后对应回去就越不准。Regression-based输出为一个数值,小数点后可以有很多位,精度不受缩放影响)
- 可拓展性高。不论是one-stage还是two-stage,image-based还是video-based,2D还是3D,Regression-based方法都可以一把梭。此前就有用这种方法来将2D和3D数据放在一起联合训练的文章。这是Heatmap-based方法做不到的,因为输出是高度定制化的,2D输出必须渲染2D高斯热图,3D就必须渲染3D的高斯热图,计算量和内存开销也蹭蹭蹭地暴涨。
Regression-based
在完成配置后其实已经可以开始训练了,但是良好的工程习惯是应该先测试模型的导出部署和推理速度,确保这套流程能顺利进行且满足需求后再进行模型的训练。
- 原始的Regression方法精度最低
- 在加入了RLE方法后,Regression精度得到了一个较大的提升(PCKh上6个点)
- 不考虑计算效率的话,Heatmap方法在轻量模型上效果还是最好的,但是推理耗时是Regression的6倍
- 用Heatmap训练后的模型Backbone权重训练RLE,精度能再进一步提升(PCKh上1个点)
- 分辨率对于姿态估计任务非常重要,减小输入图片让Heatmap方法掉了8个点
- 另外不得不指出的一点,由于监督方式的不同,Heatmap方法由于降低了学习难度,梯度形式上的差距使得Heatmap在训练效率上是远高于Regression方法的
此时有两个思路:
-
轻量模型之所以弱于大模型,首先是参数量上存在差距。6倍的速度差距让我可以简单粗暴地增大Backbone参数量,比如将ShuffleNetV2的宽度系数从1.0变为2.0,推理速度也只是从6ms变成15ms,仍然比Heatmap快2倍。
-
使用Integral Pose Regression方法,学习隐式的Heatmap,有了更多可以引入监督信息的地方。
一、IPR
Integral Pose Regression方法由来已久,最早提出是为了解决Heatmap方法Argmax操作不可微分的问题,通过对网络输出的Heatmap计算Softmax归一化后求期望的形式得到坐标值。将Argmax软化为可微分的Soft-Argmax,进而实现了端到端训练,使得坐标值可以直接监督网络训练。监督方式上,IPR通过坐标值直接进行监督,采用L1或L2 Loss。
softmax的问题
一般来说,Softmax后计算期望,能够得到一个非常近似Argmax的值,这是一个很自然的过程,而且更妙的是,由于期望并不一定是整数,Soft-Argmax甚至能避开Argmax方法由于输出特征图尺寸过小带来的量化误差影响,这听上去很美好。
然而大家都知道的现实是Soft-Argmax方法虽然确实在小分辨率特征图输出上,能略胜Heatmap方法一筹,但一旦输出分辨率够高,性能就远远不如了。
本文揭示了Softmax的一个性质:倾向于让每一项的值都非零。简单来说,对于一个非常尖锐的分布(比如one-hot),Softmax会将其软化,变成一个渐变的分布,也就是说,原本取值为0的项,会被Softmax赋上一个非零的值,尽管这个值也许非常小,非常接近于0,但它是非零的。
那么,很自然地,输入特征图上响应值的大小,就会对Softmax的结果起到影响了,因为假如响应值是一个接近0的数字,那么Softmax之后的分布,原本为0的项,跟非0项的值会非常接近。
这个性质导致的结果是,最后计算得到的期望值会不准确。只有响应值足够大,分布足够尖锐的时候,期望值才接近Argmax结果,一旦响应值小,分布平缓,期望值会趋近于中心位置。
二、RLE—Human Pose Regression with Residual Log-likelihood Estimation(ICCV 2021 Oral
1. 核心思想
动机/背景: 近期研究指出直接坐标回归中 L1 Loss 比 L2 Loss 效果好,而 L1/L2 Loss 其实是从误差服从拉普拉斯/高斯分布的先验假设,通过极大似然估计(Maximum Likelihood Estimation, MLE)得到。那么如果能够学习到真实潜在的误差概率分布,这样得到的损失函数,是不是监督效果就应该更好呢?!
选择L2其实是一件很自然的事情,因为高斯分布具有大量优秀的特性:采样方便、解析的密度已知、KL距离容易计算,还有中心极限定理的保证——任何大的数据都趋近于高斯分布,所以你怎么用它几乎都是对的。但对于姿态估计任务而言,由于要精确地预测关键点位置,实际上概率分布是相对来说比较稀疏的,只有小部分区域具有概率,因此将拉普拉斯分布作为先验可能是一种更好的假设。
从这个视角来思考,我们其实可以把Heatmap-based方法看成是对模型的中间结果进行了 监督,显式地要求模型学习高斯概率分布,进而得出结果;而Regression-based方法由于缺少对概率分布的监督约束,模型内部学到的分布是不稳定的,完全受到训练数据的支配,因此在性能和鲁棒性上逊于Heatmap-based方法也就不难想象了。
方法:将训练过程中的所有误差作为标准化流(Normalizing Flows)生成模型的样本,使其学习将简单分布转换到“潜在误差分布”,并用学习到的“潜在误差分布”的极大似然估计作为损失函数
方法中比较难懂的点:
-
Flow生成模型是什么?
-
Flow生成模型怎么学习“将简单分布转换到潜在误差分布”的函数?
-
怎么利用 Flow 生成模型怎么计算“潜在误差分布”代表的损失?
论文设计:论文中不同 Designs 的核心目标就是设计更利于 Flow 生成模型学习的任务,即让它学习怎样的目标概率分布
2. 动机/背景
2.1 从高斯热图说起
众所周知,姿态估计分为坐标回归和热图回归两派。而热图回归中的热图一直以来都使用手工设计的 σ \sigma σ 二维独立高斯分布。例如假设输出热图 H H H 的分辨率为64×64,则 σ \sigma σ 为2,热图上某一位置 ( x , y ) (x, y) (x,y) 的值为
H i ( x , y ) = e − ( x − x i ) 2 + ( y − y i ) 2 2 σ 2 (1) H_i(x, y)=e^{-\frac{(x-x_i)^2+(y-y_i)^2}{2\sigma^2}}\tag{1} Hi(x,y)=e−2σ2(x−xi)2+(y−yi)2(1)
其中 μ = ( x i , y i ) \mu=(x_i, y_i) μ=(xi,yi) 是该输入图片中该关键点的一个真实坐标点。
2.2 坐标误差分布
假设 μ \mu μ 为特征点的groundtruth, μ ^ \hat{\mu} μ^ 为特征点回归的预测坐标(有的也会同时预测 σ ^ \hat{\sigma} σ^,代表误差分布的方差)。
误差服从正态分布(或样本服从正态分布),则最小二乘法就是极大似然估计
论文中提到之前有其它工作指出,使用拉普拉斯分布假设可以获得更好的性能,对应着L1损失函数。一个更接近真实误差分布的分布假设,应该能够有更好的性能。因此作者提出使用 flow-based generativate model 来学习潜在的误差分布。
2.3 似然函数和极大似然估计
似然函数
似然性(likelihood)与概率(possibility)同样可以表示事件发生的可能性大小,但是二者有着很大的区别:
- 概率 是在已知参数 θ \theta θ 的情况下,发生观测结果 x \boldsymbol{x} x 可能性大小;
- 似然性(似然函数) L ( θ ∣ x ) L(\theta|\boldsymbol{x}) L(θ∣x)则是从观测结果 x \boldsymbol{x} x 出发,分布函数的参数为 θ \theta θ 的可能性大小;
以下用 X \boldsymbol{X} X表示样本, x = ( x 1 , . . . , x n ) T \boldsymbol{x}=(x_1,...,x_n)^T x=(x1,...,xn)T表示样本点, f S ( x ; θ ) f_S(\boldsymbol{x};\theta) fS(x;θ)表示在样本 X \boldsymbol{X} X中随机取到 x \boldsymbol{x} x的概率值,即每个样本点的概率密度(概率)相乘,
f S ( x ; θ ) = { ∏ i = 1 n p ( x i ; θ ) ) ,当总体 X 为离散型随机变量时 ∏ i = 1 n f ( x i ; θ ) ) ,当总体 X 为连续型随机变量时 f_S(\boldsymbol{x};\theta)=\left\{\begin{matrix} \prod_{i=1}^{n} p(x_i;\theta)),当总体\boldsymbol{X}为离散型随机变量时 \\ \prod_{i=1}^{n} f(x_i;\theta)),当总体\boldsymbol{X}为连续型随机变量时 \end{matrix}\right. fS(x;θ)={∏i=1np(xi;θ)),当总体X为离散型随机变量时∏i=1nf(xi;θ)),当总体X为连续型随机变量时
极大似然估计法的提出是基于如下的想法:
当给定样本点 x \boldsymbol{x} x 时,可以令 L ( θ ; x ) = f S ( x ; θ ) L(\theta;\boldsymbol{x})=f_S(\boldsymbol{x};\theta) L(θ;x)=fS(x;θ) 为 θ \theta θ 的似然函数。对参数空间中两个不同参数 θ 1 \theta_1 θ1, θ 2 \theta_2 θ2 ϵ \epsilon ϵ Θ \Theta Θ ,如果有 f S ( x ; θ 1 ) f_S(\boldsymbol{x};\theta_1) fS(x;θ1) > f S ( x ; θ 2 ) f_S(\boldsymbol{x};\theta_2) fS(x;θ2),那么我们会认为样本点 x \boldsymbol{x} x 更“像是”来自总体 f S ( X ; θ 1 ) f_S(\boldsymbol{X};\theta_1) fS(X;θ1),即 θ 1 \theta_1 θ1 是比 θ 2 \theta_2 θ2 更有可能为总体样本 X \boldsymbol{X} X 的分布函数的参数。
极大似然估计
搞清楚了似然函数,就可以进阶到极大似然估计了。
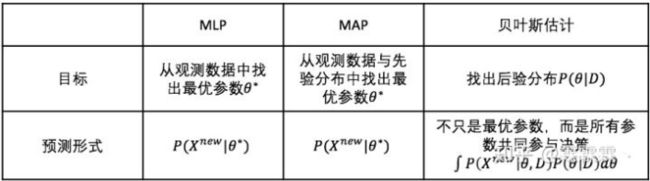
最大似然估计的思想在于,对于给定的观测数据 x \boldsymbol{x} x,我们希望能从所有的参数 θ \theta θ 中找出能最大概率生成观测数据 x \boldsymbol{x} x 的参数 θ ^ ( X ) \hat{\theta}(\boldsymbol{X}) θ^(X) ,作为参数 θ \theta θ 的极大似然估计量。
回到前面所说的似然函数,被估计出的参数 θ ^ \hat{\theta} θ^ 应该满足,其中最大化的步骤通过求导等于0来解得:
θ ^ ( X ) = a r g m a x ( l n L ( θ ^ ( x ) ; x ) \hat{\theta}(\boldsymbol{X}) = argmax(ln L(\hat{\theta}(\boldsymbol{x});\boldsymbol{x}) θ^(X)=argmax(lnL(θ^(x);x)
总结的来说对于一个未知参数的分布我们往往可以采用生成一批观测数据、通过这批观测数据做参数估计的做法来估计参数。最常用的有最大似然估计(MLE)、矩估计、最大后验估计(MAE)、贝叶斯估计等。
3. Flow生成模型
3.1 Generative Model
首先简单介绍一下生成模型,其目标是通过对分布中采样的样本点进行转换,训练一个生成器 G G G,将一个简单分布(如高斯分布) π ( z ) \pi(z) π(z)中的样本 z \boldsymbol{z} z 转换成复杂分布 p G ( x ) p_G(\boldsymbol{x}) pG(x) 中的样本 x \boldsymbol{x} x。如下图所示:

3.2 生成器G的训练过程
4. 论文的三种设计
4.1 Basic Design
我们将网络学习的目标,从让网络直接拟合目标分布,变成了拟合简单分布(本文使用拉普拉斯分布)+ 流模型变换调整(本文使用RealNVP)两个步骤,其中流模型中那一系列叠加的可逆变换可以通过叠加的FC层实现(本文使用3个具有64个神经元的全连接层)。

不足: 几乎每一次训练的简单分布 ( μ ^ , σ ^ ) (\hat{\mu}, \hat{\sigma}) (μ^,σ^) 都不同,每个人体的每一个特征点坐标的复杂分布也都不同。某一个复杂分布刚利用一个样本训练了从这种简单分布到自己的映射,结果下一次又换了一个简单分布,训练样本被分散了。
4.2 重参数化
学习 ϵ = μ − μ ^ σ ^ \epsilon = \frac{\mu - \hat{\mu}}{\hat{\sigma}} ϵ=σ^μ−μ^ 误差的潜在分布,训练时以每一个 ϵ \epsilon ϵ 为观察到的样本,基础分布设置为标准正态分布,训练时相当于利用重参数化技巧巧妙地实现 Basic Design 的目标,同时避开了 Basic Design 中训练样本被分散的问题。其中 x ˉ \bar{\boldsymbol{x}} xˉ 是真实目标分布。
不足: 这种设计相当于将训练过程中的所有误差作为样本,但是一开始坐标预测误差很大、Flow也刚开始训练,很可能Flow学到了错误的误差分布,而 Regressor 又采用了这种错误的误差分布(损失函数)作为指导,无法互相促进。
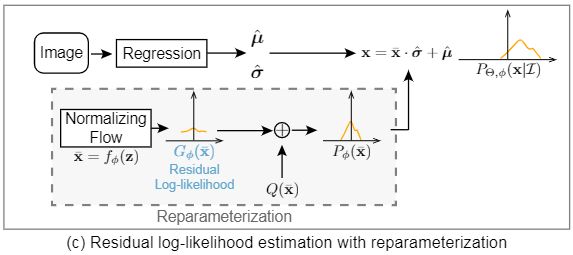
4.3 残差对数似然估计
要解决上面提到的模型依赖问题,本文设计了一条梯度shortcut来降低依赖程度。
用公式表示流模型拟合的目标分布, x ˉ \bar{\boldsymbol{x}} xˉ 是真实目标分布。可以构造拆分为三项:
l o g P o p t ( x ˉ ) = l o g ( Q ( x ˉ ) + l o g ( P o p t ( x ˉ ) s Q ( x ˉ ) ) + l o g s log P_{opt}(\bar{\boldsymbol{x}})=log(Q(\bar{\boldsymbol{x}})+log(\frac {P_{opt}(\bar{\boldsymbol{x}})} {s Q(\bar{\boldsymbol{x}})})+logs logPopt(xˉ)=log(Q(xˉ)+log(sQ(xˉ)Popt(xˉ))+logs
其中第一项Q(x)是一个简单分布(如高斯分布或拉普拉斯分布),第二项我们称之为残差对数似然项,第三项是一个常数s。
我们可以假设Q(x)是大致上接近于目标分布的,只是不够完美,这在之前我们已经有眉目了,选高斯分布不会错,选拉普拉斯分布更优。残差对数似然项是对第一项的一个补充,用于填补简单分布不够完美的部分,因此目标概率分布公式可以写成:
l o g P ϕ ( x ˉ ) = l o g Q ( x ˉ ) + l o g G ϕ ( x ˉ ) + l o g s log P_\phi(\bar{\boldsymbol{x}})=logQ(\bar{\boldsymbol{x}})+logG_\phi(\bar{\boldsymbol{x}})+logs logPϕ(xˉ)=logQ(xˉ)+logGϕ(xˉ)+logs
其中G(x)是流模型所需要学习的分布。经过这样的变换后,我们可以发现,回归模型对流模型的依赖被大大减轻了,因为不论流模型学到的结果如何,都只是在简单分布的基础上进行补充。这里的简单分布恰好正是我们前人使用的baseline,所以不管怎么学,我们的回归模型都不会太差,相反,随着流模型对 ( μ ^ , σ ^ ) (\hat{\mu}, \hat{\sigma}) (μ^,σ^) 的预测越来越准确,回归模型所拟合的分布将比baseline更加接近真实分布。
在4.2节的基础上,学习误差 ϵ = μ − μ ^ σ ^ \epsilon = \frac{\mu - \hat{\mu}}{\hat{\sigma}} ϵ=σ^μ−μ^ 的潜在分布与高斯分布的商 (Residual),训练样本和基础分布与4.2中一致。
从损失函数角度来看,其实就是加入了手工设计的L2损失函数项 ,其中 Q ( ϵ ) Q(\epsilon) Q(ϵ) 是标准正态分布:
L r l e = − l o g P ϕ ( ϵ ) + l o g ( σ ^ ) = − l o g Q ( ϵ ) − l o g G ϕ ( ϵ ) − l o g s + l o g ( σ ^ ) L_{rle}=-log P_\phi(\epsilon)+log(\hat{\sigma})=-logQ(\epsilon)-logG_\phi(\epsilon)-logs+log(\hat{\sigma}) Lrle=−logPϕ(ϵ)+log(σ^)=−logQ(ϵ)−logGϕ(ϵ)−logs+log(σ^)
而当训练结束,回归模型学到的 ( μ ^ , σ ^ ) (\hat{\mu}, \hat{\sigma}) (μ^,σ^) 就固定了,我们的流模型也固定了,由于我们假设所有的数据都服从我们的目标分布,变换函数是不会因为输入数据的变化而受影响的。更牛逼的是,由于是在N(0, I)的标准分布上进行的变换,在测试推理阶段,平移缩放系数直接就可以看成最终预测的坐标值。
因此在推理阶段我们就不再需要运行流模型了,我们的回归网络至此已经学到了流模型变换后的真实分布。这也是本文提出的方法的妙处所在,训练时对目标分布的假设就已经确定了,剩下的就又回到了Regression-based方法的既定流程上,确定分布假设,对应设计损失函数即可。