量子计算入门01-量子计算_夏培肃

引 言

​ Feynman于 1982年指出: 按照量子力学原则建 造的新型计算机对解某些问题可能比常规计算机更 有效 [1 ] .在此基础上 , 1985年 Deutsch指出利用量子态的相干叠加性 ( coherent superposition)可以实现 并行的量子计算. 1994年 Sho r提出大数因子分解 的量子算法 ,如果在量子计算机上计算 ,求一个 n 位大数的两个质因子所需的时间只是 n 的多项式;而 在常规计算机上计算 ,所需的时间则为O( 2 ^n /2 ) . 当 n 很大时 ,常规计算机变得无能为力 . 最近几年,有关量子计算的学术论文和报告已大 量发表,其中不乏介绍量子计算原理的 ,还出版 了若干专著 ,有些大学甚至在因特网上公布了他 们的量子计算课程讲义. 这些论文、报告、专著和 讲义主要是为在量子力学方面有一定基础的人写的, 其中的概念、术语和符号使计算机科技人员难以理解. 本文试图用计算机工作者所能接受的语言来介绍量子 计算的基本概念. 其实 ,对于那些只是想对量子计算 有一些初步了解的人来说 ,并不一定要去系统地学习 量子力学,只要了解和量子计算有关的量子态的基本 特性就可以了.这就如同了解常规计算机时 ,不一定需 要系统地学习半导体物理学. 和量子计算有关的量子 态的基本特性[ 36]是: 量子态的叠加 ( superposition)、 干涉 (interference)、纠缠 ( entanglement)和不可克 隆 ( nonclonability) . 比量子计算更广泛的是量子信息学 ( quantum information) ,但常常有人将量子信息学称为量子计 算 ,广义的量子计算除了计算以外 ,还包括量子通信 ( quantum communication )、 量 子 密码 ( quantum cryptography)、量子传态 ( quantum teleportation)、 量子密集编码 ( quantum dense coding )等 .

量子位

​ 在常规计算机中 ,信息单元用二进制的 1个位 来表示 ,它不是处于“ 0”态就是处于“ 1”态 . 在二进 制量子计算机中 ,信息单元称为量子位 ( qubit) , 它除了处于“ 0”态或“ 1”态外 ,还可处于叠加态 ( superposed state). 叠加态是“ 0”态和“ 1”态的任意线 性叠加 ,它既可以是“ 0”态又可以是“ 1”态 , “ 0”态和 “ 1”态各以一定的概率同时存在. 通过测量或与其 它物体发生相互作用而呈现出“ 0”态或 “ 1”态 .任何 两态的量子系统都可用来实现量子位 ,例如氢原子 中的电子的基态 ( ground state)和第 1激发态 ( first excited state)、质子自旋在任意方向的+ 1 /2分量 和- 1 /2分量、圆偏振光的左旋和右旋等.

​ 一个量子系统包含若干粒子 ,这些粒子按照量子力学的规律运动 ,称此系统处于态空间的某种量子态.态空间由多个本征态 (eigenstate) (即基本的量子态 )构成 ,基本量子态简称基本态 ( basic state ) 或基矢 ( basic vector) . 态空间可用Hilbert空间 (线性复向量空间 )来表述 ,即 Hilbert空间可以表 述量子系统的各种可能的量子态.

​ 为了便于表示和运算 , Dirac提出用符号|x〉来 表示量子态 ,|x〉是一个列向量 ,称为 ket;它的共轭 转置 (conjugate transpose) 用〈x|表示 ,〈x|是一个行向量 ,称为 bra .一个量子位的叠加态可用二维 Hilbert空间 (即二维复向量空间 )的单位向量|j〉来描述 ,其简化的示意图如图 所示 . 在这个空间里 ,|j〉 可写成:|j〉 = a|↑〉 + b|→〉， 式中|↑〉和|→〉是量子位的基本态 ,它们正交; a 和 b 为概率振幅 ( probability amplitude) ,它们是复 数;|a|^2 和|b|^2 分别表示|j〉为|↑〉态和|→〉 态的 概率 ,且|a|^2 + |b|^2 = 1,这表明|j〉是单位向量 ,也称|j〉是规一化的 (nomalized).在常规计算机中,一个数位的态是确定性的 (deterministic ) ,而在量子计算机中,量子位的叠加态不 是确定性的,而是概率性的 ( probabilistic) .

 当|j〉对|↑〉投影时 ,|j〉变成|j〉↑ ,   |j〉→ = b|→〉,  这相当于在|→〉方向对|j〉进行测量 ,例如对穿过垂直偏振光滤波器的偏振光进行观测 ,只能观测到水平偏振光 ,它出现的概率为|b|^2 . 所以 ,对处于叠加态的量子位进行观察或测量时 ,叠加态将受到干扰 ,并发生变化 ,这种变化称为坍缩. 对于上述测量 ,叠加态坍缩为基本态.

令|↑〉 = |0〉, |→〉 = |1〉,则|j〉 = a|0〉 + b|1〉. 令 x∈ { 0, 1},在二维 Hilbert空间 ,|x〉是具有 两个分量的向量. 令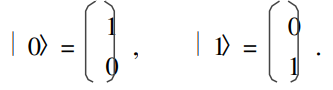 

​ 〈x|是|x〉的共轭 ,它是具有两个分量的行向量 ,即 〈0|= ( 1, 0) , 〈1|= ( 0, 1). 令 y∈ { 0, 1},则〈x|y 〉( = 〈x||y 〉)称为内积 ,它是 一个标量. 〈0|0〉 = 〈1|1〉 = 1, 〈0|1〉 = 〈1|0〉 = 0. |x〉〈y|称为外积 ,它是一个算符.

上式说明: |0〉〈0|作用在|j〉上是将其中属于|0〉的成分取出 ,也可以说|0〉〈0|使|j〉 对|0〉投影 ,即在|0〉方向测量|j〉. 同样 ,|1〉〈1|(|j〉)= b|1〉, |1〉〈1|使|j〉对|1〉投影 ,即在|1〉方向测量|j〉.

量子寄存器

​ n 个量子位的有序集合称为 n 位量子寄存器. 它的态是 n 个量子位的态的张量积 ( tensor product) . 张量积亦称直积,用符号 表示 ,它的表达式如下:

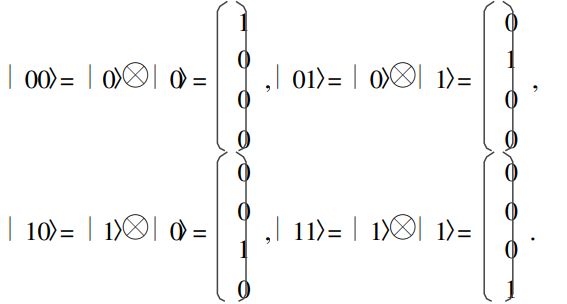​ 若 对于 2位量子寄存器 ,可得出: 假设一个 2位量子寄存器的每一位都处于|0〉, 则此寄存器的态为 若 |j0〉= a0|0〉+ b0|1〉, 则 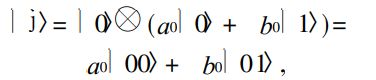式中 |a0|^2 + |b0|^2 = 1. 可以看出寄存器中的数可以为 00,也可以为 01,它们存在的概率分别为|a0|^2 和|b0|^2 . 若 |j1〉= a1|0〉 + b1|1〉, 则 寄存器中的数可以同时为 00, 01, 10, 11,它们存在 的概率分别为:: |a1a0|^2 ,|a1b0|^2 , |b1a0|^2 和 |b1b0|^2 . 也可以说 2位量子寄存器的叠加态|j〉是 2^2 维 Hilbert 空间的单位向量 ,它有 4个相互正交 的基本态: |00〉, |01〉, |10〉, |11〉.

​ 在量子计算机中 ,处于叠加态的 n位量子寄存 器中的数是从 0到 2^n - 1的所有的数 ,它们各以一 定的概率同时存在 . 在常规计算机中 , 1个 n位寄存 器只能保存 1个 n 位二进制数;而在量子计算机中 , 1个 n 位量子寄存器可以同时保存 2^n 个 n 位二进制数. 量子寄存器位数的线性增长使存储空间指数增长 ,这是量子计算机的一个基本特点.

​ 量子寄存器的态的测量可以通过测量寄存器中 的各个量子位的态来完成 ,每个量子位的态的测量 都是对各自的基本态进行的 . 以 2位量子寄存器为 例 ,其叠加态|j〉为 |j〉= T00|00〉+ T01|01〉 + T10|10〉 + T11|11〉.

​ 当多个量子位处于纠缠态时 ,对部分量子位的 态的测量将影响其它量子位的态的测量. 例如测量 |j〉A 时 ,测量一个量子位的态 ,将使另一个量子位 的态与之相同;测量|j〉B 时 ,测量一个量子位的态 , 将使另一个量子位的态与之相反. 但测量|j〉C 时 ,对右边那位的态不管如何测量 ,左边那位的态总是 为|0〉.

量子逻辑门和量子逻辑网络

对量子位的态进行变换 ,可以实现某些逻辑功 能. 变换所起的作用相当于逻辑门所起的作用 ,在 一定的时间间隔内实现逻辑变换的量子装置称为量 子逻辑门. 量子逻辑网络由多个量子逻辑门组成 ,这些量子逻辑门的操作在时间上同步.

量子逻辑门的可逆性

为了维持量子位的态所在的 Hilbert空间的本 征态的正交归一性 ,对量子位的态进行变换的算符 Uf 应为幺正 ( unitary )矩阵 ,即

​ 为了保证量子逻辑门的可逆性 ,除了使量子位 的态进行变换的算符为幺正矩阵外 ,还应使量子逻 辑门的输入端数和输出端数相等. 如何使它们相等 呢? 可将部分输入或全部输入直接送到输出端 ,和 / 或在输入处增加若干个|0〉作为输入 ,使输出端数增 加到和输入端数相等 .

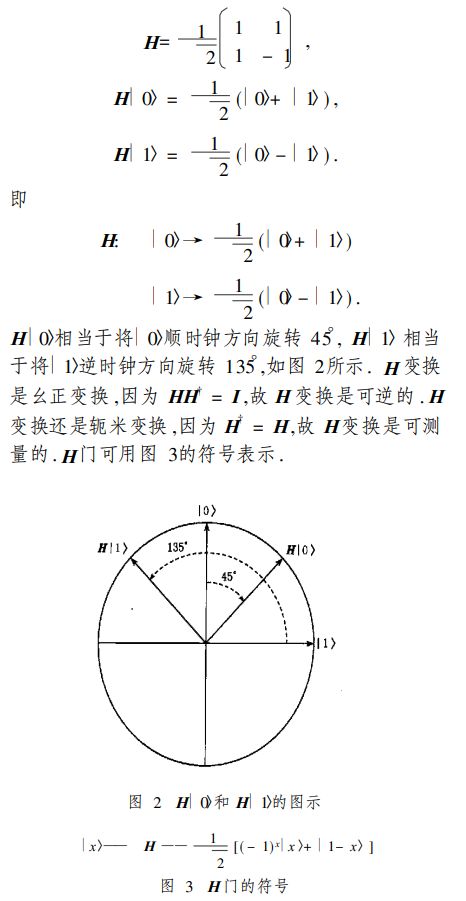
量子“非”门 ;H门

所以 ,对处于叠加态的|x〉进行 Uf 变换 ,可以产生 所有 x 的|f ( x )〉 . 量子计算机的这种特性称为量 子并行 ( quantum parallelism). 在常规计算机 中 ,计算所有 x 的 f (x )需要 2^n 次循环或 2^n 个处理 器并行工作 ,而在量子计算机中 ,只要一次变换就可 完成.

量子计算机的组织结构

量子计算机的计算过程由算法决定 ,不同的算 法有不同的幺正变换.计算过程如图 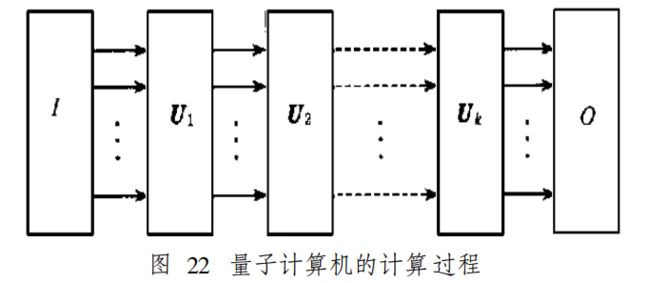所示 ,图中 的 I将输入数据置于所需的初始态 ,Ui (i= 1, 2,… , k )为幺正变换 ,输入数据的态经过 U1 ,U2 ,… ,Uk 后 , 由 O测量得出结果 . 量子计算机的计算过程可由常 规计算机控制 ,图是一个简单量子计算机的控制示意图.由于量子计算的测量结果是概率性的 ,需要 计算和测量多次 ,才能得到所需结果.

​ 量子并行是量子计算机的特点 ,对于串行计算及迭代运算,量子计算机不具备优势.量子计算机适合于作为常规的通用计算机的高速协处理器或外围专用处理机 ,或专门为实现某种量子算法或模拟某种量子系统的专用计算机 .目前研究的量子计算机原则上都是连接在常规通用计算机上的专用处 理机 ,它的编程语言是在通用计算机的编程语言中增加一些量子计算的成分. 专用量子处理机和常规的通用计算机的接口 , 或专用量子计算机和常规输入输出设备的接口也需要解决.

​ 量子计算是量子力学的新进展 ,它是一种和传 统的计算方式迥然不同的新型计算 .其概念是全新 的 ,它将使计算技术进入一种前所未有的新境界 .对 于某些问题 ,量子计算机可以达到常规计算机不能 达到的解题速度.量子计算机可以解决常规计算机 不能解决的某些问题.目前 ,量子计算仅处于起步阶 段 ,如果以后能研制出有实用价值的量子计算机 ,就 可以使人类更好地探索自然和驾驭自然.