统计学习方法--朴素贝叶斯法
与公众号同步更新,详细内容及相关ipynb文件在公众号中,公众号:AI入门小白
补充:对于统计学习方法的第一章节的部分概念和数学公式已放置到公众号中,需要的朋友可直接去公众号中下载
文章目录
-
- 朴素贝叶斯法的学习与分类
-
- 基本方法
- 后验概率最大化的含义
- 朴素贝叶斯法的参数估计
-
- 极大似然估计
- 学习与分类算法
- 贝叶斯估计
- 代码部分
-
- 数据准备
- GaussianNB高斯朴素贝叶斯
- scikit-learn实例
- 第4章朴素贝叶斯法-习题
-
- 习题4.1
- 习题4.2
朴素贝叶斯(naïve Bayes) 法是基于贝叶斯定理与特征条件独立假设的分类方法。
朴素贝叶斯法与贝叶斯估计(Bayesian estimation) 是不同的概念。
对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布:然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。
事情还没有发生,要求这件事情发生的可能性的大小,是先验概率。事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率。
贝叶斯公式:
P ( B i ∣ A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( B j ) P ( A ∣ B j ) P(B_i \mid A) = \frac{P(B_i)P(A \mid B_i)}{\sum_{j=1}^{n} P(B_j)P(A \mid B_j)} P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)
公式中,事件 B i B_i Bi的概率为 P ( B i ) P(B_i) P(Bi),事件 B i B_i Bi已发生条件下事件 A A A的概率为 P ( A ∣ B i ) P(A \mid B_i) P(A∣Bi),事件 A A A发生条件下事件 B i B_i Bi的概率为 P ( B i ∣ A ) P(B_i \mid A) P(Bi∣A)
朴素贝叶斯法的学习与分类
基本方法
设输入空间 X ⊆ R n \mathcal{X} \subseteq R^n X⊆Rn为 n n n维向量的集合,输出空间为类标记集合 Y = { c 1 , c 2 , ⋯ , c K } \mathcal{Y} = \{ c_1, c_2, \cdots, c_K\} Y={c1,c2,⋯,cK}。输入为特征向量 x ∈ X x \in \mathcal{X} x∈X,输出为类标记(class label) y ∈ Y y \in \mathcal{Y} y∈Y。 X X X是定义在输入空间 X \mathcal{X} X上的随机向量, Y Y Y是定义在输出空间 Y \mathcal{Y} Y上的随机变量。 P ( X , Y ) P(X, Y) P(X,Y)是 X X X和 Y Y Y的联合概率分布。训练数据集:
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
由 P ( X , Y ) P(X, Y) P(X,Y)独立同分布产生。
朴素贝叶斯法通过训练数据集学习联合概率分布 P ( X , Y ) P(X, Y) P(X,Y)。具体地,学习以下先验概率分布及条件概率分布。先验概率分布
P ( Y = c k ) , k = 1 , 2 , ⋯ , K (4.1) P(Y = c_k), k = 1, 2, \cdots, K \tag{4.1} P(Y=ck),k=1,2,⋯,K(4.1)
条件概率分布
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , ⋯ , X ( n ) = x ( n ) ∣ Y = c k ) , k = 1 , 2 , ⋯ , K (4.2) P(X=x \mid Y=c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} \mid Y=c_k), k = 1,2,\cdots,K \tag{4.2} P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck),k=1,2,⋯,K(4.2)
于是学习到联合概率分布 P ( X , Y ) P(X, Y) P(X,Y)。
条件概率分布 P ( X = x ∣ Y = c k ) P(X=x \mid Y=c_k) P(X=x∣Y=ck)有指数级数量的参数,其估计实际是不可行的。事实上,假设 x ( j ) x^{(j)} x(j)可取值有 S j S_j Sj个, j = 1 , 2 , ⋯ , n j=1,2,\cdots,n j=1,2,⋯,n, Y Y Y可取值有 K K K个,那么参数个数为 K ∏ j = 1 n S j K\prod_{j=1}^n S_j K∏j=1nSj。
朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设,朴素贝叶斯法也由此得名。具体地,条件独立性假设是
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , ⋯ , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) (4.3) \begin{aligned} P(X=x \mid Y=c_k) &= P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} \mid Y=c_k) \\ &= \prod_{j=1}^n P(X^{(j)} = x^{(j)} \mid Y=c_k) \end{aligned} \tag{4.3} P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)(4.3)
朴素贝叶斯法实际上学习到生成数据的机制,所以属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
朴素贝叶斯法分类时,对给定的输入 x x x,通过学习到的模型计算后验概率分布 P ( Y = c k ∣ X = x ) P(Y=c_k \mid X=x) P(Y=ck∣X=x), 将后验概率最大的类作为 x x x的类输出。后验概率计算根据贝叶斯定理进行:
P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( X = x ∣ Y = c k ) P ( Y = c k ) (4.4) P(Y=c_k \mid X=x) = \frac{P(X=x \mid Y=c_k)P(Y = c_k)}{\sum_k P(X=x \mid Y=c_k)P(Y = c_k)} \tag{4.4} P(Y=ck∣X=x)=∑kP(X=x∣Y=ck)P(Y=ck)P(X=x∣Y=ck)P(Y=ck)(4.4)
将式(4.3) 代入式(4.4) ,有
P ( Y = c k ∣ X = x ) = P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) , k = 1 , 2 , ⋯ , K (4.5) P(Y=c_k \mid X=x) = \frac{P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} \mid Y=c_k)}{\sum_k P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} \mid Y=c_k)}, k = 1, 2, \cdots, K \tag{4.5} P(Y=ck∣X=x)=∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck),k=1,2,⋯,K(4.5)
这是朴素贝叶斯法分类的基本公式。于是, 朴素贝叶斯分类器可表示为
y = f ( x ) = a r g max c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) (4.6) y = f(x) = arg \max_{c_k} \frac{P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} \mid Y=c_k)}{\sum_k P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} \mid Y=c_k)} \tag{4.6} y=f(x)=argckmax∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)(4.6)
注意到,在式(4.6) 中分母对所有 c k c_k ck都是相同的,所以,
y = a r g max c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) (4.7) y = arg \max_{c_k} P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} \mid Y=c_k) \tag{4.7} y=argckmaxP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)(4.7)
后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中。这等价于期望风险最小化。假设选择0-1 损失函数:
L ( Y , f ( x ) ) = { 1 , Y ≠ f ( X ) 0 , Y = f ( X ) L(Y, f(x)) = \begin{cases} 1, Y \neq f(X) \\ 0, Y = f(X) \end{cases} L(Y,f(x))={1,Y=f(X)0,Y=f(X)
式中 f ( X ) f(X) f(X)是分类决策函数。这时,期望风险函数为
R e x p ( f ) = E [ L ( Y , f ( X ) ) ] R_{exp}(f) = E[L(Y, f(X))] Rexp(f)=E[L(Y,f(X))]
期望是对联合分布 P ( X , Y ) P(X, Y) P(X,Y)取的。由此取条件期望
R e x p ( f ) = E x ∑ k = 1 K [ L ( c k , f ( X ) ) ] P ( c k ∣ X ) R_{exp}(f) = E_x \sum_{k=1}^K [L(c_k, f(X))] P(c_k \mid X) Rexp(f)=Exk=1∑K[L(ck,f(X))]P(ck∣X)
为了使期望风险最小化,只需对 X = x X = x X=x逐个极小化,由此得到:
f ( x ) = a r g min y ∈ Y ∑ k = 1 K L ( c k , y ) P ( c k ∣ X = x ) = a r g min y ∈ Y ∑ k = 1 K P ( y ≠ c k ∣ X = x ) = a r g min y ∈ Y ( 1 − P ( y = c k ∣ X = x ) ) = a r g min y ∈ Y P ( y = c k ∣ X = x ) \begin{aligned} f(x) &= arg \min_{y \in \mathcal{Y}} \sum_{k=1}^K L(c_k, y) P(c_k \mid X = x) \\ &= arg \min_{y \in \mathcal{Y}} \sum_{k=1}^K P(y \neq c_k \mid X = x) \\ &= arg \min_{y \in \mathcal{Y}} (1 - P(y = c_k \mid X = x)) \\ &= arg \min_{y \in \mathcal{Y}} P(y = c_k \mid X = x) \end{aligned} f(x)=argy∈Ymink=1∑KL(ck,y)P(ck∣X=x)=argy∈Ymink=1∑KP(y=ck∣X=x)=argy∈Ymin(1−P(y=ck∣X=x))=argy∈YminP(y=ck∣X=x)
这样一来,根据期望风险最小化准则就得到了后验概率最大化准则:
f ( x ) = a r g max c k P ( c k ∣ X = x ) f(x) = arg \max_{c_k} P(c_k \mid X = x) f(x)=argckmaxP(ck∣X=x)
即朴素贝叶斯法所采用的原理。
相关理解:https://blog.csdn.net/rea_utopia/article/details/78881415
朴素贝叶斯法的参数估计
极大似然估计
在朴素贝叶斯法中,学习意味着估计 P ( Y = c k ) P(Y = c_k) P(Y=ck)和 P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)} = x^{(j)} \mid Y = c_k) P(X(j)=x(j)∣Y=ck)。可以应用极大似然估计法估计相应的概率。先验概率 P ( Y = c k ) P(Y = c_k) P(Y=ck)的极大似然估计是
P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N , k = 1 , 2 , ⋯ , K (4.8) P(Y = c_k) = \frac{\sum_{i=1}^N I(y_i = c_k)}{N}, k = 1, 2, \cdots, K \tag{4.8} P(Y=ck)=N∑i=1NI(yi=ck),k=1,2,⋯,K(4.8)
设第 j j j个特征 x ( j ) x^{(j)} x(j)可能取值的集合为 a j 1 , a j 2 , ⋯ , a j s j {a_{j1}, a_{j2}, \cdots, a_j s_j} aj1,aj2,⋯,ajsj,条件概率 P ( X ( j ) = a j l ∣ Y = c k ) P(X^{(j)} = a_{jl} \mid Y = c_k) P(X(j)=ajl∣Y=ck)的极大似然估计是
P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) j = 1 , 2 , ⋯ , n ; l = 1 , 2 , ⋯ , S j ; k = 1 , 2 , ⋯ , K (4.9) P(X^{(j)} = a_{jl} \mid Y = c_k) = \frac{\sum_{i=1}^N I(x_i^{(j)} = a_{jl}, y_i = c_k)}{\sum_{i=1}^{N} I(y_i = c_k)} \\ j = 1, 2, \cdots, n; l = 1, 2, \cdots, S_j; k = 1, 2, \cdots, K \tag{4.9} P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)j=1,2,⋯,n;l=1,2,⋯,Sj;k=1,2,⋯,K(4.9)
式中, x i ( j ) x_i^{(j)} xi(j)是第 i i i个样本的第 j j j个特征; a i l a_{il} ail是第 j j j个特征可能取的第 l l l个值; I I I为指示函数。
I I I指示函数:当 y i = c k y_i = c_k yi=ck时 I ( y i = c k ) = 1 I(y_i = c_k) = 1 I(yi=ck)=1(不想等时为0),然后求和统计个数 ∑ i = 1 N I ( y i = c k ) \sum_{i=1}^N I(y_i = c_k) ∑i=1NI(yi=ck)
学习与分类算法
算法4. 1 ( 朴素贝叶斯算法( naïve Bayes algorithm) )
输入:训练数据 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中 x i = ( x i ( 1 ) , x i ( 2 ) , ⋯ , x i ( n ) ) T , x i ( j ) x_i=(x_i^{(1)}, x_i^{(2)}, \cdots, x_i^{(n)})^T, x_i^{(j)} xi=(xi(1),xi(2),⋯,xi(n))T,xi(j)是 i i i个样本的第 j j j个特征, x i ( j ) ∈ { a j 1 , a j 2 , ⋯ , a j S j } , a j l x_i^{(j)} \in \{a_{j1}, a_{j2}, \cdots, a_{jS_j}\}, a_{jl} xi(j)∈{aj1,aj2,⋯,ajSj},ajl是第 j j j个特征可能取的第 l l l个值, j = 1 , 2 , ⋯ , n , l = 1 , 2 , ⋯ , S j , y i ∈ { c 1 , c 2 , ⋯ , c K } j=1,2,\cdots,n, l=1,2,\cdots,S_j, y_i \in \{c_1, c_2, \cdots, c_K\} j=1,2,⋯,n,l=1,2,⋯,Sj,yi∈{c1,c2,⋯,cK};实例 x x x;
输出:实例 x x x的分类。
(1)计算先验概率及条件概率
P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N , k = 1 , 2 , ⋯ , K P(Y=c_k)=\frac{\sum_{i=1}^{N} I(y_i=c_k)}{N}, k=1, 2, \cdots, K P(Y=ck)=N∑i=1NI(yi=ck),k=1,2,⋯,K
P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)} P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)
j = 1 , 2 , ⋯ , n ; l = 1 , 2 , ⋯ , S j ; k = 1 , 2 , ⋯ , K j=1,2,\cdots,n; l=1,2,\cdots,S_j; k=1,2,\cdots,K j=1,2,⋯,n;l=1,2,⋯,Sj;k=1,2,⋯,K
(2)对于给定的实例 x = ( x ( 1 ) , x ( 2 ) , ⋯ , x ( n ) ) T x=(x^{(1)},x^{(2)},\cdots,x^{(n)})^T x=(x(1),x(2),⋯,x(n))T,计算
P ( Y = c k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) , k = 1 , 2 , ⋯ , K P(Y=c_k)\prod_{j=1}^{n} P(X^{(j)} = x^{(j)}| Y=c_k), k=1,2,\cdots,K P(Y=ck)j=1∏nP(X(j)=x(j)∣Y=ck),k=1,2,⋯,K
(3)确定实例 x x x的类
y = a r g max c k P ( Y = c k ) ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) y=arg \max_{c_k} P(Y=c_k)\prod_{j=1}^{n} P(X^{(j)}=x^{(j)}|Y=c_k) y=argckmaxP(Y=ck)j=1∏nP(X(j)=x(j)∣Y=ck)
例4.1 试由表4.1的训练数据学习一个朴素贝叶斯分类器并确定 x = ( 2 , S ) T x=(2, S)^T x=(2,S)T的类标记 y y y。表中 X ( 1 ) , X ( 2 ) X^{(1)}, X^{(2)} X(1),X(2)为特征,取值的集合分别为 A 1 = { 1 , 2 , 3 } , A 2 = { S , M , L } , Y A_1=\{1,2,3\},A_2=\{S,M,L\},Y A1={1,2,3},A2={S,M,L},Y为类标记, Y ∈ C = { 1 , − 1 } Y \in C =\{1, -1\} Y∈C={1,−1}

解 根据算法4.1,由表4.1,容易计算下列概率:
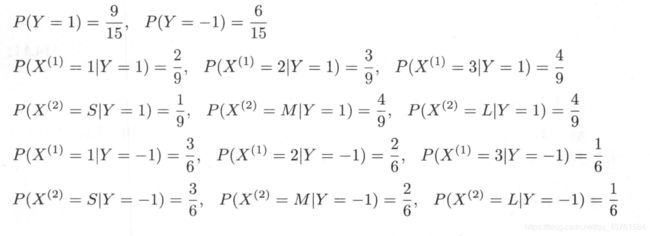
对于给定的 x = ( 2 , S ) T x=(2,S)^T x=(2,S)T计算:

因为 P ( Y = − 1 ) P ( X ( 1 ) = 2 ∣ Y = − 1 ) P ( X ( 2 ) = S ∣ Y = − 1 ) P(Y=-1)P(X^{(1)}=2 | Y=-1)P(X^{(2)}=S | Y=-1) P(Y=−1)P(X(1)=2∣Y=−1)P(X(2)=S∣Y=−1)最大,所以 y = − 1 y=-1 y=−1。
贝叶斯估计
用极大似然估计可能会出现所要估计的概率值为0 的情况。这时会影响到后验概率的计算结果,使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。具体地,条件概率的贝叶斯估计是

式中 λ ≥ 0 \lambda \geq 0 λ≥0。等价于在随机变量各个取值的频数上赋予一个正数 λ ≥ 0 \lambda \geq 0 λ≥0。当 λ = 0 \lambda = 0 λ=0时就是极大似然估计。常取 λ = 1 \lambda = 1 λ=1,这时称为拉普拉斯平滑(Laplacian smoothing) 。显然,对任何 l = 1 , 2 , ⋯ , S j , k = 1 , 2 , ⋯ , K l=1,2,\cdots,S_j, k=1,2,\cdots,K l=1,2,⋯,Sj,k=1,2,⋯,K,有
P λ ( X ( j ) = a j l ∣ Y = c k ) > 0 P_{\lambda} (X^{(j)}=a_{jl} | Y=c_k) > 0 Pλ(X(j)=ajl∣Y=ck)>0
∑ l = 1 S j P ( X ( j ) = a j l ∣ Y = c k ) = 1 \sum_{l=1}^{S_j} P(X^{(j)}=a_{jl} | Y=c_k) = 1 l=1∑SjP(X(j)=ajl∣Y=ck)=1
表明式(4.10) 确为一种概率分布。同样,先验概率的贝叶斯估计是

例4.2 问题同例4.1,按照拉普拉斯平滑估计概率,即取 λ = 1 \lambda=1 λ=1。
解 A 1 = 1 , 2 , 3 , A 2 = S , M , L , C = 1 , − 1 A_1={1,2,3}, A_2={S,M,L}, C={1,-1} A1=1,2,3,A2=S,M,L,C=1,−1。按照式(4.10) 和式(4.11) 计算下列概率:
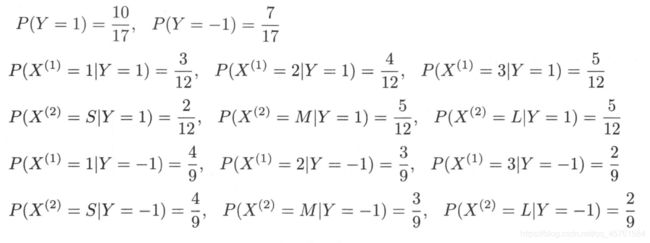
对于给定的 x = ( 2 , S ) T x=(2,S)^T x=(2,S)T,计算:

由于 P ( Y = − 1 ) P ( X ( 1 ) = 2 ∣ Y = − 1 ) P ( X ( 2 ) = S ∣ Y = − 1 ) P(Y=-1)P(X^{(1)}=2 | Y=-1)P(X^{(2)}=S | Y=-1) P(Y=−1)P(X(1)=2∣Y=−1)P(X(2)=S∣Y=−1)最大,所以 y = − 1 y=-1 y=−1。
代码部分
参考:https://machinelearningmastery.com/naive-bayes-classifier-scratch-python/
数据准备
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, :])
print(data[:6])
return data[:, :-1], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
X_test[0], y_test[0]
- 高斯模型
- 多项式模型
- 伯努利模型
GaussianNB高斯朴素贝叶斯
特征的可能性被假设为高斯概率密度函数(正态分布):
P ( x i ∣ y k ) = 1 2 π σ y k 2 e x p ( − ( x i − μ y k ) 2 2 σ y k 2 ) P(x_i | y_k)=\frac{1}{\sqrt{2\pi\sigma^2_{yk}}}exp(-\frac{(x_i-\mu_{yk})^2}{2\sigma^2_{yk}}) P(xi∣yk)=2πσyk21exp(−2σyk2(xi−μyk)2)
数学期望(mean): μ \mu μ
方差: σ 2 = ∑ ( X − μ ) 2 N \sigma^2=\frac{\sum(X-\mu)^2}{N} σ2=N∑(X−μ)2
class NaiveBayes:
def __init__(self):
self.model = None
# 数学期望;正态分布的期望、均数、中位数、众数相同,均等于μ
@staticmethod # @staticmethod: https://blog.csdn.net/polyhedronx/article/details/81911548
def mean(X):
return sum(X) / float(len(X))
# 标准差(均方差)
def stdev(self, X):
avg = self.mean(X)
return math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
# 概率密度函数
def gaussian_probability(self, x, mean, stdev):
exponent = math.exp(-(math.pow(x - mean, 2) /
(2 * math.pow(stdev, 2))))
return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent
# 处理X_train
def summarize(self, train_data):
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
return summaries
# 分类别求出数学期望和标准差
def fit(self, X, y):
labels = list(set(y))
data = {label: [] for label in labels}
for f, label in zip(X, y):
data[label].append(f) # data={(y:x),...}
self.model = {
label: self .summarize(value) # label: self .summarize(value)={(y:期望,标准差),...}
for label, value in data.items()
}
return 'gaussianNB train done!'
# 计算概率
def calculate_probabilities(self, input_data):
# summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
# input_data:[1.1, 2.2]
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1 # {(y1:1),(y2:1)...}
for i in range(len(value)):
mean, stdev = value[i]
# x_test使用训练集的期望和标准差,计算其在相对于的y中的概率
probabilities[label] *= self.gaussian_probability( # {(y1:概率),(y2:概率)...}
input_data[i], mean, stdev)
return probabilities
# 类别
def predict(self, X_test):
# {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
label = sorted(
self.calculate_probabilities(X_test).items(),
key=lambda x: x[-1]) [-1][0] # 找出概率最大时相对应的y
return label
# 计算分类正确的数量的比例
def score(self, X_test, y_test):
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y: # 若概率最大时相对应的y,与测试集中的y相等
right += 1
return right / float(len(X_test))
model = NaiveBayes()
model.fit(X_train, y_train)
![]()
print(model.predict([4.4, 3.2, 1.3, 0.2]))
![]()
model.score(X_test, y_test)
scikit-learn实例
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
clf.predict([[4.4, 3.2, 1.3, 0.2]])
![]()
from sklearn.naive_bayes import BernoulliNB, MultinomialNB # 伯努利模型和多项式模型
第4章朴素贝叶斯法-习题
习题4.1
用极大似然估计法推出朴素贝叶斯法中的概率估计公式(4.8)及公式 (4.9)。
解答:
第1步: 证明公式(4.8): P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N \displaystyle P(Y=c_k) = \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k)}{N} P(Y=ck)=Ni=1∑NI(yi=ck)
由于朴素贝叶斯法假设 Y Y Y是定义在输出空间 Y \mathcal{Y} Y上的随机变量,因此可以定义 P ( Y = c k ) P(Y=c_k) P(Y=ck)概率为 p p p。
令 m = ∑ i = 1 N I ( y i = c k ) \displaystyle m=\sum_{i=1}^NI(y_i=c_k) m=i=1∑NI(yi=ck),得出似然函数: L ( p ) = f D ( y 1 , y 2 , ⋯ , y n ∣ θ ) = ( N m ) p m ( 1 − p ) ( N − m ) L(p)=f_D(y_1,y_2,\cdots,y_n|\theta)=\binom{N}{m}p^m(1-p)^{(N-m)} L(p)=fD(y1,y2,⋯,yn∣θ)=(mN)pm(1−p)(N−m)使用微分求极值,两边同时对 p p p求微分: 0 = ( N m ) [ m p ( m − 1 ) ( 1 − p ) ( N − m ) − ( N − m ) p m ( 1 − p ) ( N − m − 1 ) ] = ( N m ) [ p ( m − 1 ) ( 1 − p ) ( N − m − 1 ) ( m − N p ) ] \begin{aligned} 0 &= \binom{N}{m}\left[mp^{(m-1)}(1-p)^{(N-m)}-(N-m)p^m(1-p)^{(N-m-1)}\right] \\ & = \binom{N}{m}\left[p^{(m-1)}(1-p)^{(N-m-1)}(m-Np)\right] \end{aligned} 0=(mN)[mp(m−1)(1−p)(N−m)−(N−m)pm(1−p)(N−m−1)]=(mN)[p(m−1)(1−p)(N−m−1)(m−Np)]可求解得到 p = 0 , p = 1 , p = m N \displaystyle p=0,p=1,p=\frac{m}{N} p=0,p=1,p=Nm
显然 P ( Y = c k ) = p = m N = ∑ i = 1 N I ( y i = c k ) N \displaystyle P(Y=c_k)=p=\frac{m}{N}=\frac{\displaystyle \sum_{i=1}^N I(y_i=c_k)}{N} P(Y=ck)=p=Nm=Ni=1∑NI(yi=ck),公式(4.8)得证。
第2步: 证明公式(4.9): P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) \displaystyle P(X^{(j)}=a_{jl}|Y=c_k) = \frac{\displaystyle \sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k)}{\displaystyle \sum_{i=1}^N I(y_i=c_k)} P(X(j)=ajl∣Y=ck)=i=1∑NI(yi=ck)i=1∑NI(xi(j)=ajl,yi=ck)
令 P ( X ( j ) = a j l ∣ Y = c k ) = p P(X^{(j)}=a_{jl}|Y=c_k)=p P(X(j)=ajl∣Y=ck)=p,令 m = ∑ i = 1 N I ( y i = c k ) , q = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) \displaystyle m=\sum_{i=1}^N I(y_i=c_k), q=\sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k) m=i=1∑NI(yi=ck),q=i=1∑NI(xi(j)=ajl,yi=ck),得出似然函数: L ( p ) = ( m q ) p q ( i − p ) m − q L(p)=\binom{m}{q}p^q(i-p)^{m-q} L(p)=(qm)pq(i−p)m−q使用微分求极值,两边同时对 p p p求微分: 0 = ( m q ) [ q p ( q − 1 ) ( 1 − p ) ( m − q ) − ( m − q ) p q ( 1 − p ) ( m − q − 1 ) ] = ( m q ) [ p ( q − 1 ) ( 1 − p ) ( m − q − 1 ) ( q − m p ) ] \begin{aligned} 0 &= \binom{m}{q}\left[qp^{(q-1)}(1-p)^{(m-q)}-(m-q)p^q(1-p)^{(m-q-1)}\right] \\ & = \binom{m}{q}\left[p^{(q-1)}(1-p)^{(m-q-1)}(q-mp)\right] \end{aligned} 0=(qm)[qp(q−1)(1−p)(m−q)−(m−q)pq(1−p)(m−q−1)]=(qm)[p(q−1)(1−p)(m−q−1)(q−mp)]可求解得到 p = 0 , p = 1 , p = q m \displaystyle p=0,p=1,p=\frac{q}{m} p=0,p=1,p=mq
显然 P ( X ( j ) = a j l ∣ Y = c k ) = p = q m = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) \displaystyle P(X^{(j)}=a_{jl}|Y=c_k)=p=\frac{q}{m}=\frac{\displaystyle \sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k)}{\displaystyle \sum_{i=1}^N I(y_i=c_k)} P(X(j)=ajl∣Y=ck)=p=mq=i=1∑NI(yi=ck)i=1∑NI(xi(j)=ajl,yi=ck),公式(4.9)得证。
习题4.2
用贝叶斯估计法推出朴素贝叶斯法中的慨率估计公式(4.10)及公式(4.11)
解答:
第1步: 证明公式(4.11): P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ \displaystyle P(Y=c_k) = \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k) + \lambda}{N+K \lambda} P(Y=ck)=N+Kλi=1∑NI(yi=ck)+λ
加入先验概率,在没有任何信息的情况下,可以假设先验概率为均匀概率(即每个事件的概率是相同的)。
可得 p = 1 K ⇔ p K − 1 = 0 ( 1 ) \displaystyle p=\frac{1}{K} \Leftrightarrow pK-1=0\quad(1) p=K1⇔pK−1=0(1)
根据习题4.1得出先验概率的极大似然估计是 p N − ∑ i = 1 N I ( y i = c k ) = 0 ( 2 ) \displaystyle pN - \sum_{i=1}^N I(y_i=c_k) = 0\quad(2) pN−i=1∑NI(yi=ck)=0(2)
存在参数 λ \lambda λ使得 ( 1 ) ⋅ λ + ( 2 ) = 0 (1) \cdot \lambda + (2) = 0 (1)⋅λ+(2)=0
所以有 λ ( p K − 1 ) + p N − ∑ i = 1 N I ( y i = c k ) = 0 \lambda(pK-1) + pN - \sum_{i=1}^N I(y_i=c_k) = 0 λ(pK−1)+pN−i=1∑NI(yi=ck)=0可得 P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ \displaystyle P(Y=c_k) = \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k) + \lambda}{N+K \lambda} P(Y=ck)=N+Kλi=1∑NI(yi=ck)+λ,公式(4.11)得证。
第2步: 证明公式(4.10): P λ ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ \displaystyle P_{\lambda}(X^{(j)}=a_{jl} | Y = c_k) = \frac{\displaystyle \sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k) + \lambda}{\displaystyle \sum_{i=1}^N I(y_i=c_k) + S_j \lambda} Pλ(X(j)=ajl∣Y=ck)=i=1∑NI(yi=ck)+Sjλi=1∑NI(xi(j)=ajl,yi=ck)+λ
根据第1步,可同理得到 P ( Y = c k , x ( j ) = a j l ) = ∑ i = 1 N I ( y i = c k , x i ( j ) = a j l ) + λ N + K S j λ P(Y=c_k, x^{(j)}=a_{j l})=\frac{\displaystyle \sum_{i=1}^N I(y_i=c_k, x_i^{(j)}=a_{jl})+\lambda}{N+K S_j \lambda} P(Y=ck,x(j)=ajl)=N+KSjλi=1∑NI(yi=ck,xi(j)=ajl)+λ
P ( x ( j ) = a j l ∣ Y = c k ) = P ( Y = c k , x ( j ) = a j l ) P ( y i = c k ) = ∑ i = 1 N I ( y i = c k , x i ( j ) = a j l ) + λ N + K S j λ ∑ i = 1 N I ( y i = c k ) + λ N + K λ = ( λ 可 以 任 意 取 值 , 于 是 取 λ = S j λ ) = ∑ i = 1 N I ( y i = c k , x i ( j ) = a j l ) + λ N + K S j λ ∑ i = 1 N I ( y i = c k ) + λ N + K S j λ = ∑ i = 1 N I ( y i = c k , x i ( j ) = a j l ) + λ ∑ i = 1 N I ( y i = c k ) + λ ( 其 中 λ = S j λ ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ \begin{aligned} P(x^{(j)}=a_{jl} | Y=c_k) &= \frac{P(Y=c_k, x^{(j)}=a_{j l})}{P(y_i=c_k)} \\ &= \frac{\displaystyle \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k, x_i^{(j)}=a_{jl})+\lambda}{N+K S_j \lambda}}{\displaystyle \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k) + \lambda}{N+K \lambda}} \\ &= (\lambda可以任意取值,于是取\lambda = S_j \lambda) \\ &= \frac{\displaystyle \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k, x_i^{(j)}=a_{jl})+\lambda}{N+K S_j \lambda}}{\displaystyle \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k) + \lambda}{N+K S_j \lambda}} \\ &= \frac{\displaystyle \sum_{i=1}^N I(y_i=c_k, x_i^{(j)}=a_{jl})+\lambda}{\displaystyle \sum_{i=1}^N I(y_i=c_k) + \lambda} (其中\lambda = S_j \lambda)\\ &= \frac{\displaystyle \sum_{i=1}^N I(x_i^{(j)}=a_{jl},y_i=c_k) + \lambda}{\displaystyle \sum_{i=1}^N I(y_i=c_k) + S_j \lambda} \end{aligned} P(x(j)=ajl∣Y=ck)=P(yi=ck)P(Y=ck,x(j)=ajl)=N+Kλi=1∑NI(yi=ck)+λN+KSjλi=1∑NI(yi=ck,xi(j)=ajl)+λ=(λ可以任意取值,于是取λ=Sjλ)=N+KSjλi=1∑NI(yi=ck)+λN+KSjλi=1∑NI(yi=ck,xi(j)=ajl)+λ=i=1∑NI(yi=ck)+λi=1∑NI(yi=ck,xi(j)=ajl)+λ(其中λ=Sjλ)=i=1∑NI(yi=ck)+Sjλi=1∑NI(xi(j)=ajl,yi=ck)+λ
公式(4.11)得证。
数据来源:统计学习方法(第二版) &
https://github.com/fengdu78/lihang-code
