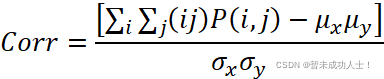机器学习图像特征提取—灰度共生矩阵(GLCM)纹理特征提取原理及代码实现
目录
1 灰度共生矩阵原理
2 灰度共生矩阵特征量
2.1 对比度
2.2 能量
2.3 熵
2.4 逆方差
2.5 相关性
3 灰度共生矩阵特征量提取代码
1 灰度共生矩阵原理
灰度共生矩阵,指的是一种通过研究灰度的空间相关特性来描述纹理的常用方法。1973年Haralick等人提出了用灰度共生矩阵来描述纹理特征。
由于纹理是由灰度分布在空间位置上反复出现而形成的,因而在图像空间中相隔某距离的两像素之间会存在一定的灰度关系,即图像中灰度的空间相关特性。
灰度共生矩阵被定义为从灰度为 i 的像素点出发,离开某个固定位置(相隔距离为d,方位为0°/45°/90°/135°)的点上灰度值为的概率,即,所有估计的值可以表示成一个矩阵的形式,以此被称为灰度共生矩阵。对于纹理变化缓慢的图像,其灰度共生矩阵对角线上的数值较大;而对于纹理变化较快的图像,其灰度共生矩阵对角线上的数值较小,对角线两侧的值较大。由于灰度共生矩阵的数据量较大,一般不直接作为区分纹理的特征,而是基于它构建的一些统计量作为纹理分类特征。Haralick曾提出了14种基于灰度共生矩阵计算出来的统计量:即:能量、熵、对比度、均匀性、相关性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。下图显示了如何求解灰度共生矩阵。看概念也是有点难理解,具体过程也可看B站视频讲解(影像组学之radiomics 提取特征的意义(2)_哔哩哔哩_bilibili)
2 灰度共生矩阵特征量
2.1 对比度
度量 矩阵的值是如何分布和图像中局部变化的多少,反应了图像的清晰度和纹理的沟纹深浅。纹理的沟纹越深,反差越大,效果越清晰;反之,对比值小,则沟纹浅,效果模糊。
2.2 能量
能量变换反映了图像灰度分布均匀程度和纹理粗细度。若灰度共生矩阵的元素值相近,则能量较小,表示纹理细致;若其中一些值大,而其它值小,则能量值较大。能量值大表明一种较均一和规则变化的纹理模式。
2.3 熵
图像包含信息量的随机性度量。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时,熵最大;因此熵值表明了图像灰度分布的复杂程度,熵值越大,图像越复杂。
2.4 逆方差
逆方差反映了图像纹理局部变化的大小,若图像纹理的不同区域间较均匀,变化缓慢,逆方差会较大,反之较小。
2.5 相关性
用来度量图像的灰度级在行或列方向上的相似程度,因此值得大小反应了局部灰度相关性,值越大,相关性也越大。
3 灰度共生矩阵特征量提取代码
以下代码提取了灰度共生矩阵的7个特征量:
# =============灰度共生矩阵========================
'''
灰度共生矩阵是像素距离和角度的矩阵函数,
它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,
来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
'''
import numpy as np
import cv2
import math
from matplotlib import pyplot as plt
#定义最大灰度级数
gray_level = 16
def maxGrayLevel(img):
max_gray_level=0
(height,width)=img.shape
print ("图像的高宽分别为:height,width",height,width)
for y in range(height):
for x in range(width):
if img[y][x] > max_gray_level:
max_gray_level = img[y][x]
print("max_gray_level:",max_gray_level)
return max_gray_level+1
def getGlcm(input,d_x,d_y):
srcdata=input.copy()
ret=[[0.0 for i in range(gray_level)] for j in range(gray_level)]
(height,width) = input.shape
max_gray_level=maxGrayLevel(input)
#若灰度级数大于gray_level,则将图像的灰度级缩小至gray_level,减小灰度共生矩阵的大小
if max_gray_level > gray_level:
for j in range(height):
for i in range(width):
srcdata[j][i] = srcdata[j][i]*gray_level / max_gray_level
if d_x >= 0 or d_y >= 0:
for j in range(height-d_y):
for i in range(width-d_x):
rows = srcdata[j][i]
cols = srcdata[j + d_y][i+d_x]
ret[rows][cols]+=1.0
else:
for j in range(height):
for i in range(width):
rows = srcdata[j][i]
cols = srcdata[j + d_y][i + d_x]
ret[rows][cols] += 1.0
for i in range(gray_level):
for j in range(gray_level):
ret[i][j]/=float(height*width)
return ret
def feature_computer(p):
#mean:均值
#con:对比度反应了图像的清晰度和纹理的沟纹深浅。纹理越清晰反差越大对比度也就越大。
#eng:熵(Entropy, ENT)度量了图像包含信息量的随机性,表现了图像的复杂程度。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时,熵最大。
#agm:角二阶矩(能量),图像灰度分布均匀程度和纹理粗细的度量。当图像纹理均一规则时,能量值较大;反之灰度共生矩阵的元素值相近,能量值较小。
#idm:反差分矩阵又称逆方差,反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大。
#Auto_correlation:相关性
mean=0.0
Con=0.0
Eng=0.0
Asm=0.0
Idm=0.0
Auto_correlation=0.0
std2=0.0
std=0.0
for i in range(gray_level):
for j in range(gray_level):
mean+=p[i][j]*i/gray_level**2
Con+=(i-j)*(i-j)*p[i][j]
Asm+=p[i][j]*p[i][j]
Idm+=p[i][j]/(1+(i-j)*(i-j))
Auto_correlation+=p[i][j]*i*j
if p[i][j]>0.0:
Eng+=p[i][j]*math.log(p[i][j])
for i in range(gray_level):
for j in range(gray_level):
std2+=(p[i][j]*i-mean)**2
std=np.sqrt(std2)
return mean,Asm,Con,-Eng,Idm,Auto_correlation,std
def test(image_name):
img = cv2.imread(image_name)
try:
img_shape=img.shape
except:
print ('imread error')
return
#这里如果用‘/’会报错TypeError: integer argument expected, got float
#其实主要的错误是因为 因为cv2.resize内的参数是要求为整数
img=cv2.resize(img,(img_shape[1]//2,img_shape[0]//2),interpolation=cv2.INTER_CUBIC)
#img = cv2.resize(img, dsize=(1000, 1000))
print(img.shape)
img_gray=cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
glcm_0=getGlcm(img_gray, 1,0)
#glcm_1=getGlcm(img_gray, 0,1)
#glcm_2=getGlcm(src_gray, 1,1)
#glcm_3=getGlcm(src_gray, -1,1)
#print(glcm_0)
plt.imshow(glcm_0)
plt.show()
mean,asm,con,eng,idm,Auto_correlation,std=feature_computer(glcm_0)
return [mean,asm,con,eng,idm,Auto_correlation,std]
if __name__=='__main__':
result1_3=test("./photo/2-5-1250.bmp")
参考来源:影像组学之radiomics 提取特征的意义(2)_哔哩哔哩_bilibili
灰度共生矩阵(超简单理解)_hello~bye~的博客-CSDN博客_灰度共生矩阵
灰度共生矩阵(附python代码)_hello~bye~的博客-CSDN博客_python 灰度共生矩阵