Temporal Graph Networks for Deep Learning on Dynamic Graphs
文章目录
-
- 1 前言
- 2 问题定义
- 3 TGN思路
-
- 3.1 Memory
- 3.2 Message Function
- 3.3 Message Aggregator
- 3.5 Memory Updater
- 3.5 Embeddings
- 4 方法的优势与局限性
- 论文地址:https://arxiv.org/pdf/2006.10637.pdf
- 来源:ICML 2020 Workshop
- slides:tgn
- 源码地址:tgn
- 关键词:graph representation, temporal graph
1 前言
该论文主要解决的是连续时间下的动态图的表示,论文中将连续时间下的动态图看成流图 — 由一系列的带时间戳的事件组成。
2 问题定义
论文中将动态图建模为带时间戳的事件序列: G = { x ( t 1 ) , x ( t 2 ) , … } \mathcal{G}=\left\{x\left(t_{1}\right), x\left(t_{2}\right), \ldots\right\} G={x(t1),x(t2),…}。事件 x ( t ) x(t) x(t)有两种类型:1)结点事件,新增一个结点或者更新一个结点的特征,用 v i ( t ) \mathbf{v}_i(t) vi(t)表示;2)交互事件:表示结点之间的交互,由 e i j ( t ) \mathbf{e}_{i j}(t) eij(t)表示。该论文的主要贡献就是建立了一个通用的框架来对动态图进行建模,并且将一系列的模块组合起来对动态图进行学习,得到结点在某个时间点上的表征。将TGN作用在一个连续时间的动态图上,将为每个结点在每个时间点上产生一个表征。
3 TGN思路
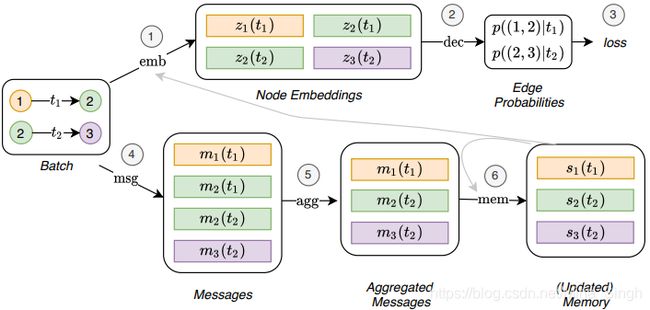
简言之,TGN可以看作一个编码器,共由5个子模块组成。
3.1 Memory
t t t时的模型的Memory由模型到 t t t时为止所见到的结点 i i i的状态 s i ( t ) \mathbf{s}_i(t) si(t)组成。结点的状态相当于对结点的历史信息的一个压缩形式的表示。
3.2 Message Function
t t t时,当有涉及 i i i结点的事件时,一条message会被计算用于更新 i i i的状态。论文中对两种事件的消息计算公式如下:
m i ( t ) = m s g s ( s i ( t − ) , s j ( t − ) , △ t , e i j ( t ) ) \mathbf{m}_i(t) = msg_s(\mathbf{s}_i(t^{-}), \mathbf{s}_j(t^{-}), \triangle t, \mathbf{e}_{ij}(t)) mi(t)=msgs(si(t−),sj(t−),△t,eij(t))
m j ( t ) = m s g d ( s j ( t − ) , s i ( t − ) , △ t , e i j ( t ) ) \mathbf{m}_j(t) = msg_d(\mathbf{s}_j(t^{-}), \mathbf{s}_i(t^{-}), \triangle t, \mathbf{e}_{ij}(t)) mj(t)=msgd(sj(t−),si(t−),△t,eij(t))
m i ( t ) = m s g n ( s i ( t − ) , t , v i ( t ) ) \mathbf{m}_i(t) = msg_n(\mathbf{s}_i(t^{-}), t, \mathbf{v}_{i}(t)) mi(t)=msgn(si(t−),t,vi(t))
m s g s , m s g t , m s g n msg_s, msg_t, msg_n msgs,msgt,msgn分别表示交互事件中源节点和目标节点、结点事件中所涉及的结点的消息的计算公式。具体实现时可以有多种形式,如MLP,在论文中采用的是拼接的形式。
3.3 Message Aggregator
由于在实际中通常会采用一次性处理多个事件(可能是多个时间的多个事件),需要将多个事件对应的message汇聚,形式如下:
m ˉ i ( t ) = a g g ( m i ( t 1 ) , . . . , m i ( t b ) ) \bar{\mathbf{m}}_i(t) = agg(\mathbf{m}_i(t_1), ..., \mathbf{m}_i(t_b)) mˉi(t)=agg(mi(t1),...,mi(tb))
a g g agg agg的具体实现形式也可以是多样的,如RNN、mean等,论文中采用的是只选择最近的message。
3.5 Memory Updater
得到了 t t t时设计到 i i i的message后就可以更新状态了。
s i ( t ) = m e m ( m ˉ i ( t ) , s i ( t − ) ) \mathbf{s}_i(t) = mem(\bar{m}_i(t), \mathbf{s}_i(t^-)) si(t)=mem(mˉi(t),si(t−))
同样, m e m mem mem的形式也可以是多样的,如LSTM、GRU等。
3.5 Embeddings
这个模块是用于为 i i i生成在 t t t时的表征的:
KaTeX parse error: Expected group after '\mathbf' at position 136: …}_i(t), \mathbf_̲{v}_j(t))
h h h的具体形式也是多样的。
4 方法的优势与局限性
- 对连续时间下的动态图进行了建模,以事件序列表示一个动态图
- 对动态图的表征学习提出了一个统一的框架
- 可应用于异常检测、金融交易等场景中
欢迎访问我的个人博客~~~