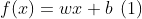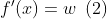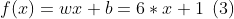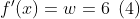华为AI计算框架昇思MindSpore零基础快速入门 (下)

六、自动微分

• 自动微分：求导 - 梯度缩放 - 停止计算
• 自动微分能够计算可导函数在某点处的导数值，是反向传播算法的一般化
• 自动微分主要解决的问题是将一个复杂的数学运算分解为一系列简单的基本运算，该功能对用户屏蔽了大量的求导细节和过程，大大降低了框架的使用门槛
• MindSpore使用ops.GradOperation计算一阶导数，ops.GradOperation属性如下
  • get_all：是否对输入参数进行求导，默认值为False
  • get_by_list：是否对权重参数进行求导，默认值为False
  • sens_param：是否对网络的输出值做缩放以改变最终梯度，默认值为False

1. 对输入求一阶导

• 对输入求导前需要先定义公式：
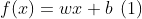
• 下面示例代码是上述公式的表达，由于MindSpore采用函数式编程，因此所有计算公式表达都采用函数进行表示

import numpy as np
import mindspore.nn as nn
from mindspore import Parameter, Tensor

class Net(nn.Cell):
    def __init__(self):
        super(Net, self).__init__()
        self.w = Parameter(np.array([6.0]), name='w')
        self.b = Parameter(np.array([1.0]), name='b')

    def construct(self, x):
        f = self.w * x + self.b
        return f

• 然后定义求导类GradNet，类的_init_函数中定义需要求导的网络，self.net和ops.GradOperation操作，类的construct函数中对self.net的输入进行求导，其对应MindSpore内部会产生公式：

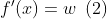
from mindspore import dtype as mstype
import mindspore.ops as ops

class GradNet(nn.Cell):
    def __init__(self, net):
        super(GradNet, self).__init__()
        self.net = net
        self.grad_op = ops.GradOperation()

    def construct(self, x):
        gradient_function = self.grad_op(self.net)
        return gradient_function(x)

• 最后定义权重参数为w，并对输入公式(1)中的输入参数x求一阶导数，从运行结果来看，公式(1)中的输入为6，即：
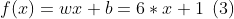
• 对上式进行求导，有：

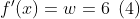
x = Tensor([100], dtype=mstype.float32)
output = GradNet(Net())(x)

print(output)  # [6.]

• MindSpore计算一阶导数方法ops.GradOperation(get_all=False, get_by_list=False, sens_param=False)，其中get_all为False时，只会对第一个输入求导，为True时，会对所有输入求导

2. 对权重求一阶导

• 对权重参数求一阶导，需要将ops.GradOperation中的get_by_list设置为True

from mindspore import ParameterTuple

class GradNet(nn.Cell):
    def __init__(self, net):
        super(GradNet, self).__init__()
        self.net = net
        self.params = ParameterTuple(net.trainable_params())
        self.grad_op = ops.GradOperation(get_by_list=True)  # 设置对权重参数进行一阶求导

    def construct(self, x):
        gradient_function = self.grad_op(self.net, self.params)
        return gradient_function(x)

• 接下来，对函数进行求导

# 对函数进行求导计算
x = Tensor([100], dtype=mstype.float32)
fx = GradNet(Net())(x)

# 打印结果
print(f"wgrad: {fx[0]}\nbgrad: {fx[1]}")
'''
wgrad: [100.]
bgrad: [1.]
'''

• 若某些权重不需要进行求导，则在定义求导网络时，相应的权重参数声明定义的时候，将其属性requires_grad需设置为False

class Net(nn.Cell):
    def __init__(self):
        super(Net, self).__init__()
        self.w = Parameter(Tensor(np.array([6], np.float32)), name='w')
        self.b = Parameter(Tensor(np.array([1.0], np.float32)), name='b', requires_grad=False)

    def construct(self, x):
        out = x * self.w + self.b
        return out

class GradNet(nn.Cell):
    def __init__(self, net):
        super(GradNet, self).__init__()
        self.net = net
        self.params = ParameterTuple(net.trainable_params())
        self.grad_op = ops.GradOperation(get_by_list=True)

    def construct(self, x):
        gradient_function = self.grad_op(self.net, self.params)
        return gradient_function(x)

# 构建求导网络
x = Tensor([5], dtype=mstype.float32)
fw = GradNet(Net())(x)

print(fw)  # (Tensor(shape=[1], dtype=Float32, value= [ 5.00000000e+00]),)

3. 梯度值缩放

• 通过sens_param参数对网络的输出值做缩放以改变最终梯度
• 首先将ops.GradOperation中的sens_param设置为True，并确定缩放指数，其维度与输出维度保持一致

class GradNet(nn.Cell):
    def __init__(self, net):
        super(GradNet, self).__init__()
        self.net = net
        # 求导操作
        self.grad_op = ops.GradOperation(sens_param=True)
        # 缩放指数
        self.grad_wrt_output = Tensor([0.1], dtype=mstype.float32)

    def construct(self, x):
        gradient_function = self.grad_op(self.net)
        return gradient_function(x, self.grad_wrt_output)

x = Tensor([6], dtype=mstype.float32)
output = GradNet(Net())(x)

print(output)  # [0.6]

4. 停止计算梯度

• 使用ops.stop_gradient可以停止计算梯度

from mindspore.ops import stop_gradient

class Net(nn.Cell):
    def __init__(self):
        super(Net, self).__init__()
        self.w = Parameter(Tensor(np.array([6], np.float32)), name='w')
        self.b = Parameter(Tensor(np.array([1.0], np.float32)), name='b')

    def construct(self, x):
        out = x * self.w + self.b
        # 停止梯度更新，out对梯度计算无贡献
        out = stop_gradient(out)
        return out

class GradNet(nn.Cell):
    def __init__(self, net):
        super(GradNet, self).__init__()
        self.net = net
        self.params = ParameterTuple(net.trainable_params())
        self.grad_op = ops.GradOperation(get_by_list=True)

    def construct(self, x):
        gradient_function = self.grad_op(self.net, self.params)
        return gradient_function(x)

x = Tensor([100], dtype=mstype.float32)
output = GradNet(Net())(x)

print(f"wgrad: {output[0]}\nbgrad: {output[1]}")
'''
wgrad: [0.]
bgrad: [0.]
'''

七、模型训练

• 模型训练：超参 - 损失函数 - 优化器 - 训练

1. 超参

• 超参是可以调整的参数，可以控制模型训练优化的过程，不同的超参数值可能会影响模型训练和收敛速度
• 目前深度学习模型多采用批量随机梯度下降算法进行优化，随机梯度下降算法的原理如下
  • 
• 式中，n是批量大小 (batch size)，η是学习率 (learning rate)，wt为训练轮次t中权重参数，∇l为损失函数的导数
• 除了梯度本身，这两个因子直接决定了模型的权重更新，从优化本身来看它们是影响模型性能收敛最重要的参数
• 一般会定义以下超参用于训练
  • 训练轮次 (epoch)：训练时遍历数据集的次数
  • 批次大小 (batch size)：数据集进行分批读取训练，设定每个批次数据的大小。batch size过小，花费时间多，同时梯度震荡严重，不利于收敛；batch size过大，不同batch的梯度方向没有任何变化，容易陷入局部极小值，因此需要选择合适的batch size，可以有效提高模型精度、全局收敛
  • 学习率 (learning rate)：如果学习率偏小，会导致收敛的速度变慢，如果学习率偏大则可能会导致训练不收敛等不可预测的结果，梯度下降法是一个广泛被用来最小化模型误差的参数优化算法，梯度下降法通过多次迭代，并在每一步中最小化损失函数来估计模型的参数，学习率就是在迭代过程中，会控制模型的学习进度

epochs = 10
batch_size = 32
momentum = 0.9
learning_rate = 1e-2

2. 损失函数

• 损失函数用来评价模型的预测值和目标值之间的误差，在这里，使用绝对误差损失函数L1Loss
  • 
• mindspore.nn.loss也提供了许多其他常用的损失函数，如、MSELoss、SmoothL1Loss、SoftmaxCrossEntropyWithLogits
• 我们给定预测值和目标值，通过损失函数计算预测值和目标值之间的误差

import numpy as np
import mindspore.nn as nn
from mindspore import Tensor

loss = nn.L1Loss()
output_data = Tensor(np.array([[1, 2, 3], [2, 3, 4]]).astype(np.float32))
target_data = Tensor(np.array([[0, 2, 5], [3, 1, 1]]).astype(np.float32))

print(loss(output_data, target_data))  # 1.5

3. 优化器函数

• 优化器函数用于计算和更新梯度，模型优化算法的选择直接关系到最终模型的性能
• 有时候最终模型效果不好，未必是特征或者模型设计的问题，很有可能是优化算法的问题
• MindSpore所有优化逻辑都封装在Optimizer对象中，在这里，我们使用Momentum优化器，mindspore.nn也提供了许多其他常用的优化器函数，如Adam、SGD、RMSProp
• 我们需要构建一个Optimizer对象，这个对象能够基于计算得到的梯度对参数进行更新，为了构建一个Optimizer，需要给它一个包含可优化的参数，如网络中所有可以训练的parameter，即设置优化器的入参为net.trainable_params()
• 然后设置Optimizer的参数选项，如学习率、权重衰减等

from mindspore import nn
from mindvision.classification.models import lenet

net = lenet(num_classes=10, pretrained=False)
optim = nn.Momentum(net.trainable_params(), learning_rate, momentum)

4. 模型训练

• 模型训练一般分为4个步骤
  • 构建数据集
  • 定义神经网络
  • 定义超参、损失函数及优化器
  • 输入训练轮次和数据集进行训练

import mindspore.nn as nn
from mindspore.train import Model

from mindvision.classification.dataset import Mnist
from mindvision.classification.models import lenet
from mindvision.engine.callback import LossMonitor

# 1. 构建数据集
download_train = Mnist(path="./mnist", split="train", batch_size=batch_size, repeat_num=1, shuffle=True, resize=32, download=True)
dataset_train = download_train.run()

# 2. 定义神经网络
network = lenet(num_classes=10, pretrained=False)
# 3.1 定义损失函数
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
# 3.2 定义优化器函数
net_opt = nn.Momentum(network.trainable_params(), learning_rate=learning_rate, momentum=momentum)
# 3.3 初始化模型参数
model = Model(network, loss_fn=net_loss, optimizer=net_opt, metrics={'acc'})

# 4. 对神经网络执行训练
model.train(epochs, dataset_train, callbacks=[LossMonitor(learning_rate, 1875)])

• 训练过程中会打印loss值，loss值会波动，但总体来说loss值会逐步减小，精度逐步提高。每个人运行的loss值有一定随机性，不一定完全相同

八、保存与加载

• 保存与加载：模型保存 - 加载模型 - 迁移学习

1. 模型训练

• 以MNIST数据集为例，介绍网络模型的保存与加载方式
• 首先，需要获取MNIST数据集并训练模型，随着训练轮次的增加，损失值趋于收敛

import mindspore.nn as nn
from mindspore.train import Model

from mindvision.classification.dataset import Mnist
from mindvision.classification.models import lenet
from mindvision.engine.callback import LossMonitor

epochs = 10  # 训练轮次

# 1. 构建数据集
download_train = Mnist(path="./mnist", split="train", batch_size=32, repeat_num=1, shuffle=True, resize=32, download=True)
dataset_train = download_train.run()

# 2. 定义神经网络
network = lenet(num_classes=10, pretrained=False)
# 3.1 定义损失函数
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
# 3.2 定义优化器函数
net_opt = nn.Momentum(network.trainable_params(), learning_rate=0.01, momentum=0.9)
# 3.3 初始化模型参数
model = Model(network, loss_fn=net_loss, optimizer=net_opt, metrics={'accuracy'})

# 4. 对神经网络执行训练
model.train(epochs, dataset_train, callbacks=[LossMonitor(0.01, 1875)])

2. 保存模型

• 在训练完网络完成后，将网络模型以文件的形式保存下来，保存模型的接口有主要2种
  • 简单的对网络模型进行保存，可以在训练前后进行保存，这种方式的优点是接口简单易用，但是只保留执行命令时候的网络模型状态
  • 在网络模型训练中进行保存，MindSpore在网络模型训练的过程中，自动保存训练时候设定好的epoch数和step数的参数，也就是把模型训练过程中产生的中间权重参数也保存下来，方便进行网络微调和停止训练
• 直接保存模型
  • 使用MindSpore提供的save_checkpoint保存模型，传入网络和保存路径
  • 其中，network为训练网络，"./MyNet.ckpt"为网络模型的保存路径

import mindspore as ms

# 定义的网络模型为net，一般在训练前或者训练后使用
ms.save_checkpoint(network, "./MyNet.ckpt")

• 训练过程中保存模型
  • 在模型训练的过程中，使用model.train里面的callbacks参数传入保存模型的对象ModelCheckpoint (一般与CheckpointConfig配合使用)，可以保存模型参数，生成CheckPoint (简称ckpt) 文件
  • 用户可以根据具体需求通过设置CheckpointConfig来对CheckPoint策略进行配置
  • 首先需要初始化一个CheckpointConfig类对象，用来设置保存策略
    • save_checkpoint_steps表示每隔多少个step保存一次，可以设置为训练数据集的总数除以每个batch_size的大小
    • keep_checkpoint_max表示最多保留CheckPoint文件的数量，一般设置得比较大
    • prefix表示生成CheckPoint文件的前缀名
    • directory表示存放文件的目录
  • 创建一个ModelCheckpoint对象把它传递给model.train方法，就可以在训练过程中使用CheckPoint功能了
  • 如果用户使用相同的前缀名，运行多次训练脚本，可能会生成同名CheckPoint文件
  • MindSpore为方便用户区分每次生成的文件，会在用户定义的前缀后添加”_”和数字加以区分，如果想要删除.ckpt文件时，请同步删除.meta文件
  • lenet_3-2_1875.ckpt表示运行第3次脚本生成的第2个epoch的第1875个step的CheckPoint文件

from mindspore.train.callback import ModelCheckpoint, CheckpointConfig

# 设置epoch_num数量
epoch_num = 5

# 设置模型保存参数
config_ck = CheckpointConfig(save_checkpoint_steps=1875, keep_checkpoint_max=10)

# 应用模型保存参数
ckpoint = ModelCheckpoint(prefix="lenet", directory="./lenet", config=config_ck)
model.train(epoch_num, dataset_train, callbacks=[ckpoint])

# 生成的CheckPoint文件如下
# lenet-graph.meta # 编译后的计算图
# lenet-1_1875.ckpt  # CheckPoint文件后缀名为'.ckpt'
# lenet-2_1875.ckpt  # 文件的命名方式表示保存参数所在的epoch和step数，这里为第2个epoch的第1875个step的模型参数
# lenet-3_1875.ckpt  # 表示保存的是第3个epoch的第1875个step的模型参数

• 3. 加载模型

• 要加载模型权重，需要先创建相同模型的实例，然后使用load_checkpoint和load_param_into_net方法加载参数
• load_checkpoint方法会把参数文件中的网络参数加载到字典param_dict中
• load_param_into_net方法会把字典param_dict中的参数加载到网络或者优化器中，加载后，网络的参数就是CheckPoint保存的

from mindspore import load_checkpoint, load_param_into_net

from mindvision.classification.dataset import Mnist
from mindvision.classification.models import lenet

# 将模型参数存入parameter的字典中，这里加载的是上面训练过程中保存的模型参数
param_dict = load_checkpoint("./lenet/lenet-5_1875.ckpt")

# 重新定义一个LeNet神经网络
net = lenet(num_classes=10, pretrained=False)

# 将参数加载到网络中
load_param_into_net(net, param_dict)
model = Model(net, loss_fn=net_loss, optimizer=net_opt, metrics={"accuracy"})

4. 模型验证

• 在上述模块把参数加载到网络中之后，针对推理场景，可以调用eval函数进行推理验证

# 调用eval()进行推理
download_eval = Mnist(path="./mnist", split="test", batch_size=32, resize=32, download=True)
dataset_eval = download_eval.run()
acc = model.eval(dataset_eval)

print("{}".format(acc))  # {'accuracy': 0.9866786858974359}

5. 用于迁移学习

• 针对任务中断再训练及微调 (Fine-tuning) 场景，可以调用train函数进行迁移学习

# 定义训练数据集
download_train = Mnist(path="./mnist", split="train", batch_size=32, repeat_num=1, shuffle=True, resize=32, download=True)
dataset_train = download_train.run()

# 网络模型调用train()继续进行训练
model.train(epoch_num, dataset_train, callbacks=[LossMonitor(0.01, 1875)])

九、推理与部署

• 推理与部署：模型导出 - 转化格式 - 部署与体验