yolov5网络结构学习

（注：原文链接是深入浅出Yolo系列之Yolov5核心基础知识完整讲解，我觉得这篇文章写的很好，所以自己手敲了一遍，并修改了很小一部分的细节，或者加了一些来自作者另一篇文章深入浅出Yolo系列之Yolov3&Yolov4&Yolov5核心基础知识完整讲解中的内容）
（更：参考yolov5深度可视化解析，从loss设计和anchor生成两方面深入理解yolov5的核心思想）

1. yolov5 网络架构

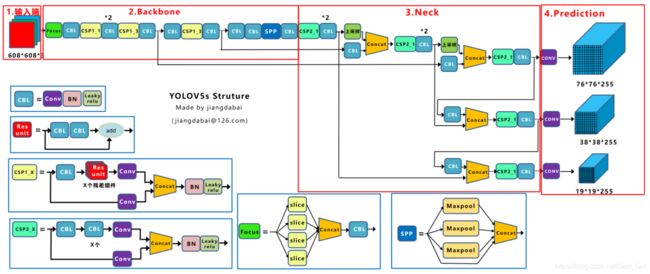
上图是yolov5s的网络结构，它是yolov5系列中深度最小、特征图宽度最小的网络。后面的m、l、x都是在此基础上不断加深、加宽的。

网络主要分为输入端、Backbone、Neck、Prediction四个部分。

它和yolov3主要不同的地方：

（1）输入端：Mosaic数据增强、自适应锚框计算、自适应图片缩放
（2）Backbone：Focus结构、CSP结构
（3）Neck：FPN+PAN结构
（4）Prediction：GIOU_Loss

下面从这四个方面入手进行比较，同时和yolov4进行对比。

2.输入端

（1）Mosaic数据增强

yolov5的输入端采用了和yolov4一样的Mosaic数据增强的方式。

Mosaic数据增强提出的作者也是来自yolov5团队的成员。它是采用4张图片，随机缩放、随机裁剪、随机排布的方式进行拼接，对于小目标的检测效果还是很不错的。

为什么要进行Mosaic数据增强呢？

在平时项目训练时，小目标的AP一般比中目标和大目标低得多。而coco数据集中也包含大量的小目标，但比较麻烦的是小目标的分布并不均匀。

首先看下小、中、大目标的定义：

可以看到小目标的定义是目标框的长宽0*0~32*32之间的物体。但是在coco中的分布是怎么样的呢？看下表：

在整体的数据集中，小、中、大目标的占比并不均衡。上表中，coco数据集中小目标占比达到41.4%，数量比中目标和大目标都要多，但是在所有的训练集的图片中，只有52.3%的图片有小目标而中目标和大目标的分布相对来说更加均匀一些。

针对这种状况，yolov4的作者采用了Mosaic数据增强的方式。

主要有几个优点：

• 丰富数据集：随机使用4张图片，随机缩放，再随机分布进行拼接，大大丰富了检测数据集，特别是随机缩放增加了很多小目标，让网络的鲁棒性更好。
• 减少GPU：可能会有人说，随机缩放，普通的数据增强也可以做，但作者考虑到很多人可能只有一个GPU，因此Mosaic增强训练时，可以直接计算4张图片的数据，使得Mini-batch大小并不需要很大，一个GPU就可以达到比较好的效果。

（2）自适应锚框计算

在yolo算法中，针对不同的数据集，都会有初始设定长宽的锚框。

在网络训练中，网络在初始锚框的基础上输出预测框，进而和真实框groundtruth进行比对，计算两者差距，再反向更新，迭代网络参数。

因此初始锚框也是比较重要的一部分，比如yolov5在coco数据集上初始设定的锚框：

在yolov3、yolov4中，训练不同的数据集时，计算初始锚框的值是通过单独的程序运行的。

但yolov5中，将此功能嵌入到代码中，每次训练时，自适应的计算不同训练集中的最佳锚框值。

当然，如果觉得计算的锚框效果不是很好，也可以在代码中将自动计算锚框功能关闭。

上面的代码在train.py中，store_true表示触发时为真，不触发则为假，所以随意传入一个值都会默认true，即开启noautoanchor，关闭自动计算锚框。

（3）自适应图片缩放

在常用的目标检测算法中，不同的图片长宽也不相同，因此常用的方式是将原始图片统一缩放到一个标准尺寸，在送入检测网络中。

比如yolo算法中常用416*416，608*608等尺寸，比如对下面800*600的图像进行缩放。

但yolov5代码中对此进行了改进，也是yolov5推理速度能够很快的一个不错的trick。

作者认为，在项目实际使用时，很多图片的长宽比不同，因此缩放填充后，两端的黑边大小都不同，而如果填充的比较多，则存在信息冗余，影响推理速度。

因此在yolov5的代码中datasets.py的letterbox函数进行了修改，对原始图像自适应的添加最少的黑边。

图像高度上两端的黑边变少了，在推理时，计算量也会减少，即目标检测速度会得到提升。

通过这种简单的改进，推理速度得到了37%的提升，可以说效果很明显。

但是如何进行计算的呢？

第一步：计算缩放比例

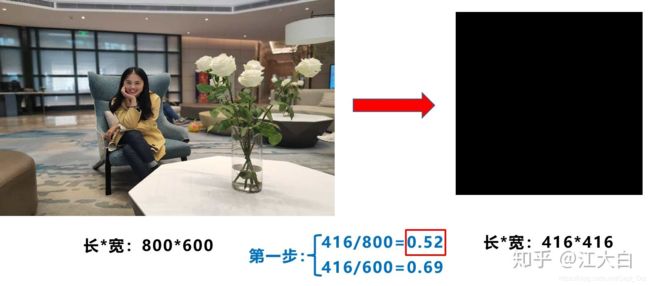
原始缩放尺寸是416*416，都除以原始图像的尺寸后，可以得到0.52和0.69两个缩放系数，选择小的缩放系数。

第二步：计算缩放后的尺寸

原始图片的长宽都乘以最小的缩放系数0.52，宽变成了416，而高变成了312。

第三步：计算黑边填充数值

将416-312=104，得到原本需要填充的高度。再采用numpy中np.mod取余数的方式，得到8个像素，再除以2，即得到图片高度两端需要填充的数值。

此外，需要注意的是：

• 这里图中填充的是黑色，即（0，0，0），而yolov5中填充的是灰色，即（114，114，114），都是一样的效果。
• 训练时没有采用缩减黑边的方式，还是采用传统填充的方式，即缩放到416*416大小。只是在测试、使用模型推理时，才采用缩减黑边的方式，提高目标检测，推理的速度。
• 为什么np.mod函数的后面用32？因为yolov5的网络经过5次下采样，而2的5次方，等于32。所以至少要去掉32的倍数，再进行取余。

3.Backbone

（1）Focus结构

源码如下：
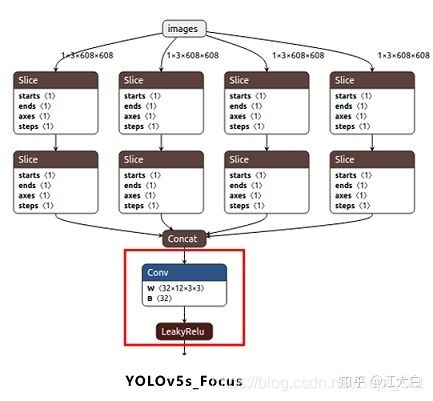
Focus结构如下，在yolov3、yolov4中并没有这个结构，其中比较关键是切片操作。

比如上图右边的切片示意图，4*4*3的图像切片后变成2*2*12的特征图。

以yolov5s的结构为例，原始608*608*3的图像输入Focus结构，采用切片操作，先变成304*304*12的特征图，再经过一次32个卷积核的卷积操作，最终变成304*304*32的特征图。

需要注意的是：yolov5s的Focus结构最后使用了32个卷积核，而其他三种结构，使用的数量有所增加。

（2）CSP结构

yolov4网络结构中，借鉴了CSPNet的设计思路，在主干网络中设计了CSP结构。

yolov5与yolov4不同点在于，yolov4中只有主干网络使用了CSP结构。

而yolov5中设计了两种CSP结构，以yolov5s网络为例，CSP1_X结构应用于Backbone主干网络，另一种CSP2_X结构则应用于Neck中。

可以看一下yolov4中的CSPNet——CSPDarknet53：

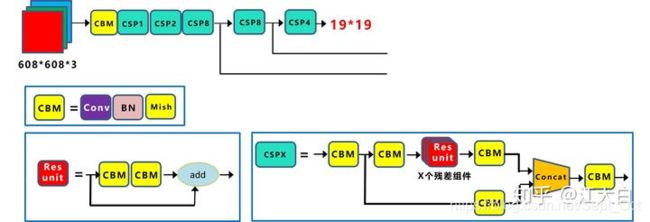
CSPDarknet53是在yolov3主干网络Darknet53的基础上，借鉴2019年CSPNet的经验，产生的Backbone结构，其中包含了5个CSP模块。

每个CSP模块前面的卷积核的大小都是3*3，stride=2，因此可以起到下采样的作用。

因为Backbone有5个CSP模块，输入图像是608*608，所以特征图变化的规律是：608->304->152->76->38->19

经过5次CSP模块后得到19*19大小的特征图。

而且，作者只在Backbone中采用了Mish激活函数，网络后面仍然采用Leaky_relu激活函数。

为什么要采用CSP模块呢？

CSPNet全称是Cross Stage Paritial Network，主要从网络结构设计的角度解决推理中计算量很大的问题。

CSPNet的作者认为推理计算过高的问题是由于网络优化中的梯度信息重复导致的。

因此采用CSP模块先将基础层的特征映射划分为两部分，然后通过跨阶段层次结构将它们合并，在减少了计算量的同时，可以保证准确率。

因此yolov4在主干网络Backbone采用CSPDarknet53网络结构，主要有三个方面的有点：

• 优点一：增强CNN的学习能力，使得在轻量化的同时保持准确性。
• 优点二：降低计算瓶颈
• 优点三：降低内存成本

4.Neck

yolov5现在的Neck和yolov4的一样，都采用FPN+PAN的结构，但在yolov5刚出来时，只使用了FPN结构，后面才增加了PAN结构，此外网络中其他部分也进行了调整。

先看一下yolov3中的Neck的FPN结构：

可以看到经过几次下采样，三个紫色箭头指向的地方，输出分别是76*76、38*38、19*19。

以及最后的Prediction中用于预测的三个特征图，①19*19*255，②38*38*255，③76*76*255。
【注：255表示80类别(1+4+80)*3=255】

我们将Neck部分用立体图画出来，更直观的看下两部分之间是如何通过FPN结构融合的。

如图所示，FPN是自顶向下的，将高层的特征信息通过上采样的方式进行传递融合的，得到进行预测的特征图。

而yolov4中Neck这部分除了使用FPN外，还在此基础上使用了PAN结构：

前面CSPDarknet53中讲到，每个CSP模块前面的卷积核都是3*3大小，步长为2，相当于下采样操作。

因此可以看到三个紫色箭头处的特征图是76*76、38*38、19*19。

以及最后的Prediction中用于预测的三个特征图，①76*76*255，②38*38*255，③19*19*255。

下面是Neck部分的立体图像，展示了两部分是如何通过FPN+PAN结构进行融合的。

和yolov3的FPN层不同，yolov4在FPN层的后面还添加了一个自底向上的特征金字塔。

其中，包含两个PAN结构。

这样结合操作，FPN层自顶向下传达强语义特征，而特征金字塔则自底向上传达强定位特征，两两联手，从不同的主干层对不同的检测层进行参数聚合，这样的操作确实很皮。

FPN+PAN借鉴的是18年CVPR的PANet，当时主要应用于图像分割领域，但Alexey将其拆分应用到yolov4中，进一步提高特征提取的能力。

不过这里需要注意几点：

注意一：

yolov3的FPN层输出的三个大小不一的特征图①②③直接进行预测

但yolov4的FPN层，只使用最后的一个76*76的特征图①，而经过两次PAN结构，输出预测的特征图②和③。

这里的不同也体现在cfg文件中：

比如yolov3.cfg最后三个yolo层：

第一个yolo层是最小的特征图19*19，mask=6,7,8，对应最大的anchor box。

第二个yolo层是中等的特征图38*38，mask=3,4,5，对应中等的anchor box。

第三个yolo层是最大的特征图76*76，mask=0,1,2，对应最小的anchor box。

而yolov4.cfg则恰恰相反：

第一个yolo层是最大的特征图76*76，mask=0,1,2，对应最小的anchor box。

第二个yolo层是中等的特征图38*38，mask=3,4,5，对应中等的anchor box。

第三个yolo层是最小的特征图19*19，mask=6,7,8，对应最大的anchor box。

注意点二：

原本的PANet网络的PAN结构中，两个特征图结合是采用shortcut操作，而yolov4中则采用concat（route）操作，特征图融合后的尺寸发生了变化。

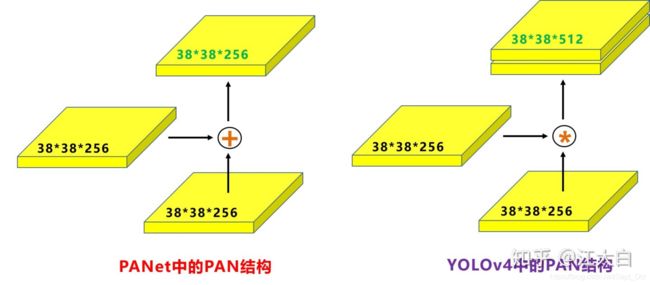
但如上面CSPNet结构中讲到，yolov5和yolov4的不同点在于：

yolov4的Neck结构中，采用的都是普通的卷积操作。而yolov5的Neck结构中，采用借鉴CSPNet设计的CSP2结构，加强网络特征融合的能力。

5.输出端

（1）Bounding box损失函数

目标检测任务的损失函数一般由Classification Loss（分类损失函数）和Bounding Box Regression Loss（回归损失函数）两部分组成。

Bounding Box Regression的Loss近些年的发展过程是：Smooth L1 Loss -> IOU Loss（2016）-> GIOU Loss（2019）-> DIOU Loss（2020）-> CIOU Loss（2020）

a.IOU_Loss

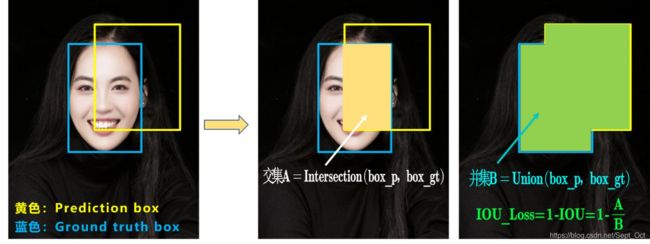
可以看到IOU的loss其实很简单，主要是交集/并集，但其实也存在两个问题。

问题1：即状态1的情况，当预测框和目标框不相交时，IOU=0，无法反映两个框距离的远近，此时损失函数不可导，IOU_Loss无法优化两个框不相交的情况。

问题2：即状态2和状态3的情况，当两个预测框大小相同，两个IOU也相同，IOU_Loss无法区分两者相交情况的不同。

因此2019年出现了GIOU_Loss来进行改进。

b.GIOU_Loss

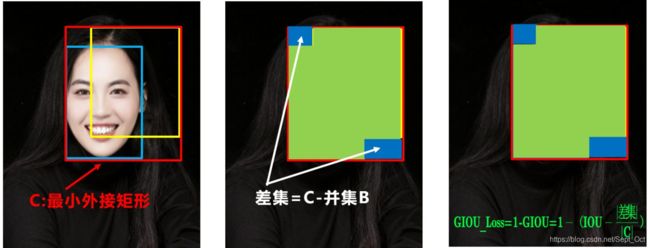
可以看到右图GIOU_Loss中，增加了相交尺度的衡量方式，缓解了单纯IOU_Loss时的尴尬。

但为什么仅仅说缓解呢？

因为还存在一种不足：

问题：状态1、2、3都是预测框在目标框内部且预测框大小一致的情况，这时预测框和目标框的差集都是相同的，因此这三种状态的GIOU值也都是相同的，这时GIOU退化成了IOU，无法区分相对位置关系。

基于这个问题，2020年AAAI又提出了DIOU_Loss。

c.DIOU_Loss

好的目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离、长宽比。

针对IOU和GIOU存在的问题，作者从两个方面进行考虑

一：如何最小化预测框和目标框之间的归一化距离？

二：如何在预测框和目标框重叠时，回归得更准确？

针对第一个问题，提出了DIOU_Loss（Distance_IOU_Loss）

DIOU_Loss考虑了重叠面积和中心点距离，当目标框包裹预测框的时候，直接度量两个框的距离，因此DIOU_Loss收敛得更快。

但就像前面好的目标框回归函数所说的，没有考虑到长宽比。

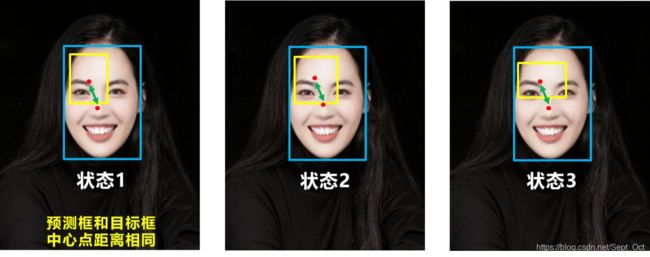
比如上面三种情况，目标框包裹预测框，本来DIOU_Loss可以起作用。

但预测框的中心点的位置都是一样的，因此按照DIOU_Loss的计算公式，三者的值都是相同的。

针对这个问题，又提出了CIOU_Loss，不得不说，科学总是在解决问题中，不断进步！

d.CIOU_Loss

CIOU_Loss和DIOU_Loss前面的公式都是一样的，不过在此基础上还增加了一个影响因子，将预测框和目标框的长宽比都考虑了进去。

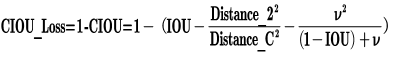
其中v是衡量长宽比一致性的参数，我们也可以定义为：

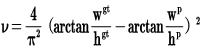
这样CIOU_Loss就将目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离、长宽比全都考虑进去了。

再来综合看下各个Loss函数的不同点：

IOU_Loss：主要考虑检测框和目标框重叠面积。

GIOU_Loss：在IOU的基础上，解决边界框不重合时的问题。

DIOU_Loss：在IOU和GIOU的基础上，考虑边界框中心点距离的信息。

CIOU_Loss：在DIOU的基础上，考虑边界框宽高比的尺度信息。

（存疑，求解答，）yolov4采用了CIOU_Loss的回归方式，而yolov5采用了GIOU_Loss作为Bounding_box的损失函数。

我查看了一下github上yolov4和yolov5的代码，似乎不是上述那样。(查看时间：2021.05.25)

yolov4(https://github.com/Tianxiaomo/pytorch-YOLOv4/blob/master/train.py)

yolov5(https://github.com/ultralytics/yolov5/blob/master/utils/loss.py)

（2）nms非极大值抑制

在目标检测的后处理过程中，针对很多目标框的筛选，通常需要nms操作。

因为CIOU_Loss中包含影响因子v，涉及groundtruth的信息，而测试推理时，是没有groundtruth的。

（存疑，求解答，）所以yolov4在DIOU_Loss的基础上采用DIOU_nms的方式，而yolov5中采用加权nms的方式。

nms是不是就是通过build_targets实现的呢？我查看了yolov4和yolov5的代码，如下：

yolov4(https://github.com/Tianxiaomo/pytorch-YOLOv4/blob/master/train.py)


yolov5(https://github.com/ultralytics/yolov5/blob/master/utils/loss.py)

可以看出，采用DIOU_nms，下方中间箭头的黄色部分，原本被遮挡的摩托车也可以检出。

在同样的参数情况下，将nms中IOU修改成DIOU_nms。对于一些遮挡重叠的目标，确实会有一些改进。

比如下面黄色箭头部分，原本两个人重叠的部分，在参数和普通的IOU_nms一致的情况下，修改成DIOU_nms，可以将两个目标检出。

虽然大多数状态下效果差不多，但在不增加计算成本的情况下，有稍微的改进也是好的。

6.yolov5四种网络结构的不同点

yolov5代码中的四种网络，和之前的yolov3，yolov4中的cfg文件不同，都是以yaml的形式来呈现。

而且四个文件的内容基本上都是一样的，只有最上方的depth_multiple和width_multiple两个参数不同。

（1）四种结构的参数

• yolov5s.yaml
  
• yolov5m.yaml
  
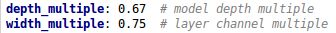
• yolov5l.yaml
  
• yolov5x.yaml
  
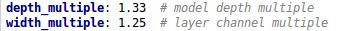
  四种结构就是通过上面的两个参数，来控制网络的深度和宽度。其中depth_multiple控制网络的深度，width_multiple控制网络的宽度。

（2）yolov5网络结构

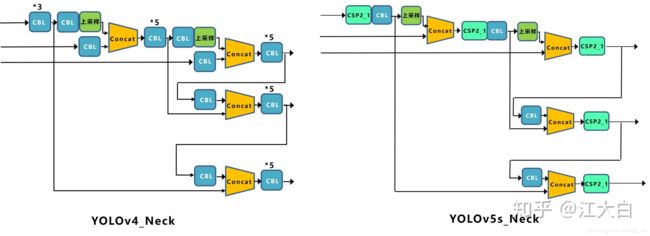
四种结构的yaml文件中，下方的网络架构代码都是一样的。

下图以backbone为例，理解如何控制网络的宽度和深度，yaml文件中的Head部分也是同样的道理。

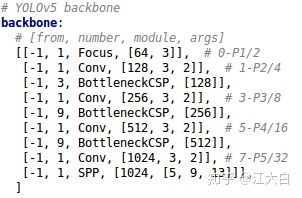
在对网络结构进行解析时，yolo.py中下方的这一行代码将四种结构的depth_multiple，width_multiple提取出，赋值给gd、gw。后面主要对gd、gw这两个参数进行讲解。

下面再细致地剖析下，看是如何控制每种结构的深度和宽度的。

（3）yolov5四种网络的深度

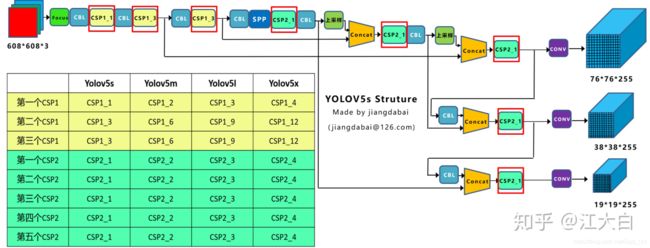
• 不同网络的深度

上图中包含两种CSP结构，CSP1和CSP2，其中CSP1结构主要应用于Backbone中，CSP2结构主要应用于Neck中。

需要注意的是，四种网络结构中每个CSP结构的深度都是不同的。

a.以yolov5s为例，第一个CSP1中，使用了1个残差组件，因此是CSP1_1。而在yolov5m中，则是增加了网络的深度，在第一个CSP1中，使用了两个残差组件，因此是CSP1_2。

而yolov5l中，同样的位置，则使用了3个残差组件，yolov5x中，使用了4个残差组件。

其余的第二个CSP1和第三个CSP1也是同样的道理。

b.在第二种CSP2结构中也是同样的方式，以第一个CSP2结构为例，yolov5s组件中使用了2*X=2*1=2个卷积，因为X=1，所以使用了1组卷积，因此是CSP2_1。

而yolov5m中使用了2组，yolov5l中使用了3组，yolov5x中使用了4组。

其他的四个CSP2结构，也是同理。

yolov5中，网络的不断加深，也在不断增加网络特征提取和特征融合的能力。

• 控制深度的代码

控制四种网络结构的核心代码是yolo.py中下面的代码，存在两个变量，n和gd。

我们将n和gd代入计算，看每种网络的变化结果。

• 验证控制深度的有效性

我们选择最小的yolov5s.yaml和中间的yolov5l.yaml两个网络结构，将gd(height_multiple)系数代入，看是否正确：

a.yolov5s.yaml

其中height_multiple=0.33，即gd=0.33，而n则由上面红色框中的信息获得。

以上面网络框图中的第一个CSP1为例，即上面的第一个红色框。n等于第二个数值3。

而gd=0.33，代入上面的公式，结果n=1。因此第一个CSP1结构内只有1个残差组件，即CSP1_1。

第二个CSP1结构中，n等于第二个数值9，而gd=0.33，代入上面的公式，结果n=3，因此第二个CSP1结构中有3个残差组件，即CSP1_3。

第三个CSP1结构也是同理。

b.yolov5l.yaml

其中，height_multiple=1，即gd=1

和上面的计算方式相同，第一个CSP1结构中，n=3，代入代码中，结果n=3，因此为CSP1_3。

下面第二个CSP1和第三个CSP1结构都是同样的原理。

（4）yolov5四种网络的宽度

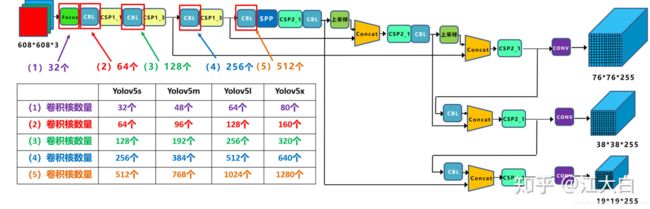
• 不同网络的宽度

如上图表格中所示，四种yolov5结构在不同阶段的卷积核的数量是不一样的，因此也直接影响了卷积后特征图的第三维度，即厚度，也就是网络的宽度。

a.以yolov5s结构为例，第一个Focus结构中，最后卷积操作时，卷积核的数量是32个，因此经过Focus结构，特征图的大小变成304*304*32。

而yolov5m的Focus结构中的卷积操作使用了48个卷积核，因此Focus结构后的特征图变成304*304*48。yolov5l，yolov5x也是同样的原理。

b.第二个卷积操作时，yolov5s使用了64个卷积核，因此得到的特征图是152*152*64。而yolov5m使用96个特征图，因此得到的特征图是152*152*96。yolov5l，yolov5x也是同理。

c.后面三个卷积下采样操作也是同样的道理。

四种不同结构的卷积核的数量不同，这也直接影响网络中，比如CSP1，CSP2等结构，以及各个普通卷积，卷积操作时的卷积核数量也同步在调整，影响整体网络的计算量。

卷积核的数量越多，特征图的厚度，即宽度，也即网络提取特征的学习能力也越强。

• 控制网络宽度的代码

在yolov5的代码中，控制宽度的核心代码时yolo.py文件里面的这一行：

它所调用的子函数make_divisible的功能是：

• 验证控制宽度的有效性

我们还是选择最小的yolov5s和中间的yolov5l两个网络结构，将width_multiple系数代入，看是否正确。

a.yolov5s.yaml

其中width_multiple=0.5，即gw=0.5。

以第一个卷积下采样为例，即Focus结构中下面的卷积操作。

按照上面Backbone的信息，我们知道Focus中，标准的c2=64，而gw=0.5，代入c2的计算公式，最后结果=32。即yolov5的Focus结构中，卷积下采样操作的卷积核数量为32个。

再计算后面的第二个卷积下采样操作，标准c2的值=128，gw=0.5，代入c2的计算公式，最后的结果=64，也是正确的。

b.yolov5l.yaml

其中width_multiple=1，即gw=1，而标准的c2=64，代入上面c2的计算公式中，可以得到yolov5的Focus结构中，卷积下采样操作的卷积核的数量为64个，而第二个卷积下采样的卷积核操作是128个。

另外的三个卷积下采样操作，以及yolov5m，yolov5x结构也是同样的计算方式。

7.yolov5中的loss计算

yolov5的loss设计和前yolo系列差别比较大的地方就是正样本anchor区域计算。loss的计算，核心在于如何得到所需的target。

在yolov3中，其正样本区域也就是anchor匹配策略比较粗暴：保证每个gt bbox一定有一个唯一的anchor进行对应，匹配规则就是IOU最大，并且某个gt一定不可能在三个预测层的某几层上同时进行匹配。不考虑一个gt bbox对应多个anchor的场合，也不考虑anchor是否设定合理。不考虑一个gt bbox对应多个anchor的场合的设定会导致整体收敛比较慢。

在诸多论文研究中表明，例如FCOS和ATSS：增加高质量正样本anchor可以显著加速收敛。

yolov5也采用了增加正样本anchor数目的做法来加速收敛，这其实也是yolov5在实践中收敛速度非常快的原因。其核心匹配规则为：

• 对于任何一个输出层，抛弃了基于max iou匹配的规则，而是直接采用shape规则匹配，也就是该bbox和当前层的anchor计算宽高比，如果宽高比例大于设定阈值，则说明该bbox和anchor匹配度不够，将该bbox过滤暂时丢掉，在该层预测中认为是背景；
• 对于剩下的bbox，计算其落在哪个网格内，同时利用四舍五入规则，找出最近的两个网格，将这三个网格都认为是负责预测该bbox的，可以发现粗略估计正样本数相比前yolo系列，至少增加了三倍
  
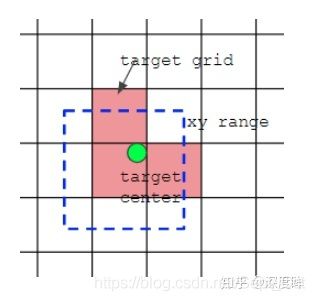
  如上图所示，绿点表示该bbox中心，现在需要额外考虑其2个最近的邻域网格也作为该bbox的正样本anchor。从这里可以发现，bbox的xy回归分支的取值范围不再是0 ~ 1，而是-0.5 ~ 1.5（0.5是网格中心偏移，为什么是这个范围？），因为跨网格预测了。

为了方便理解，可以看下图：

三张图表示：

• 第一张，大输出特征图，stride=8，检测小物体
• 第二张，中等尺度特征图，stride=16，检测中尺度物体
• 第三张，小尺度特征图，stride=32，检测大尺度物体

其中，红色bbox表示该预测层中的gt bbox，黄色bbox表示该层对应位置的正样本anchor。第一幅图是大输出特征图，只检测小物体，所以人那个bbox标注被当作背景了，并且有三个anchor进行匹配了，其中包括当前网格位置anchor和两个最近邻域anchor。

yolov5不同于yolov3和v4：

• 其gt bbox可以跨层预测，即有些bbox在多个预测层都算正样本
• 其gt bbox的匹配数范围从3-9个，明显增加了很多正样本（3是因为多引入了两个邻居）
• 有些gt bbox由于和anchor匹配度不高，而变成背景

可能存在的问题是：增加正样本虽然可以加速收敛，但是也引入了很多低质量的anchor，有待考究。

结合代码分析yolov5的compute_loss函数：

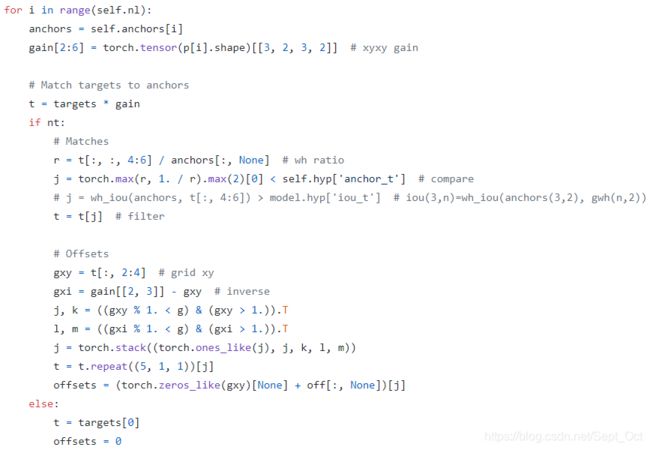
（1）build_targets

build_targets函数用于选择计算loss函数所需要的target。其大概流程为：

• 将targets重复三遍（3=层anchor数目），也就是将每个gt bbox复制变成独立的3份，方便和每个位置的3个anchor单独匹配。
  
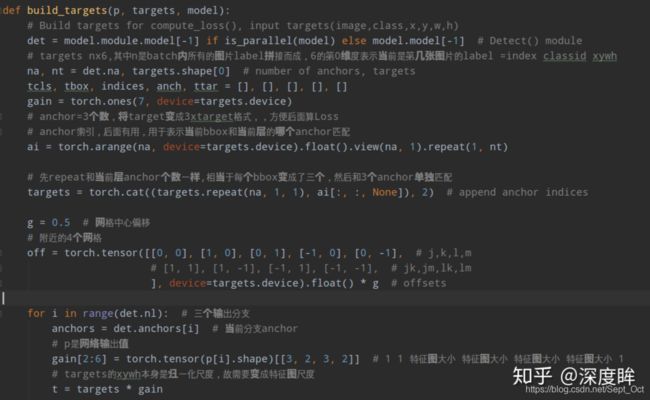
• 对每个输出层单独匹配。首先将targets变成anchor尺度，方便计算；然后将target的wh shape和anchor的wh计算比例，如果比例过大，则说明匹配度不高，将该bbox过滤，在当前层认为是bg。
  
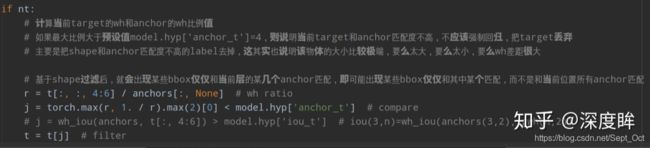
• 计算最近的2个邻域网格
  
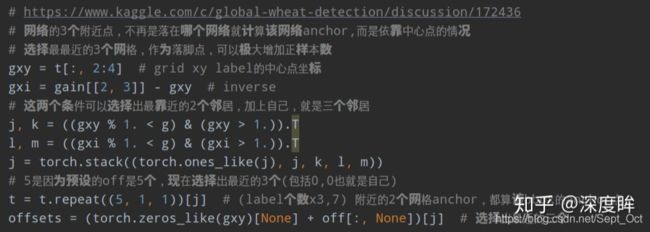
• 对每个bbox找出对应的正样本anchor，其中包括，b表示当前bbox属于batch内部的第几张图片，a表示当前bbox和当前层的第几个anchor匹配上，gi/gj是对应的负责预测该bbox的网格坐标，gxy是不考虑offset或者说yolov3里面设定的该bbox的负责预测网格，gwh是对应的归一化bbox wh，c是该bbox类别
  
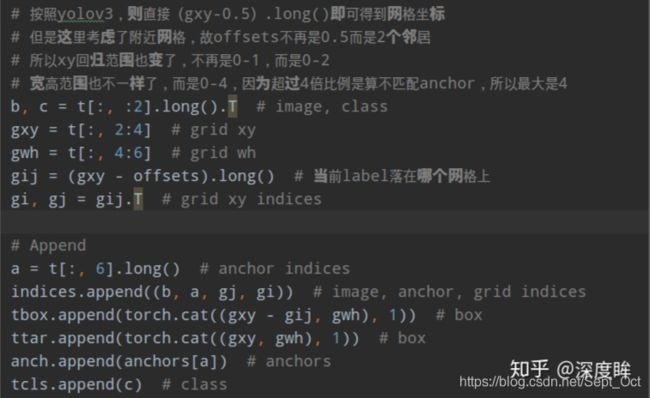
  由于其采用了跨网格预测，故预测输出不再是0 ~ 1，而是-1 ~ 1，加上offset偏移，则为-0.5 ~ 1.5；并且由于shape过滤规则，wh预测输出也不再是任意范围，而是0 ~ 4。

从上述可以发现：在任何一预测层，将每个bbox复制成跟anchor个数一样多的数目，然后将bbox和anchor一一对应计算，去除不匹配的bbox，然后对原始中心点网格坐标扩展两个邻域像素，增加正样本anchor。有个细节需要注意，前面shape过滤时是不考虑bbox的xy坐标的，也就是说，bbox的wh是和所有anchor匹配的，会导致找到的邻域也相当于进行了shape过滤规则，故对于任何一个输出层，如果该bbox保留，那么至少有3个anchor进行匹配，并且保留的3个anchor shape是一样大的。即保留的anchor在不考虑越界情况下是3或者6或者9。

（2）loss计算

有了上述数据，计算loss就非常容易了。

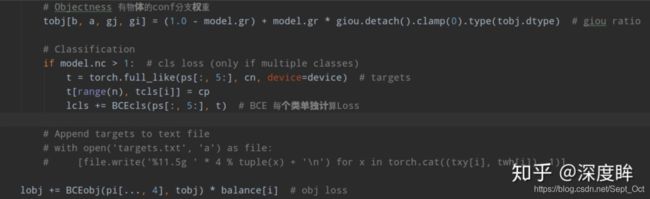
BCEcls = nn.BCEWithLogitsLoss(pos_weight=torch.Tensor([h['cls_pw']])).to(device)
BCEobj = nn.BCEWithLogitsLoss(pos_weight=torch.Tensor([h['obj_pw']])).to(device)

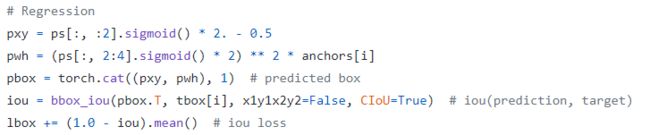
设置了正样本区域权重，cls和conf分支都是bce loss，xywh分支直接采用giou loss（疑惑，下图中不是ciou loss么？）

注意：

pwh = (ps[:, 2:4].sigmoid() * 2) ** 2 * anchors[i]  # wh

其没有采用exp操作，而是直接乘上anchors[i]。

类似fcos和yolov2，虽然引入了大量正样本anchor，但是不同anchor和gt bbox匹配度是不一样，预测框和gt bbox的匹配度也不一样，如果权重设置一样肯定不是最优的，故作者将预测框和bbox的giou作为权重乘到conf分支，用于表征预测质量。