CSK与KCF算法推导（六）

  本文是CSK与KCF算法推导的第六篇，主要介绍HOG特征提取与多通道计算。

• CSK与KCF算法推导（一）——DFT、相关运算和循环卷积
• CSK与KCF算法推导（二）——带核函数的岭回归问题求解
• CSK与KCF算法推导（三）——算法主体部分推导
• CSK与KCF算法推导（四）——从一维推广到二维
• CSK与KCF算法推导（五）——具体实现细节
• （本文）CSK与KCF算法推导（六）——HOG特征提取与多通道计算

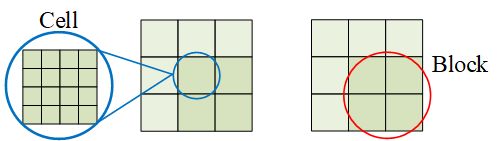
边缘特征提取

  采用 [-1，0，1] 的滤波模版求原始图像的水平和垂直方向的梯度。滤波模版的Anchor位于滤波模版的中心。求边缘的像素的梯度时，对原始图像的 边界有一个扩展的操作，作者采用的是镜像扩展，这样一来边缘像素的梯度值均为0。

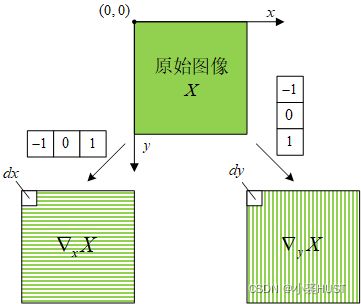
方向图与强度图

  在得到$x$方向的梯度图和$y$方向的梯度图之后，我们就得到了原始图像中每个像素点的梯度向量$(dx,dy)$，将这些梯度向量转换成模$r$与方向角$\alpha$进行表示，用于生成方向梯度直方图（Histogram of Oriented Gradient，HOG）。
  HOG的每个bin代表一个角度，bin的数量是有限的，所以需要对方向角进行量化（离散化），比如我们在[0,180°)分9个方向区间，每个方向区间为20°。
  在一个单位圆上，我们可以用“单位基准向量”来划分，如下图中的左图。对于某一个梯度向量$(dx,dy)$，我们不需要求出它具体的方向角，而只要判断它落在哪个区间内就行。

  求梯度向量和单位基准向量的内积，可以得到梯度向量在基准向量上的投影，只要找到投影最大的方向，就能确定这个梯度向量所在的方向区间。
  对应于左图的基准向量分布方式，我们可以画出实际的方向区间分布图，如上图中的右图所示。
  如果我们将方向角相差180°的梯度向量看作是同一方向，那么总共就有9个方向区间；反之，就有18个方向区间，如下图所示。这样两种不同的划分方式就能够得到两种不同的HOG。

  其中一个HOG有9个bin，另一个是18个bin，在生成直方图之前，我们可以先准备好它们对应的方向图和强度图，生成HOG就是要把梯度向量的模累加到对应的bin里面去。

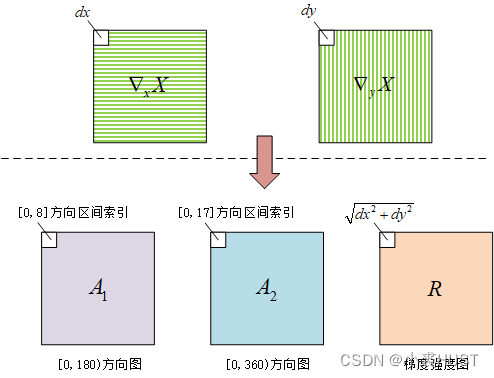
生成直方图

  生成直方图并不是全局的图像生成一个直方图，而是将图像分为一个个Cell，生成局部的直方图。如上图中所示，原始图像被分为一个个4×4的Cell，在每个Cell中做直方图统计。
  在一个Cell中做直方图统计最经典的做法应该是将梯度强度按照向它相邻的两个基准向量分解，然后将梯度强度值 按比例分配到对应的两个bin里。但在我们这里没有计算具体的梯度方向角，所以生成HOG的方式和经典的方式有点不同。

每个Cell都会对其周围的Cell生成的直方图有贡献

  将位于中心的Cell等分为左上、左下、右上、右下四部分。位于左上部分的梯度向量，它们会按照一定的比例系数分别为中心Cell、左方、上方、左上方的Cell对应的直方图产生贡献，其余三个部分也是类似。就这样，一个Cell中的梯度向量，会对共9个直方图（算上它自身对应的直方图）产生贡献。

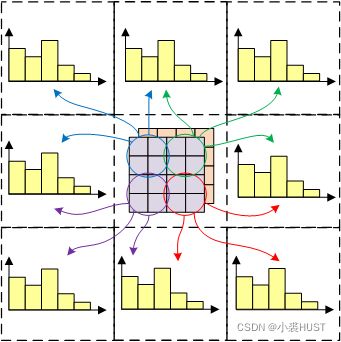
  如果一个Cell是在边界上的话，那些超出边界的地方就不去考虑了。具体是什么样的贡献呢？以Cell中的右下部分为例。

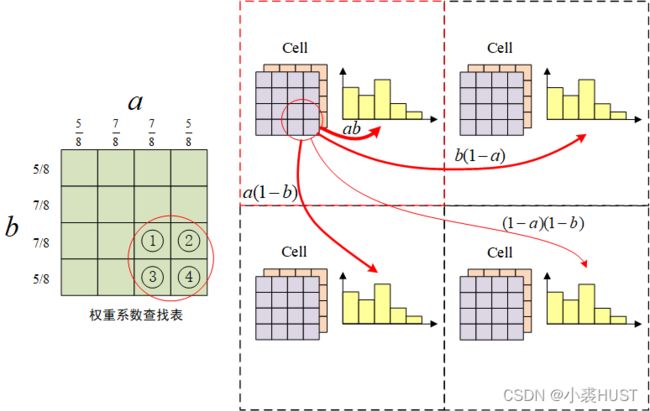
  比如①号位置的梯度向量的两个系数$a=b=\frac{5}{8}$，这一梯度向量的强度按照四个比例系数$ab$、$b(1-a)$、$a(1-b)$、$(1-a)(1-b)$、分到四个直方图相应的bin中。
$$\left(a+(1-a)\right)\left(b+(1-b)\right)=ab+a(1-b)+(1-a)b+(1-a)(1-b)=1$$
  作者这么做最直观的一个结果是什么呢？

每个HOG直方图是由扩展的Cell生成的

  每个Cell都以原来的Cell为中心，向外将边长扩展为原来的两倍。每个梯度向量的强度按照权重系数与对应的方向图，累加到直方图上。越靠近Cell中心的梯度向量权重系数越大，最大为$49/64$，最小为$1/64$。

特征图

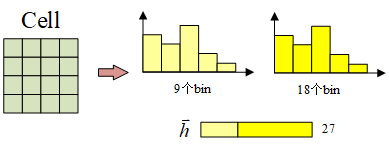
  根据[0,180°)和[0,360°)的方向图，同一个Cell能够得到两个HOG直方图，把它们拼起来就能得到一个长度为27的向量$h$。

  记原始图像有$M$行$N$列，$M$和$N$都能被4整除。将原始图像划分为一个个Cell之后，能够得到$P$行$Q$列的Cell，每个Cell对应一个27维的向量。所以此时的特征图就是三维的结构，相当于是多通道的图像，每一幅图都是$P\times Q$的大小，总共有27个通道。

归一化

  归一化的方式和经典的HOG算法是类似的。将相邻的四个Cell组成一个Block，不同的Block之间有重叠。但也有一些细微的不同。

  为了方便说明一些问题，先约定一些记号。上面的9个Cell中，有四个Cell分别标记为①、②、③、④，有四个互相部分重叠的Block分别记为Ⅰ、Ⅱ、Ⅲ、Ⅳ。

经典做法

  经典的做法是逐Block生成归一化的向量。比如Block Ⅳ，将Block Ⅳ里的四个Cell对应的27维向量拼成108维的向量，然后将这一向量的每个分量除以它的模长。

  一般来说有多少个Block就有多少个这样的108维向量。像这里以四个Cell为一个Block，并且有重叠，那么总共就能有$(P-1)\times (Q-1)$个Block。

实际做法

  而作者实际采用的归一化的方式和上面说的不同。作者采用的是逐Cell归一化。首先，求归一化采用的模长就不一样。在Block Ⅳ里，先将每个Cell的9维向量拿出来拼成一个36维的向量$h$，这里的9维向量就是前面的通过[0,180)的方向图生成的9个bin的直方图。

  然后计算这个向量的长度作为后面归一化的分母。
$$r(\mathrm{I}\mathrm{V})=\sqrt{\sum _{i=0}^{36}h{(i)}^2}$$
  用同样的方式能够计算另外三个Block对应的向量长度$r(\mathrm{I})$、$r(\mathrm{I}\mathrm{I})$、$r(\mathrm{I}\mathrm{I}\mathrm{I})$，对于同一个Cell ①，采用四种分母进行归一化，然后构成一个108维的向量。

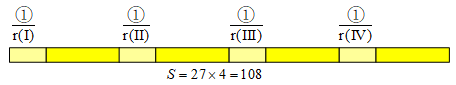
  为什么这里用来归一化的分母不是整个向量的模长呢？如果单看前面9维的话，实际上前面9维的归一化方式和经典的做法是一样的，区别在于结果存放的方式。经典做法中，结果按照Block组织，一个Block里的Cell组成一个新的向量；而这里只是将结果按照Cell进行组织，同一个Cell采用不同的归一化方式形成一个新的向量。
  而后面18维只是做了一个双向的统计，9维直方图里的一个bin放到18维直方图里，分成了两个bin。众所周知：
$$(a+\mathrm{b}{)}^2\ge a^2+b^2$$
  所以对于剩下18维的向量来说，它的二范数肯定比前面9维向量的二范数小。自然这剩下的18维向量也可以用前面9维向量的长度来“归一化”，归一化向量模长小于等于1。
  作者这么做也在一定程度上减少了运算量，而且能够逐Cell遍历，不需要逐Block时的回溯，便于程序编写。（上图中108维向量实际的排列并不是图中的排列方式，而是前面四组9维向量，后面紧跟着4组18维向量，但这个不影响对计算过程的理解）。

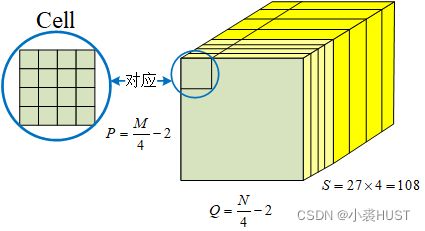
  前面生成直方图的过程中，边界的Cell因为无法再想边界外扩展，所以这些边界的Cell生成的直方图是有“缺陷”的。所以在归一化的过程中，直接就不考虑边界的Cell了。最终得到的特征图就会是上面这个样子。

主成分分析

  108个通道的特征图确实太大了，所以需要降维。经典的主成分分析的方式是，将每个通道的图像打平，变成108个一维向量，然后取均值，求用协方差矩阵特征值并从大到小排列，来得到基变换矩阵，最后得到降维后的结果。

  而作者这里的做法则是利用几个通道内在的关联性直接合并。9维和18维的向量分队把对应的分量相加，再乘以一个系数$\eta$或$\gamma$，最后再把四个18维的向量求和得到4个结果加在后面，形成31维的特征向量。

添加LAB特征

  最后就是把每个通道的特征图拉平，得到一维的行向量，然后按列排布得到二维的特征图。最后还可以选择是否要加上LAB颜色特征，实际上就是多一个图像通道而已。作者这里将图像拉平，我猜想主要目的就是用OpenCV里的push_back函数增加一个通道的特征。
  我一开始以为这里将图像拉平之后，后面就可以按照一维的方式处理每幅图像了，但实际上后面处理过程中还是需要将每幅图像恢复成二维去处理。也只有进行二维的处理才能获取样本在二维空间的密集采样。

多通道计算的可加性

  关于多通道的计算，一开始最让我疑惑的是，多通道的训练样本，该生成怎样的训练标签？是不是每个通道都需要生成一个高斯模板作为训练标签？后来再回想了一下训练的过程发现并不是这样的。
$$\alpha ={\left(K+\lambda I\right)}^{-1}y$$
  把问题放到对偶空间后，我们就只需要关注$K$矩阵的计算就好了。$K$矩阵是高维空间（特征空间）的的Gram矩阵，回顾第三篇文章可以发现，不管是采用多项式核还是高斯核，它们都离不开计算原始样本的Gram矩阵。就是计算每个训练样本自己和自己，自己和其他训练样本的内积。

  就比如现在有三个通道，如果孤立地去看，每个$X$矩阵中的每一行是一个样本，总共有“$3\times X$矩阵高度”个样本。
  但实际上不同通道之间是有关联性的，就比如每个通道的第一行，都表示没有发生移位的样本。我们可以把那些位移相同的样本级联起来构成一个更长的样本向量，让每个样本向量中包含多通道特征。这样就能将多通道样本归结到一个Gram矩阵。

  这和我们前面单通道的计算就联系起来了。

这有点像是在引入核技巧之前又引入了一个“小核技巧”。

  引入核函数最大的好处就是将原来的样本映射到了高维的特征空间，而这里引入多通道，有没有像是把样本先提高一点维度，然后再提高到更高维度的特征空间呢？这样去想就使得多通道的计算有了较强的可解释性。

  观察上面的计算过程可以发现，$G$矩阵就是三个通道计算得到的$G$矩阵对应位置的元素直接相加。

公式推导

  下面进行相关的公式推导，推导仍旧是针对一维样本。假设$x_1$、$x_2$、$x_3$分别是三个通道的列向量样本。然后我们把它们拼接起来。
$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$
  计算$K^{x{x}^{\prime }}$：
$$K^{x{x}^{\prime }}=\exp \left(-\frac{1}{{\sigma }^2}\left({\Vert x\Vert }^2+{\Vert x^{\prime }\Vert }^2+2x^T{x}^{\prime }\right)\right)$$
$$=\exp \left(-\frac{1}{{\sigma }^2}\left({\Vert x\Vert }^2+{\Vert x^{\prime }\Vert }^2+2{x_1}^T{x_1}^{\prime }+2{x_2}^T{x_2}^{\prime }+2{x_3}^T{x_3}^{\prime }\right)\right)$$
$$=\exp \left(-\frac{1}{{\sigma }^2}\left({\Vert x\Vert }^2+{\Vert x^{\prime }\Vert }^2+2\sum _{i=1}^3{\mathcal{F}}^{-1}({\hat{x}}_i\odot {\hat{x}}_i^{\prime \ast })\right)\right)$$
$$=\exp \left(-\frac{1}{{\sigma }^2}\left({\Vert x\Vert }^2+{\Vert x^{\prime }\Vert }^2+2{\mathcal{F}}^{-1}\sum _{i=1}^3({\hat{x}}_i\odot {\hat{x}}_i^{\prime \ast })\right)\right)$$
  最后一步的计算用了傅立叶变换的线性性质。