python实现简易动态贝叶斯网络的推断

Genle上构建的动态贝叶斯网络

动态贝叶斯网络构建参考的b站某个搬运的国外视频


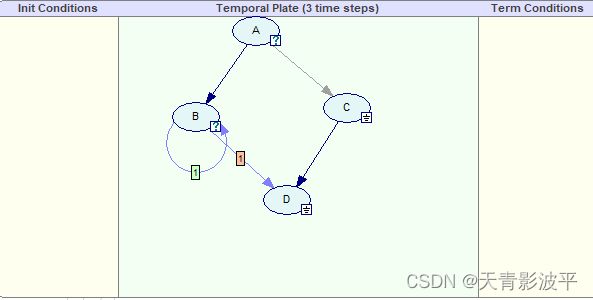
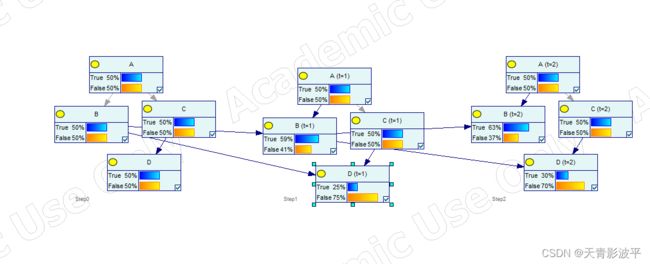
看完这个展开后的图，我决定自己试试用python实现这样一个简易动态贝叶斯网络。

python实现动态贝叶斯网络

具体的贝叶斯网络知识网上有很多，用的都是pgmpy，大概步骤都是
1）定义贝叶斯网络的节点和边；
2）定义根节点先验概率和其他节点条件概率
3）将条件概率cpd和网络关联
4）完成需要的推理
下面上代码（非专业人员，很多地方写的不好，见谅，欢迎提出宝贵意见和想法）

from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
# 定义贝叶斯网络结构,不同时刻贝叶斯网络不一样，假设每个时刻结构已知，设置为3个时间步
t=3
DBN= [BayesianNetwork() for _ in range(t+1)]
#条件概率
cpd = {}
for k in ['A','B','C','D']:#节点集合
    cpd.update({k:[]})

#对时间遍历，定义不同时刻的图模型，条件概率，并关联条件概率表
for i in range(0,t):
    cpd['A'].append(TabularCPD(variable='A' + str(i), variable_card=2, values=[[0.5], [0.5]]))#先验时序节点定义
    if i == 0:
        cpd['B'].append(TabularCPD(variable='B' + str(i), variable_card=2, values=[[0.5, 0.5], [0.5, 0.5]],
                                   evidence=['A' + str(i)], evidence_card=[2]))

        cpd['C'].append(TabularCPD(variable='C' + str(i), variable_card=2, values=[[0.5, 0.5], [0.5, 0.5]],
                                   evidence=['A' + str(i)], evidence_card=[2]))
        cpd['D'].append(TabularCPD(variable='D' + str(i), variable_card=2, values=[[1., 0.], [0., 1.]],
                                   evidence=['C' + str(i)], evidence_card=[2]))
        DBN[i] = BayesianNetwork([('A'+str(i), 'B'+str(i)), ('A'+str(i), 'C'+str(i)), ('C'+str(i), 'D'+str(i))])

        for k in ['A', 'B', 'C', 'D']:#对节点进行遍历
            DBN[i].add_cpds((cpd[k][i]))
        print(DBN[i].check_model())

        infer = VariableElimination(DBN[i])
        for k in ['B']:#待推断的并且作为下一个时刻节点输入的根节点结合
            temp= infer.query(variables=[k+str(i)])
            print(k+str(i),[[temp.values[0]], [temp.values[1]]])
            cpd[k][i] = TabularCPD(variable=k+str(i), variable_card=2,
                                   values=[[temp.values[0]], [temp.values[1]]])#将其更新为先验概率，即下一个时刻的根节点概率

    if i >0:
        cpd['B'].append(TabularCPD(variable='B' + str(i), variable_card=2, values=[[0.625, 0.3,0.6,0.1], [0.375,0.7,0.4,0.9]],
                                   evidence=['A' + str(i),'B' + str(i-1)], evidence_card=[2,2]))
        print(cpd['B'][1])
        cpd['C'].append(TabularCPD(variable='C' + str(i), variable_card=2, values=[[0.5, 0.5], [0.5, 0.5]],
                                   evidence=['A' + str(i)], evidence_card=[2]))
        cpd['D'].append(TabularCPD(variable='D' + str(i), variable_card=2, values=[[1,1,1,0], [0,0,0,1]],
                                   evidence=['C' + str(i),'B' + str(i-1)], evidence_card=[2,2]))
        DBN[i] = BayesianNetwork(
            [('A' + str(i), 'B' + str(i)), ('A' + str(i), 'C' + str(i)), ('C' + str(i), 'D' + str(i)),('B' + str(i-1), 'B' + str(i)),('B' + str(i-1), 'D' + str(i))])
        #DBN[i].add_node('B' + str(i-1))
        #DBN[i].add_edge(('B' + str(i-1), 'B' + str(i)),('B' + str(i-1), 'D' + str(i)))#在初始贝叶斯模型上更新模型
        #print(DBN[i].nodes)
        for k in ['A', 'B', 'C', 'D']:#对节点进行遍历
            DBN[i].add_cpds((cpd[k][i]))
        for k in ['B']:  # 待推断的并且作为下一个时刻节点输入的根节点结合
            DBN[i].add_cpds((cpd[k][i-1]))
        print(DBN[i].check_model())

        infer = VariableElimination(DBN[i])
        for k in ['B']:#待推断的并且作为下一个时刻节点输入的根节点结合
            temp = infer.query(variables=[k + str(i)])
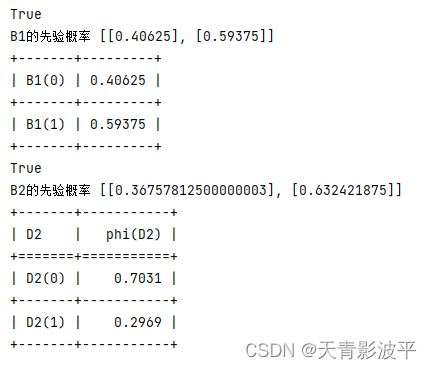
            print(k+str(i)+'的先验概率',[[temp.values[0]], [temp.values[1]]])
            cpd[k][i] = TabularCPD(variable=k+str(i), variable_card=2,
                                   values=[[temp.values[0]], [temp.values[1]]])#将其更新为先验概率，即下一个时刻的根节点概率
infer = VariableElimination(DBN[2])
temp = infer.query(variables=['D2'])
print(temp)

推断的概率和用软件算的应该一样，不过重要度计算和参数估计按我这样写应该不太行。