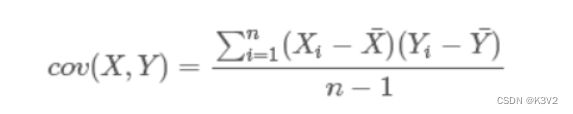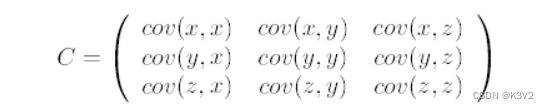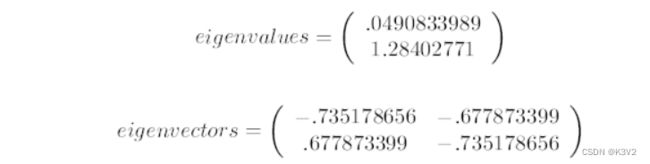PCA算法原理及python实现
【原理】PCA算法原理
1.PCA算法
PCA(principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据压缩算法。在PCA中,数据从原来的坐标系转换到新的坐标系,由数据本身决定。转换坐标系时,以方差最大的方向作为坐标轴方向,因为数据的最大方差给出了数据的最重要的信息。第一个新坐标轴选择的是原始数据中方差最大的方法,第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程,重复次数为原始数据的特征维数。
通过这种方式获得的新的坐标系,我们发现,大部分方差都包含在前面几个坐标轴中,后面的坐标轴所含的方差几乎为0,。于是,我们可以忽略余下的坐标轴,只保留前面的几个含有绝不部分方差的坐标轴。事实上,这样也就相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,也就实现了对数据特征的降维处理。
那么,我们如何得到这些包含最大差异性的主成分方向呢?事实上,通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值及特征向量,选择特征值最大(也即包含方差最大)的N个特征所对应的特征向量组成的矩阵,我们就可以将数据矩阵转换到新的空间当中,实现数据特征的降维(N维)。
说到这里,可能会疑惑,为什么要计算数据矩阵的协方差矩阵呢?
回顾一下,协方差的意义:计算数据各维度之间的相关性、度量两个随机变量关系的统计量、度量各个维度偏离其均值的程度。而协方差矩阵则是,其每一个因子都可以视为两个不同随机变量的关系,也就是好多协方差凑在一起形成了协方差矩阵,用来衡量各个变量之间的紧密程度。计算协方差的公式:
PCA算法的实质就是在能尽可能好的代表原特征的情况下,将原特征进行线性变换、映射至低纬度空间中。
【原理】PCA实例
2.PCA实例
现在假设有一组数据如下:
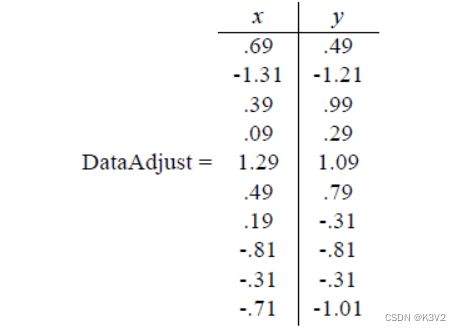
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。可以这样认为,有10篇文档,x是10篇文档中“learn”出现的TF-IDF,y是10篇文档“study”出现的TF-IDF。
第一步,分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,那么一个样例减去均值后即为(0.69,0.49),得到
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是
这里只有x和y,求解得
对角线上分别是x和y的方差,非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增,另一个也增;小于0表示一个增,一个减。如果x和y是统计独立的,那么二者之间的协方差就是0;但是协方差是0,并不能说明x和y是独立的。协方差绝对值越大,两者对彼此的影响越大,反之越小。协方差是没有单位的量,因此,如果同样的两个变量所采用的量纲发生变化,它们的协方差也会产生树枝上的变化。
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为,这里的特征向量都归一化为单位向量。
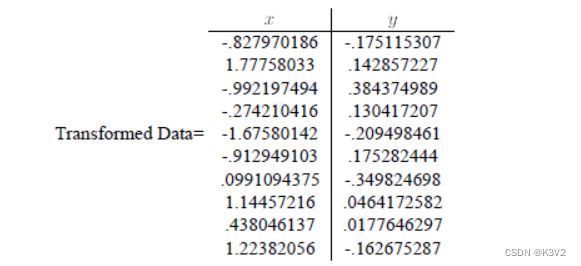
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。这里特征值只有两个,我们选择其中最大的那个,这里是1.28402771,对应的特征向量是(-0.677873399, -0.735178656)T。
第五步,将样本点投影到选取的特征向量上。假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(mn),协方差矩阵是nn,选取的k个特征向量组成的矩阵为EigenVectors(nk)。那么投影后的数据FinalData为![]()
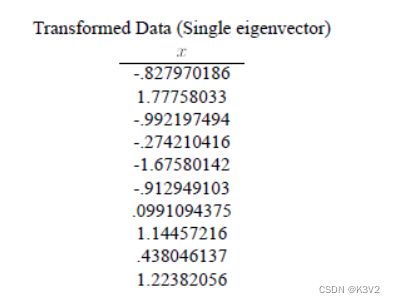
这里是: FinalData(101) = DataAdjust(10*2矩阵) x 特征向量(-0.677873399, -0.735178656)T
得到的结果是:
这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
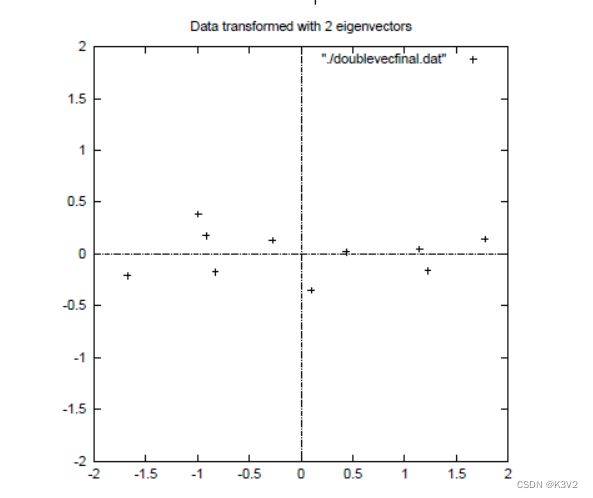
上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征,该特征基本上代表了这两个特征。上述过程如下图2描述: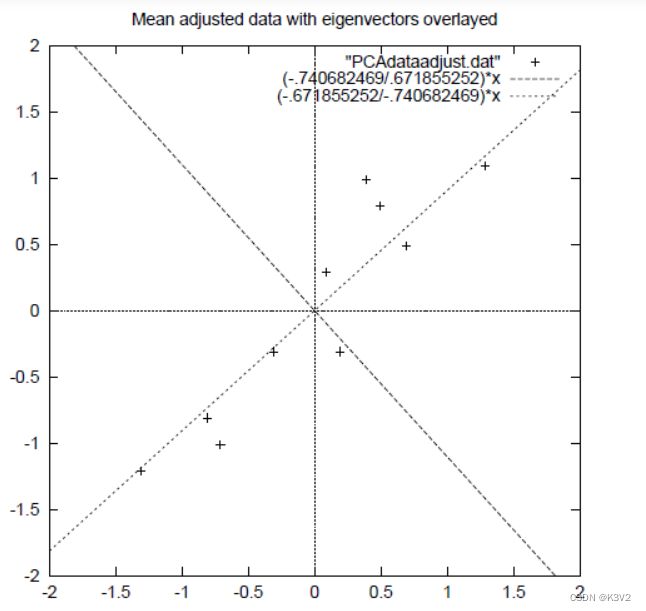
正号表示预处理后的样本点,斜着的两条线就分别是正交的特征向量(由于协方差矩阵是对称的,因此其特征向量正交),最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。
这就是经过PCA处理后的样本数据,水平轴(上面举例为LS特征)基本上可以代表全部样本点。整个过程看起来就像将坐标系做了旋转,当然二维可以图形化表示,高维就不行了。上面的如果k=1,那么只会留下这里的水平轴,轴上是所有点在该轴的投影。这样PCA的过程基本结束。在第一步减均值之后,其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度(0到100),一个是汽车的座位数(2到6),显然第二个的方差比第一个小。因此,如果样本特征中存在这种情况,那么在第一步之后,求每个特征的标准差,然后对每个样例在该特征下的数据除以标准差。
PCA算法实现步骤
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值排序
保留前N个最大的特征值对应的特征向量
将数据转换到上面得到的N个特征向量构建的新空间中说到这里,我们来用代码实现一下,这里我们需要用到python强大的Numpy库,用来直接求解矩阵的特征向量和特征值。奇妙!
在得到我们需要的特征向量后,需要对数据进行映射,计算方法为: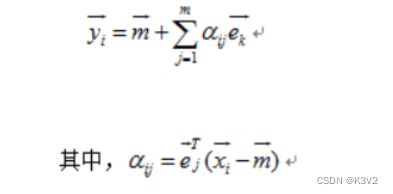
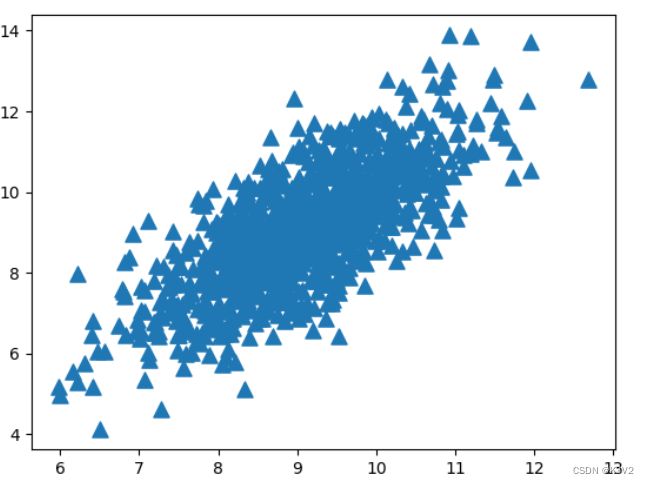
向量e为通过点m处的某条直线的方向向量,α为某个样本点至点m处的距离。先来看一下源数据集的数据分布情况:
我们现在要对这个二维数据集降维。
为什么要降维:
在许多领域的研究与应用中,往往需要对反映事物的多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息,但也在一定程度上增加了数据采集的工作量,更重要的是在多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。盲目减少指标会损失很多信息,容易产生错误的结论。
降维是对数据高维度特征的一种预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为了应用非常广泛的数据预处理方法。
对二维数据集降维的具体代码如下:
准备工作
下载pca_algo.tgz到指定目录下(https://pan.baidu.com/s/1m4oOBrgtrCfUaVXCeEO9kQ
提取码:k3v2),然后再再jupyter上依次选择点击上方的File->Open->Upload,上传刚才下载的数据集压缩包,再使用如下命令解压:
!tar -zxvf pca_algo.tgz解压测试文件:
结果如下:
pca_algo/ pca_algo/testSet.txt
from numpy import *
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:加载数据集
parameters:
fileName -文件名
delim -分隔符
return:
mat(datArr) -数据矩阵
"""
def loadDataSet(fileName, delim = '\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()] #对读入数据以\t分隔存储到列表中
datArr = [list(map(float,line)) for line in stringArr] #使用两个list来构建矩阵
return mat(datArr)
"""
函数说明:PCA算法实现
parameters:
dataMat -用于进行PCA操作的数据集
topNfeat -应用的N个特征
return:
lowDataMat -将维后的数据集
reconMat -重构的数据集(用于调试)
"""
def pca(dataMat, topNfeat = 9999999):
meanVals = mean(dataMat, axis = 0) #计算数据平均值
meanRemoved = dataMat - meanVals #去中心化
covMat = cov(meanRemoved, rowvar = 0 ) #计算协方差
#补充下面代码,按照注释的思路完成PCA的计算
eigenvalues,eigenvectors=np.linalg.eig(covMat) #计算协方差矩阵的特征值和特征向量
eigenvaluessort_index=np.argsort(eigenvalues)
#print(eigenvalues,eigenvectors, eigenvaluessort_index)#对特征值从小到大排序,并提取对应的index
topk_eigenvectors=eigenvectors[:,eigenvaluessort_index[:-topNfeat-1:-1]]#对特征排序结果逆序,并保留topNfeat的index,根据特征值排序结果得到topNfeat个最大的特征向量
#print(topk_eigenvectors)
lowDataMat=np.dot(meanRemoved,topk_eigenvectors) #数据降维
#print(lowDataMat)
print(meanRemoved)
print(topk_eigenvectors)
lowDataMat=np.dot(lowDataMat,topk_eigenvectors.T)
reconMat=lowDataMat+meanVals #降维后的数据重构(对比上面的计算公式,注意前面有去中心化操作,需要恢复)
return lowDataMat, reconMat
"""
函数说明:绘制数据集
parameters:
dataMat -原始数据集
reconMat -重构数据集
return:
None
"""
def drawDataSet(dataMat, reconMat):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0].flatten().A[0], dataMat[:,1].flatten().A[0], marker='^',s=90)
ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o',s=50,c='red')
plt.show()
if __name__ =='__main__':
dataMat = loadDataSet('pca_algo/testSet.txt')
lowDMat, reconMat = pca(dataMat,1)
print("降维后的矩阵形状:\n",shape(lowDMat))
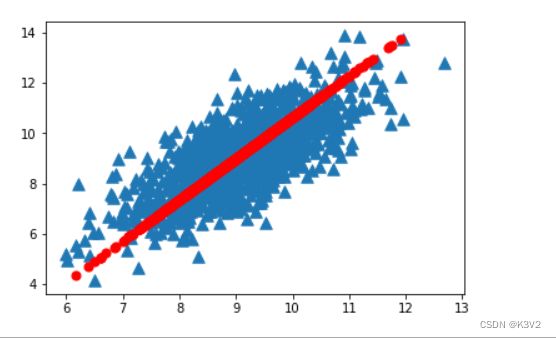
drawDataSet(dataMat, reconMat)结果如下:
[[ 1.17124956 2.22599482] [ 1.05840256 2.71499082] [ 0.12629956 -0.19105918] ..., [ 0.79098556 0.10539082] [ 0.05064356 0.03821282] [ 1.27096256 -0.55239818]] [[-0.52045195] [-0.85389096]] 降维后的矩阵形状: (1000, 2)
运行后,我们可以看到红色的数据即为我们降维后的数据,且降维后的矩阵为一维矩阵。图中蓝色点为原始数据集,红色点为我们处理后得到的第一主成分。
使用sklearn实现PCA算法
直接调用PCA库函数即可
如:
pca = PCA(n_components=1) #此处可修改想要降维的维度
pca.fit(数据集).transform(数据集)
具体使用方法自行csdn;