SpaceClaim脚本建模初试（一）

   SpaceClaim2019也提供了脚本建模的选项，通过合理规划可以非常方便的创建系列零件，方便快速建模，节省时间，就此方面做个学习记录，并分享出来，与大家交流共同进步，本人python是自学的，可能某些代码规范并不太清楚，请勿吐槽。

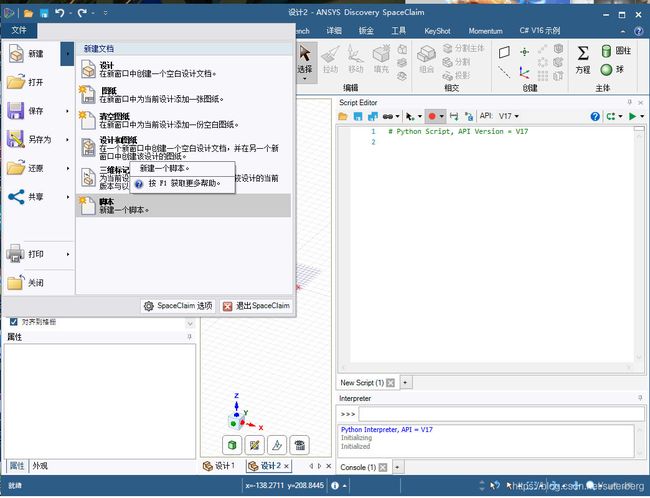
    这次是基于Ansys 19 R1自带的SpaceClaim版本，通过如图方式新建脚本，API版本为V17，具体建模方式就不做介绍了，大家可以自行学习非常简单。

              

具体API方式可以查询帮助文档，里边非常详细的解释。

    现在正式开始学习，首先先建立一个poi类，方便点的计算具体代码如下

class poi():
    def __init__(self, x, y):
        self.x = x
        self.y = y
    def addx(self, inx):#x坐标增加
        self.x = self.x + inx
        return self

    def addy(self, inx):#y坐标增加
        self.y = self.y + inx
        return self

    def adds(self, inx):#x，y坐标增加
        self.x = self.x + inx.x
        self.y = self.y + inx.y
        return self
     
    def rettup(self):
        return (self.x,self.y)

    def __add__(self, other):# +号定义
        x = self.x + other.x
        y = self.y + other.y
        return poi(x, y)

    def __str__(self):
        return 'x:%7d ,y:%7d' % (self.x, self.y)

接着创建关于草绘平面相关函数，为了以后封装方便，将原函数拆分为几个函数

def sketch(p,x,y):#创建草绘指令
    Pl=plane(p,x,y)
    ViewHelper.SetSketchPlane(Pl)

def plane(p,x,y):#创建平面
    pl=Plane.Create(frame(p,x,y))
    return pl
def frame(p,x,y):#创建坐标框架
    fs=Frame.Create(poitcs(p),direct(x),direct(y))
    return fs

def poitcs(po):#将点转换为需要的点参数
    return Point.Create(MM(po.x), MM(po.y), MM(po.z))
def direct(po):#创建方向数据
    return Direction.Create(po[0],po[1],po[2])



p=poi3(0,0，0)
sketch(p,(1,0,0),(0,1,0))#在（0，0，0）点，以x轴为X方向，y轴为Y方向创建草绘，可以根据需要调整方向。

忘了创建三维点类了

class poi3():
    def __init__(self, x, y,z):
        self.x = x
        self.y = y
        self.z = z
    def addx(self, inx):
        self.x = self.x + inx
        return self

    def addy(self, inx):
        self.y = self.y + inx
        return self
    
    def addz(self, inx):
        self.z = self.z + inx
        return self

    def adds(self, inx):
        self.x = self.x + inx.x
        self.y = self.y + inx.y
        self.z = self.z + inx.z
        return self
    def addtup(self, inx):
        self.x = self.x + inx[0]
        self.y = self.y + inx[1]
        self.z = self.z + inx[2]
        return self
    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        z=self.z+ other.z
        return poi3(x, y,z)
    def rettup(self):
        return (self.x,self.y,self.z)

    def __str__(self):
        return 'x:%7d ,y:%7d' % (self.x, self.y)
    

接着点击执行就可以看到具体效果了，记得先切回三维模式再尝试。暂时就到这了，其他有时间再发。