【数学建模】机器学习预测算法(KNN、随机森林、网格搜索对决策树、支持向量机)(Python代码实现)【2021华为杯】
目录
1 题目
2 数据集介绍及建模目标
3 问题
4 简化描述
5 Python代码实现
1 题目
乳腺癌是目前世界上最常见,致死率较高的癌症之一。乳腺癌的发展与雌激素受体密切相关,有研究发现,雌激素受体α亚型(Estrogen receptors alpha, ERα)在不超过10%的正常乳腺上皮细胞中表达,但大约在50%-80%的乳腺肿瘤细胞中表达;而对ERα基因缺失小鼠的实验结果表明,ERα确实在乳腺发育过程中扮演了十分重要的角色。目前,抗激素治疗常用于ERα表达的乳腺癌患者,其通过调节雌激素受体活性来控制体内雌激素水平。因此,ERα被认为是治疗乳腺癌的重要靶标,能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。比如,临床治疗乳腺癌的经典药物他莫昔芬和雷诺昔芬就是ERα拮抗剂。
目前,在药物研发中,为了节约时间和成本,通常采用建立化合物活性预测模型的方法来筛选潜在活性化合物。具体做法是:针对与疾病相关的某个靶标(此处为ERα),收集一系列作用于该靶标的化合物及其生物活性数据,然后以一系列分子结构描述符作为自变量,化合物的生物活性值作为因变量,构建化合物的定量结构-活性关系(Quantitative Structure-Activity Relationship, QSAR)模型,然后使用该模型预测具有更好生物活性的新化合物分子,或者指导已有活性化合物的结构优化。
一个化合物想要成为候选药物,除了需要具备良好的生物活性(此处指抗乳腺癌活性)外,还需要在人体内具备良好的药代动力学性质和安全性,合称为ADMET(Absorption吸收、Distribution分布、Metabolism代谢、Excretion排泄、Toxicity毒性)性质。其中,ADME主要指化合物的药代动力学性质,描述了化合物在生物体内的浓度随时间变化的规律,T主要指化合物可能在人体内产生的毒副作用。一个化合物的活性再好,如果其ADMET性质不佳,比如很难被人体吸收,或者体内代谢速度太快,或者具有某种毒性,那么其仍然难以成为药物,因而还需要进行ADMET性质优化。为了方便建模,本试题仅考虑化合物的5种ADMET性质,分别是:1)小肠上皮细胞渗透性(Caco-2),可度量化合物被人体吸收的能力;2)细胞色素P450酶(Cytochrome P450, CYP)3A4亚型(CYP3A4),这是人体内的主要代谢酶,可度量化合物的代谢稳定性;3)化合物心脏安全性评价(human Ether-a-go-go Related Gene, hERG),可度量化合物的心脏毒性;4)人体口服生物利用度(Human Oral Bioavailability, HOB),可度量药物进入人体后被吸收进入人体血液循环的药量比例;5)微核试验(Micronucleus,MN),是检测化合物是否具有遗传毒性的一种方法。
2 数据集介绍及建模目标
本试题针对乳腺癌治疗靶标ERα,首先提供了1974个化合物对ERα的生物活性数据。这些数据包含在文件“ERα_activity.xlsx”的training表(训练集)中。training表包含3列,第一列提供了1974个化合物的结构式,用一维线性表达式SMILES(Simplified Molecular Input Line Entry System)表示;第二列是化合物对ERα的生物活性值(用IC50表示,为实验测定值,单位是nM,值越小代表生物活性越大,对抑制ERα活性越有效);第三列是将第二列IC50值转化而得的pIC50(即IC50值的负对数,该值通常与生物活性具有正相关性,即pIC50值越大表明生物活性越高;实际QSAR建模中,一般采用pIC50来表示生物活性值)。该文件另有一个test表(测试集),里面提供有50个化合物的SMILES式。
其次,在文件“Molecular_Descriptor.xlsx”的training表(训练集)中,给出了上述1974个化合物的729个分子描述符信息(即自变量)。其中第一列也是化合物的SMILES式(编号顺序与上表一样),其后共有729列,每列代表化合物的一个分子描述符(即一个自变量)。化合物的分子描述符是一系列用于描述化合物的结构和性质特征的参数,包括物理化学性质(如分子量,LogP等),拓扑结构特征(如氢键供体数量,氢键受体数量等),等等。关于每个分子描述符的具体含义,请参见文件“分子描述符含义解释.xlsx”。同样地,该文件也有一个test表,里面给出了上述50个测试集化合物的729个分子描述符。
最后,在关注化合物生物活性的同时,还需要考虑其ADMET性质。因此,在文件“ADMET.xlsx”的training表(训练集)中,提供了上述1974个化合物的5种ADMET性质的数据。其中第一列也是表示化合物结构的SMILES式(编号顺序与前面一样),其后5列分别对应每个化合物的ADMET性质,采用二分类法提供相应的取值。Caco-2:‘1’代表该化合物的小肠上皮细胞渗透性较好,‘0’代表该化合物的小肠上皮细胞渗透性较差;CYP3A4:‘1’代表该化合物能够被CYP3A4代谢,‘0’代表该化合物不能被CYP3A4代谢;hERG:‘1’代表该化合物具有心脏毒性,‘0’代表该化合物不具有心脏毒性;HOB:‘1’代表该化合物的口服生物利用度较好,‘0’代表该化合物的口服生物利用度较差;MN:‘1’代表该化合物具有遗传毒性,‘0’代表该化合物不具有遗传毒性。同样地,该文件也有一个test表,里面提供有上述50个化合物的SMILES式(编号顺序同上)。
建模目标:根据提供的ERα拮抗剂信息(1974个化合物样本,每个样本都有729个分子描述符变量,1个生物活性数据,5个ADMET性质数据),构建化合物生物活性的定量预测模型和ADMET性质的分类预测模型,从而为同时优化ERα拮抗剂的生物活性和ADMET性质提供预测服务。
3 问题
问题1:参考这篇文章:华为杯学习——特征选择(Python代码实现)
问题2. 请结合问题1,选择不超过20个分子描述符变量,构建化合物对ERα生物活性的定量预测模型,请叙述建模过程。然后使用构建的预测模型,对文件“ERα_activity.xlsx”的test表中的50个化合物进行IC50值和对应的pIC50值预测,并将结果分别填入“ERα_activity.xlsx”的test表中的IC50_nM列及对应的pIC50列。
4 简化描述
选择不超过20个特征,构建IC50值和pIC50值的定量预测模型,并计算测试样本的IC50值和pIC50值。
方案: 机器学习预测算法构建
5 Python代码实现
'''导入相关库'''
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split #拆分数据集
from sklearn.ensemble import RandomForestRegressor #随机森林
from sklearn.metrics import r2_score #评估模型
from sklearn.decomposition import PCA #主要成分分析
from sklearn.preprocessing import StandardScaler#标准化数据
from sklearn.svm import SVR #支持向量机,定量预测模型1
from sklearn.tree import DecisionTreeRegressor #决策树
from sklearn.model_selection import GridSearchCV # 网格搜索,定量预测模型2
from sklearn.neighbors import KNeighborsRegressor #KNN,定量预测模型3
from sklearn.model_selection import GridSearchCV
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文字体设置-黑体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
sns.set(font='SimHei',font_scale=1.5) # 解决Seaborn中文显示问题并调整字体大小
'''读取数据'''
data=pd.read_excel('ERα_activity.xlsx')
data2=pd.read_excel('Molecular_Descriptor.xlsx')
#====两个数据集做列合并==========
data_ER_X = data.drop(["SMILES"], axis=1) # 删除重复特征
data3 = pd.concat([data,data2], axis=1) # 列合并
#res=data3
#res.to_excel('合并数据.xlsx')
#data3=pd.read_excel('合并数据.xlsx')
'''数据处理'''
#===(1)提取特征和目标:============
X = data3.drop(['SMILES','IC50_nM','pIC50'],axis=1) # 特征
y = data3.loc[:, ['IC50_nM','pIC50']] # 目标
#===(2)拆分数据集==============
X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
#====(3)分别提取两个特征的训练和测试数据:===========
y_IC50_train = y_train.loc[:,"IC50_nM"]
y_pIC50_train = y_train.loc[:,"pIC50"]
y_IC50_test = y_test.loc[:,"IC50_nM"]
y_pIC50_test = y_test.loc[:,"pIC50"]
'''构建模型'''
#使用随机森林构建先预测IC50_nM
#使用随机森林的方法构建模型
rf_model = RandomForestRegressor(n_estimators=100)
rf_model.fit(X_train,y_pIC50_train) # 预测IC50_nM的模型训练
# 评估模型
predict = rf_model.predict(X_train)
print("训练准确度为::",r2_score(y_pIC50_train,predict))
predict = rf_model.predict(X_test)
print("测试准确度为:",r2_score(y_pIC50_test,predict))
'''获取重要性排名:'''
features = X.columns # 读取列命
feature_importances = rf_model.feature_importances_ # 获取每个特征重要性
features_df = pd.DataFrame({'特征':features,'重要性':feature_importances}) #
features_df.sort_values('重要性',inplace=True,ascending=False) # 排序
#print(features_df)
#获取重要性最高的前20名:
print(features_df[:20])
'''选择不超过20个特征'''
# 读取最重要的20个特征
X_train = X_train.loc[:,features_df[:20]["特征"]]
X_test = X_test.loc[:,features_df[:20]["特征"]]
print(X_train.head())
'''选择不超过20个分子描述符变量,那么主成成分分析:'''
'''(1)对20个特征进行pca主成分分析'''
pca = PCA(n_components=20)
pca.fit(X_train)
#查看各个特征的方差
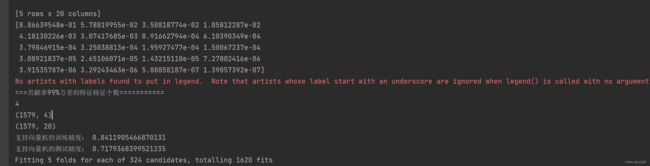
print(pca.explained_variance_ratio_)
# 可视化
plt.xlabel("Demensions")
plt.ylabel("explained_variance_ratio")
plt.plot([i for i in range(X_train.shape[1])],[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.legend()
plt.show()
'''(2)选取贡献率99%方差的特征'''
pca = PCA(0.99)
pca.fit(X_train)
print('===贡献率99%方差的特征特征个数===========')
print(pca.n_components_) # 特征个数
'''(3)筛选到九个特征后标准化:'''
X_train_pca = pca.transform(X_train) # 筛选到九个特征后标准化
X_test_pca = pca.transform(X_test)
print(X_train_pca.shape)
'''构建定量预测模型'''
# (1)标准化数据
std = StandardScaler()
std.fit(X_train)
X_train_std = std.transform(X_train)
X_test_std = std.transform(X_test)
print(X_train_std.shape) # 查看大小
'''建立模型并评估:'''
#==(1)建立SVM模型并对模型的R2值进行评估 rbf内核=======
svr = SVR(tol=1e-5, kernel='rbf',C=1e1)
svr.fit(X_train_std,y_pIC50_train)
# 判断是否过拟合
print("支持向量机的训练精度:",svr.score(X_train_std, y_pIC50_train))
print("支持向量机的测试精度:",svr.score(X_test_std, y_pIC50_test))
#====(2)使用网格搜索对决策树进行寻优并评估:==========
# 建立决策树模型并对模型的R2值进行评估
param_grid = [
{
"criterion": ["squared_error","absolute_error","mae"],
"max_depth": [10,20,30,40,50,100],
'min_samples_leaf': [1,2,3,5,7,10],
'min_impurity_decrease': [0.1,0.2,0.3]
}
]
dtr = DecisionTreeRegressor()
dtr_grid = GridSearchCV(dtr, param_grid, n_jobs=-1, verbose=1)
dtr_grid.fit(X_train,y_pIC50_train)
print("最优超参数为:",dtr_grid.best_params_)
print("训练精度:",dtr_grid.best_estimator_.score(X_train, y_pIC50_train))
print("测试精度:",dtr_grid.best_estimator_.score(X_test, y_pIC50_test))
#====(3)KNN模型===============
param_grid = [
{
"weights": ["uniform"],
"n_neighbors": [i for i in range(1, 11)]
},
{
"weights": ["distance"],
"n_neighbors": [i for i in range(1, 11)],
"p": [i for i in range(1,6)]
}
]
knn = KNeighborsRegressor()
grid_search = GridSearchCV(knn, param_grid, n_jobs=-1, verbose=1)
grid_search.fit(X_train_std, y_pIC50_train)
print("最优超参数为:",grid_search.best_params_)
print("KNN训练精度:",grid_search.best_estimator_.score(X_train_std, y_pIC50_train))
print("KNN测试精度:",grid_search.best_estimator_.score(X_test_std, y_pIC50_test))
#======(4)随机森林==============
param_grid_rf = [
{
"max_depth": [30,40,50],
'min_samples_leaf': [1,2,3],
'n_estimators': [300,400,500],
}
]
rf_model = RandomForestRegressor()
rf_grid = GridSearchCV(rf_model, param_grid_rf, n_jobs=-1, verbose=1)
rf_grid.fit(X_train,y_pIC50_train)
print("最优超参数为:",rf_grid.best_params_)
print("RandomForest训练精度",rf_grid.best_estimator_.score(X_train,y_pIC50_train))
print("RandomForest测试精度:",rf_grid.best_estimator_.score(X_test,y_pIC50_test))
'''预测并填入表格'''
data4=pd.read_excel('Molecular_Descriptor.xlsx',sheet_name='test') # 测试集
print(data4)
#data4.to_excel('data4.xlsx')
#再读取另一个活性表格测试:
data5=pd.read_excel("./ERα_activity.xlsx",sheet_name='test')
print(data5)
#data5.to_excel('data5.xlsx')
'''读取前二十个特征:'''
#测试集的特征选择
X_final = data4.drop(['SMILES'],axis=1) # 删除描述
X_final = X_final.loc[:,features_df[:20]["特征"]] # 前二十个特征
print(X_final.head())
'''使用模型预测并保存:'''
# 使用训练好的随机森林模型进行预测,也可以用其他几个效果不错的
y_final_pIC50 = rf_grid.predict(X_final) # 预测数据
data5.loc[:,["pIC50"]] = y_final_pIC50
y_final_IC50 = np.power(10,-y_final_pIC50)/(10**-9) #负对数
data5.loc[:,["IC50_nM"]] = y_final_IC50
data5.to_excel("ERα_activity_predict.xlsx",index=False)结果: