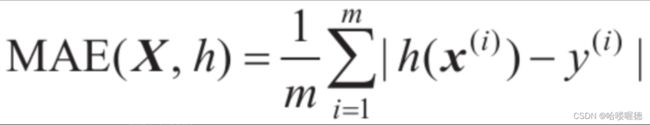机器学习实战——端到端的机器学习项目
驱动任务:根据加州住房价格的数据集建立加州的房价模型
数据集下载地址:https://pan.baidu.com/s/1it08eJ7a1ZGTTc7mHBZVzw?pwd=9n13
2.2 设计系统
典型的有监督学习任务,已经给出了标记的训练示例(每个实例都有预期的产出,也就是该区域的房价中位数)。并且也是一个典型的回归任务,因为哟啊对某个值进行预测。
选择性能指标
回归问题的典型性能指标是均方根误差RMSE:
- m为数据集中的实例数
- x(i)是数据集中第i个实例的所有特征值(不包括标签)的向量,y(i)是其标签(该实例预期输出值)
- X是一个矩阵,其中包含数据集中所有实例的所有特征值(不包括标签)。每个实例只有一行,第i行等于x(i)的转置,记为(x(i))
- h是系统的预测函数,也称为假设y=h(x(i))
尽管RMSE通常是回归任务的首选性能指标,但是在有许多异常区域的情况下,可以考虑使用平均绝对误差MAE
2.3 读取数据和基本分析
import pandas as pd
import matplotlib.pyplot as plt
housing = pd.read_csv('D:\Coding\IDE\Python\workspace\MLInAction\ChapterOne\dataset\housing.csv')
print(housing.head()) # 显示数据前五行
print(housing.info()) # 获得数据集的简单描述
print(housing.describe()) # 获得数据集中数值型数据的(数量、均值、标准差、最小值、上四分位、中位、下四分位、最大值)
housing.hist(bins=50, figsize=(20,15)) # 绘制每个数值属性的直方图
plt.show()
划分数据集
将数据集划分为训练集和测试集,只需要随机选择一些示例,通常是数据集的20%(如果数据很大,比例会小一些)
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data)*test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
但是使用上述的方法在下一次运行,会产生一个不同的数据集,这样下去会看到整个完整的数据集,这是需要避免的,因此采用以下这种方式产生一个稳定的训练测试分割:使用标识符决定是否进入测试集(例如哈希值),如果这个哈希值小于等于最大哈希值的20%,则将该实例放入测试集。这样可以确保测试集在多个运行里都是一致的,新实例的20%也将被放入新的测试集,而之前训练集中的实例也不会被放入新测试集。下面采用行索引作为标识符序列:
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio*2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_:test_set_check(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
Scikit-Learn提供了一些函数,可以通过多种方式将数据集分成多个子集,最简单的是train_test_split。与前面实现的函数类似,增加了几个额外特征:random_state参数设定随机生成器种子。
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
连续数值属性分类
以收入中位数为例,确保测试集能够代表数据集中各种不同类型的收入,需要创建一个收入类别的属性:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
housing = pd.read_csv('D:\workspace\MLInAction\ChapterOne\dataset\housing.csv')
housing['income_cat'] = pd.cut(housing['median_income'],
bins=[0., 1.5, 3.0, 4.5, 6.,np.inf],
labels=[1, 2, 3, 4, 5])
housing['income_cat'].hist()
plt.show()
然后根据分类的值,对收入类别进行分层采样分割训练集和测试集:
from sklearn.model_selection import StratifiedShuffleSplit
split_model = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split_model.split(housing, housing['income_cat']):
start_train_set = housing.loc[train_index]
start_test_set = housing.loc[test_index]
2.4 数据可视化
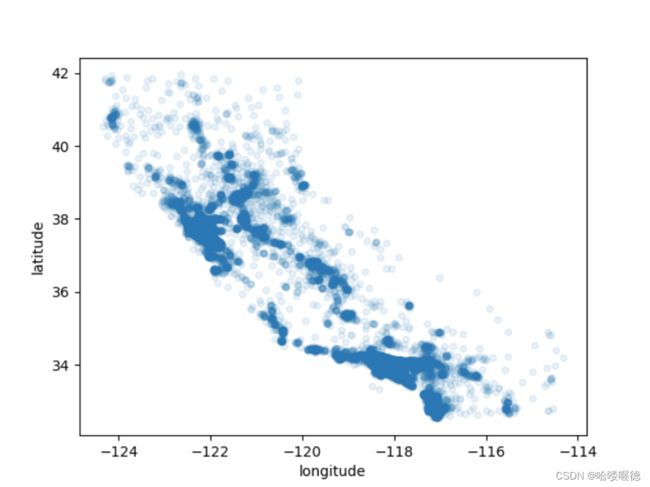
由于存在地理位置信息(经度和纬度),因此可建立以恶搞区域分布图便于可视化数据:
housing = start_train_set.copy()
housing.plot(kind='scatter', x='longitude', y='latitude', alpha=0.1)
plt.show()
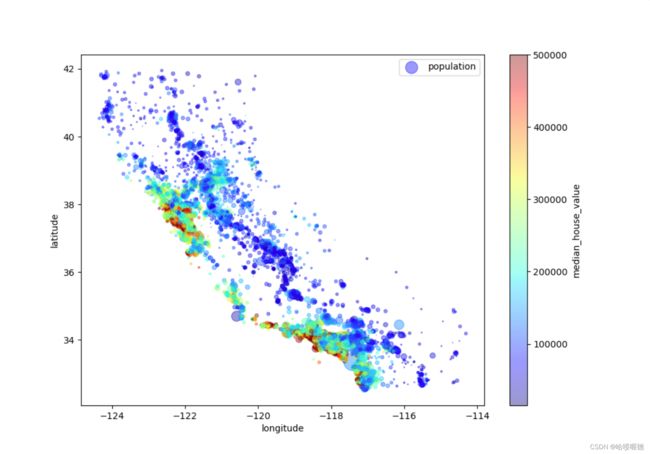
然后使用房价进行数据可视化,其中:
- 每个圆的半径大小代表区域的人口数量(选项s)
- 颜色代表价格(选项c)
- 使用名叫jet的预定义颜色表(选项cmap)
housing.plot(kind='scatter', x='longitude', y='latitude', alpha=0.4,
s=housing['population']/100, label='population', figsize=(10,7),
c='median_house_value', cmap=plt.get_cmap('jet'),colorbar=True)
plt.legend() # 添加图例
plt.show()
寻找相关性
由于数据集不大,可以使用corr()方法计算每堆属性之间的标准相关系数(也称为皮尔逊r)
corr_matrix = housing.corr()
print(corr_matrix['median_house_value'].sort_values(ascending=False))
2.5 数据准备
数据清洗
大部分机器学习算法无法在缺失的特征上工作,所以需要创建一些函数补充它,一般有三种选择:
- 放弃这些相应的区域
- 放弃整个属性
- 将缺失值设置为某个值(0、平均数、中位数等)
我们上面提到的数据集中的total_bedrooms属性有部分缺失,所以可以这样处理:
housing.dropna(subset=['total_bedrooms'])
housing.drop('total_bedrooms', axis=1)
housing['total_bedrooms'].fillna(housing['total_bedrooms'].median, inplace=True)
Scikit-Learn提供了一个非常容易上手的类来处理缺失值:SimpleImputer。由于中位数值智能在数值数据上计算,所以需要创建一个没有文本属性的ocean_proximity的数据副本
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='median') # 使用中位数填充
housing_num = housing.drop('ocean_proximity', axis=1)
imputer.fit(housing_num) # 计算中位数
print(imputer.statistics_)
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns, index=housing_num.index) # 放回dataframe
处理文本数据和分类属性
大多数机器学习算法更喜欢使用数字,所以我们经常将文本属性处理为数字,可以使用Scikit-Learn的OrdinalEncoder类。
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat = housing[['ocean_proximity']]
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
print(ordinal_encoder.categories_)
然后可以使用categories_属性获取到类别列表,列表包含每个类别属性的一维数组。这种表征方式产生的一个问题是机器学习算法会认为两个相近的值比两个离得较远的值更为相似一些。在某些状况下是对的,但是对于ocean_proximity并非如此。这时候可以使用OneHot编码:即一个属性为1时其他属性为0。Scikit-Learn提供了OneHotEncoder编码器。
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat = housing[['ocean_proximity']]
housing_cat_1hot = cat_encoder.fit_transform(housing_cat) # 得到SciPy稀疏矩阵
print(housing_cat_1hot.toarray()) # 转化为NumPy矩阵
自定义转换器
输入Scikit-Learn提供了很多有用的转换器,但是仍然需要为一些诸如自定义清理擦做或组合特定属性的任务编写自己的转换器。Scikit-Learn依赖于鸭子类型的编译,因此只需要创建一个类,然后应用fit()、transform()、fit_transform()方法。
可以通过添加TransformerMixin作为基类得到最后一种方法,同时添加BaseEstimator作为基类(并在构造函数中避免args和kargs)还可以得到两种调整超参数的方法(get_params()、set_params())。下面以卧室/房间数量的组合属性自定义一个转换器类:
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room=True): # 没有*args *kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self
def transform(self, X):
rooms_per_household = X[:,rooms_ix] / X[:,households_ix]
population_per_household = X[:,population_ix] / X[:,households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:,bedrooms_ix] / X[:,rooms_ix]
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.value)
特征放缩
最重要也是最需要应用到数据上的转换就是特征缩放。如果输入的数值属性具有非常大的差异,往往会导致机器学习算法的性能不佳。同比例方所的所有属性两种常用方法为最小最大化和标准化。
- 最大最小化:又称归一化,将值重新缩放到最终范围归于01之间。对此Scikit-Learn提供了名为MinMaxScaler的转换器,如果希望范围不是01可以调整超参数feature_range进行更改。
- 标准化:首先减去平均值,然后除以方差,从而使得结果的分布具备单位方差。对此Scikit-Learn提供了名为StandadScaler的转换器
跟所有转换一样,缩放器仅用来拟合训练集而不是完整的数据集。
转换流水线
许多数据转换的步骤需要以正确的顺序进行。Scikit-Learn提供了Pipeline流水线来支持这样的转换。例如:
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([('imputer', SimpleImputer(strategy='median')),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler())])
当调用流水线的fit()方法时,会在所有的转换器上按照顺序依次调用fit_transform(),将一个调用的输出作为参数传递给下一个调用方法,知道传递到最终的估算器,则只会调用fit()方法。流水线的方法和最终估算器的方法相同。
到目前为止我们分别处理了数值列和类别列。拥有一个能够处理所有列的转换器更方便,将适当的转换应用于每个列。
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ['ocean_proximity']
full_pipeline = ColumnTransformer([('num', num_pipeline, num_attribs),
('cat', OneHotEncoder(), cat_attribs)])
ColumnTransformer的构造函数需要一个元组列表其中每个元组包含一个名字、一个转换器以及这个转换器能够应用的列名或索引的列表。在此示例中,指定数值列尔使用num_pipeline转换,类别类使用OneHot编码转换,最终沿第二个轴合并输出(转换器必须返回相同数量的行)
2.6 选择和训练模型
训练模型
训练一个线性回归模型,并用前5个数据预测:
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print(lin_reg.predict(some_data_prepared))
print(list(some_labels))
从结果显示预测不是很准确,可以使用Scikit-Learn的mean_squared_error()来测量整个训练集上回归模型的RMSE:
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
line_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(line_mse)
print(lin_rmse)
如果前面的步骤正确,这里得到的预测误差在68628左右。说明模型对训练数据欠拟合。如果想要修正欠拟合,可以通过选择更强大的模型,或为算法训练提供更好的特征,又或者减少对模型的限制等方法。这里我们尝试一个更复杂的模型DecisionTreeRegressor(决策树)
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
print(tree_rmse)
这里不出意外会得到0的结果,这说明该模型对数据严重过拟合了。需要使用测试集进行确认。
模型评估
评估决策树模型的一种方法是K折交叉验证:这里将训练集分割为10个不同的子集,每个子集称为一个折叠,然后对决策树模型进行10次训练和评估——每次挑选1个进行评估,使用另外9个进行训练。产生的结果是一个包含10次评估分数的数组:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring='neg_mean_squared_error', cv=10)
tree_rmse_scores = np.sqrt(-scores)
print(tree_rmse_scores)
print(tree_rmse_scores.mean())
print(tree_rmse_scores.std())
交叉验证功能更倾向于使用效用函数(越大越好),而不是成本函数(越小越好)。所以计算分数的函数实际是负的MSE函数,因此这里需要加负号。最终输出的分数结果显示还不如线性回归模型。
最后尝试使用RandomForestRegressor(随机森林),其工作原理是通过随机子集进行多个决策树的训练,然后对预测取平均。在多个模型的基础上建立模型称为集成学习。
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forset_mse = mean_squared_error(housing_labels, housing_predictions)
forset_rmse = np.sqrt(forset_mse)
print(forset_rmse)
scores = cross_val_score(forest_reg, housing_prepared, housing_labels, scoring='neg_mean_squared_error', cv=10)
forset_rmse_scores = np.sqrt(-scores)
print(forset_rmse_scores)
print(forset_rmse_scores.mean())
print(forset_rmse_scores.std())
2.7 微调模型
已经有了一个有效模型的候选列表,现在需要微调。一种微调的方法是手动调整超参数,直到找到一组很好的超参数组合。还可以使用Scikit-Learn的GridSearchCV,只需要告诉它要进行实验的参数是什么以及需要尝试的值,它将会使用交叉验证来评估超参数的所有可能组合。下面代码搜索随机森林的超参数值的最佳组合:
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
param_grid = [{'n_estimators':[3,10,30], 'max_features':[2,4,6,8]},
{'bootstrap':[False], 'n_estimators':[3,10], 'max_features':[2,3,4]}]
forset_reg = RandomForestRegressor()
grid_search = GridSearchCV(forset_reg, param_grid, cv=5, scoring='neg_mean_squared_error', return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
print(grid_search.best_params_) # 输出最佳的参数组合
print(grid_search.best_estimator_) # 输出最好的估算器
# 输出每种组合的评估分数
cvres = grid_search.cv_results_
for mean_scores, params in zip(cvres['mean_test_score'], cvres['params']):
print(np.sqrt(-mean_scores), params)
当超参数不知道该赋什么值时,一个简单的方法是尝试10的连续幂次方。上方代码示例中的参数网格表示,首先评估第一个字典里的n_estimators和max_features的3*4=12中超参数组合。第二个字典里有6种组合。总共达到18种组合,每个模型训练5次(5折交叉验证)。
如果探索的组合数量较少,那么网格搜索是一种不错的方法,但是当超参数的搜索范围较大时,通常会优先选择使用RandomizedSearchCV。在每次迭代中为每个超参数选择一个随机值,然后对一定数量的随机组合进行评估。通过简单地设置迭代次数,可以更好的控制要分配给超参数搜索的计算预算。
通过测试集评估系统
从测试集获取预测器和标签,运行full_pipeline来转换数据,然后再测试集上评估最终模型。
final_model = grid_search.best_estimator_
X_test = start_test_set.drop('median_house_value', axis=1)
y_test = start_test_set['median_house_value'].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_prediction = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_prediction)
final_rmse = np.sqrt(final_mse)
print(final_rmse)