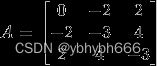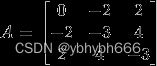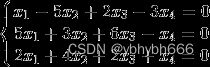python在高等数学和线性代数中的应用
python在高等数学和线性代数中的应用
一.sympy工具库介绍
首先我们可以通过help(‘sympy’)来看到他有数十个板块
abc：符号变量模块；
calculus：积分相关方法；
core：基本的加、乘、指数运算等；
discrete：离散数学；
functions：基本的函数和特殊函数；
galgebra：几何代数；
geometry：几何实体；
integrals：符号积分；
interactive：交互会话（如IPython）
logic：布尔代数和定理证明；
matrices：线性代数和矩阵；
ntheory：数论函数；
physics：物理学；
plotting：用Pyglet进行二维和三维的画图。
polys：多项式代数和因式分解；
printing：漂亮的打印和代码生成；
series：级数；
simplify：化简符号表达式；
solvers：方程求解；
stats：统计学。
1.1 符号运算基础知识
使用Python的SymPy库进行符号计算，首先要建立符号变量以及符号表达式。
符号变量是构成符号表达式的基本元素，可以通过库中的symbols()函数创建。例如：
from sympy import *
x=symbols('x')
y,z=symbols('y z')
可以看到，如果想一次性构建多个符号，记得在中间加空格，符号变量的名称和值不一定相同
还有一种方法是用m0:3传入符号函数
m0,m1,m2,m3=symbols('m0:4')
在符号对象中，用evalf()或者n（）方法来获得任何对象的浮点近似值，默认的小数点精度是15位，可以通过调参来得到自己想要的精度
举例：符号创建、类型转换、以及subs()方法代入实例
x,y,z=symbols('x y z')
m0,m1,m2,m3=symbols('m0:4')
x=sin(1)
print('x=',x)
print('x=',x.evalf())
print('x=',x.n(16))#小数点后16位
print(pi,pi.evalf(3))#这里不能使用n函数
expr1=y*sin(y**2)#创建第一个符号表达式
expr2=y**2+sin(y)*cos(y)+sin(z)#创建第二个符号表达式
print('expr1=',expr1)
print('当y=5时，expr1=',expr1.subs(y,5))
print('当y=2，z=3时，expr2=',expr2.subs({y:2,z:3}))# 以字典形式传入
print('当y=2，z=3时，expr2=',expr2.subs({y:2,z:3}).n())
x= sin(1)
x= 0.841470984807897
x= 0.8414709848078965
pi 3.14
expr1= y*sin(y**2)
当y=5时，expr1= 5*sin(25)
当y=2，z=3时，expr2= sin(2)*cos(2) + sin(3) + 4
当y=2，z=3时，expr2= 3.76271876040590
sympy有很多函数可以用于处理有理数。这些函数可以对有理数做简化，展开，合并等操作。为了计算两个有理数的加法，我们用together函数；类似的，有理数的除法我们用apart函数
例：together()和apart()使用示例
x1,x2,x3,x4=symbols('m1:5')
x=symbols('x')
print(x1/x2+x3/x4)
print(together(x1/x2+x3/x4))
print((2*x**2+3*x+4)/(x+1))
print(simplify((2*x**2+3*x+4)/(x+1))) #没有变化
print(apart((2*x**2+3*x+4)/(x+1)))
m1/m2 + m3/m4
(m1*m4 + m2*m3)/(m2*m4) #会帮你约分
(2*x**2 + 3*x + 4)/(x + 1)
(2*x**2 + 3*x + 4)/(x + 1) #直接化简没变化
2*x + 1 + 3/(x + 1) #一样，约分了
二.scipy工具库简介
SciPy是对NumPy的功能扩展，它提供了许多高级数学函数，例如微分、积分、微分方程、优化算法、数值分析、高级统计函数、方程求解等。SciPy是在NumPy数组框架的基础上实现的，它对NumPy数组和基本的数组运算进行扩展，满足科学家和工程师解决问题时需要用到的大部分数学计算功能。
SciPy支持的功能包括文件处理、积分、数值分析、优化方法、统计学、信号与图像处理、聚类分析和空间分析等。下面简要介绍部分功能模块
1.积分模块（scipy.integrate）
积分模块支持数值积分和微分方程数值解的功能
1.1给定函数的数值积分
- quad:一重数值积分
- dblquad:二重数值积分
- tplquad:三重数值积分
- nquad:通用n重积分
- fixed_quad:使用固定阶高斯求积公式求数值积分
- quadtature:使用固定误差限的高斯求积公式求数值积分
- romberg:求函数的Romberg数值积分
1.2 给定离散点的数值积分
- cumtrapz:用梯形法求数值积分
- simps：用辛普森法求数值积分
- romb:用Romberg积分法求自变量均匀间隔离散点的数值积分
1.3 微分方程的数值解
- odeint：使用Fortran库中方法求微分方程组的数值解
- ode: 求一般微分方程组的数值解
- complex_ode=求复微分方程组的数值解
2.线性代数模块（scipy.linalg）
与numpy.linalg相比，scipy.linalg函数有更高级的特征。
3.优化模块（scipy.optimize）
SciPy的优化模块提供了解决单变量和多变量的目标函数最小值问题的功能。它通过大量的算法解决最小化问题。优化模块支持线性回归、搜索函数的最大值与最小值、方程求根、线性规划、拟合等功能。
4.插值模块（scipy.interpolate）
插值模块支持一维和多维插值，例如泰勒（Taylor）多项式插值，一维和多维样条插值。
5.统计学模块（scipy.stats）
统计模块提供了各种随机变量的分布、统计量的计算、分布拟合、参数检验等功能。
6.傅里叶变换模块（scipy.fftpack）
离散傅里叶变换和离散傅里叶逆变换可以分别用fft和ifft函数来计算。
7.信号处理模块（scipy.signal）
信号处理模块包含一系列滤波函数、滤波器设计函数，以及对一维和二维数据进行B-样条插值的函数。这个模块包含的函数可以进行以下操作：卷积、B-样条、滤波、滤波器设计、MATLAB式的IIR滤波器设计、连续时间的线性系统、离散时间的线性系统、线性时不变系统、信号波形、窗函数、小波分析和光谱分析等。
8.多维图像处理模块（scipy.ndimage）
通常图像处理可以看作对二维数组的操作。这个模块提供了图像处理的各种函数，例如图像几何变换、图像滤波等。
9.空间分析模块（scipy.spatial）
空间分析是一系列用于分析空间数据的算法。空间数据是指和地理空间或垂直空间相关的数据对象。这种数据包括点、线、多边形、其他几何和地理特征信息。
该模块支持Delaunay三角剖分、Voronoi图、 维凸包等功能，支持KD树（scipy.spatial.kdtree）实现快速近邻查找算法，还可以对初始向量集合进行距离矩阵的计算。
10.聚类模块（scipy.cluster）
聚类是将一个大的集合分成多个组的过程。SciPy聚类模块包括两个子模块：向量量化（Vector Quantization，VQ）（scipy.cluster.vq）和层次聚类（scipy.cluster.hierarchy）。VQ模块支持K-means聚类和向量量化，层次聚类模块支持分层聚类和聚合聚类。
11.文件输入/输出模块（scipy.io）
该模块支持一系列格式文件的读和写。这些格式文件包括：MATLAB文件、ALD文件、Matrix Market文件、无格式的FORTRAN文件、WAV声音文件、ARFF文件和NetCDF文件。
SciPy可以使用MATLAB的.mat文件格式读取和写入数据，函数为loadmat和savemat。如果要加载数据，则可以使用如下语法：
import scipy.io
data=scipy.io.loadmat('datafile.mat')
返回值data为一个字典，该字典包含了与.mat文件中保存的变量名相对应的键，对应值为NumPy数组格式。
保存数据到.mat文件涉及创建一个包含要保存的所有变量的字典（变量名和值），函数为savemat，保存数组x和y的代码如下：
data={}; data['x']=x; data['y']=y
scipy.io.savemat('datafile.mat',data)
还有其他一些模块：如附件模块（scipy.misc），实现图形读写操作功能；稀疏矩阵及其相关算法模块（scipy.sparse）；特殊函数模块（scipy. special）等。
三、用sympy做符号函数画图
用sympy做符号函数画图很方便，下面通过一些例子来说明二维图形、三维图形和隐函数符号函数画图方法
1.二维曲线画图
plot的基本使用格式
plot(表达式,变量取值范围,属性=属性值)
plot(表达式1，表达式2，变量取值范围,属性=属性值)
或者
plot((表达式1，变量取值范围)，(表达式2，变量取值范围))
在同一图形界面上画出y1=sinx,x属于[-6,6],y2=cos(x+pi/4)，x属于[-5,5]
from sympy import *
plot((2*sin(x),(x,-6,6)),(cos(x+pi/4),(x,-5,5)))
2.三维曲线画图
例子：画出三维曲面z=sin(sqrt(x2+y2))的图形
from pylab import rc #pylab为matplotlib的接口
from sympy.plotting import plot3d
from sympy.abc import x,y #引进符号变量x,y
from sympy.functions import sin,sqrt
rc('font',size=16); rc('text',usetex=True)
plot3d(sin(sqrt(x**2+y**2)),(x,-10,10),(y,-10,10),xlabel='$x$',ylabel='$y$')
3.隐函数画图
例子：绘制(x-1)2+(y-2)2-4=0的图形
from pylab import rc
from sympy import plot_implicit as pt,Eq
from sympy.abc import x,y #引进符号变量x,y
rc('font',size=16); rc('text',usetex=True)
pt(Eq((x-1)**2+(y-2)**3,4),(x,-6,6),(y,-2,4),xlabel='$x$',ylabel='$y$')
#转化成(x-1)^2+(y-2)^3=4的形式，Eq为隐函数画图标志
或者使用匿名函数画图
from sympy import plot_implicit as pt
from sympy.abc import x,y #引进符号变量x,y
ezplot=lambda expr:pt(expr)
ezplot((x-1)**2+(y-2)**3-4)
四、高等数学问题的符号解
SymPy包括许多功能，从基本的符号算术到多项式、微积分、求解方程、离散数学和统计等。它主要处理三种类型的数据：整型数据、实数和有理数。有理数包括两个部分：分子和分母，可以用Ration类定义有理数。本节通过示例程序来理解SymPy的概念及应用。
1.求极限
验证sinx/x在趋于0的极限等于0，（1+1/x）^x在X趋于无穷极限为e
from sympy import *
x=symbols('x')
print(limit(sin(x)/x,x,0))
print(limit(pow(1+1/x,x),x,oo))
1
E
2.求导数
已知z=sinx+x2*ey，求对x的二阶导和对y的一阶导
from sympy import *
x,y=symbols('x y')#定义两个符号变量
z=sin(x)+x**2*exp(y)# 构造符号表达式
print('关于x的二阶偏导数为：',diff(z,x,2))
print('关于y的一阶偏导数为：',diff(z,y,1))
关于x的二阶偏导数为： 2*exp(y) - sin(x)
关于y的一阶偏导数为： x**2*exp(y)
3.级数求和
验证k平方从1到n求和为 n*(n+1)*(2n+1)/6。以及1/k^2 从1到无穷求和为 pi^2/6
k,n=symbols('k n')
print(summation(k**2,(k,1,n)))
print(factor(summation(k**2,(k,1,n)))) #把计算结果因式分解
print(summation(1/(k**2),(k,1,oo)))
n**3/3 + n**2/2 + n/6
n*(n + 1)*(2*n + 1)/6
pi**2/6
4.泰勒展开
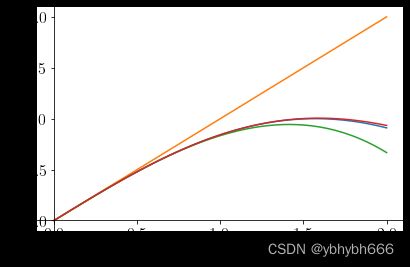
写出sinx在0点处的3,5,7阶泰勒展开式，并在同一图形界面上画出sinx及它的上述各阶泰勒展开式在区间[0,2]上的图形
from pylab import rc
from sympy import *
rc('font',size=16);rc('text',usetex=True)
x=symbols('x');y=sin(x)
for k in range(3,8,2):
print(y.series(x,0,k))# 在0处的k阶泰勒展开，等价于print(series(y,x,0,k))
plot(y,series(y,x,0,3).removeO(),series(y,x,0,5).removeO(),series(y,x,0,7).removeO(),(x,0,2))
x + O(x**3)
x - x**3/6 + O(x**5)
x - x**3/6 + x**5/120 + O(x**7)
5.不定积分和定积分 integrate
验证sin(2x)在[0,pi]上的积分=0，sinx/x在[0,+oo]上积分为pi/2
from sympy import *
x=symbols('x')
print(integrate(sin(2*x),(x,0,pi)))
print(integrate(sin(x)/x,(x,0,oo)))
0
pi/2
6.求解代数方程（方程组）的符号解 solve
6.1求解如下方程 x3=1,(x-2)2(x-1)^3=0
x,y=symbols('x y')
print(solve(x**3-1,x))
print(solve((x-2)**2*(x-1)**3,x))
print(roots((x-2)**2*(x-1)**3,x))#可以得到根的重数信息
[1, -1/2 - sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]
[1, 2]
{2: 2, 1: 3}
6.2 求如下方程组 x2+y2=1 ∩ x-y=0
print(solve([x**2+y**2-1,x-y],[x,y]))
[(-sqrt(2)/2, -sqrt(2)/2), (sqrt(2)/2, sqrt(2)/2)]
6.3 求函数f(x)=2*x3-5*x2+x 的驻点，并求函数在0，1上的最大值
from sympy import *
x=symbols('x')
y=2*x**3-5*x**2+x
x0=solve(diff(y,x),x) #驻点
print('驻点为:',x0)
print('驻点的浮点数表示为:',[x0[i] for i in range(len(x0))]
驻点为: [5/6 - sqrt(19)/6, sqrt(19)/6 + 5/6]
驻点的浮点数表示为: [0.106850176076554, 1.55981649059011]
y0=[y.subs(x,0),y.subs(x,1),y.subs(x,x0[0].n())] #第二个驻点不在范围内，计算端点和驻点的值
max(y0)
0.0522051838383851
7.求微分方程的符号解
sympy 库提供了dsolve函数求常微分方程的符号解
在声明时，要使用Function函数
y=Function('y')
y=symbols('y',class=Function)
7.1 求下列微分方程的通解。(1)y’‘-5y’+6y=0 (2)y’‘-5y’+6y=x*e^2x
x=symbols('x')
y=Function('y')
eq1=diff(y(x),x,2)-5*diff(y(x),x,1)+6*y(x)
eq2=diff(y(x),x,2)-5*diff(y(x),x,1)+6*y(x)-x*exp(2*x)
print('齐次方程解为:',dsolve(eq1,y(x)))
print('非齐次方程解为:',dsolve(eq2,y(x)))
齐次方程解为: Eq(y(x), (C1 + C2*exp(x))*exp(2*x))
非齐次方程解为: Eq(y(x), (C1 + C2*exp(x) - x**2/2 - x)*exp(2*x))
7.2 带有初值问题的：y’‘-5y’+6y=0 ,y(0)=1,y’(0)=0
print("初值问题的解为：{}".format(dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0})))
初值问题的解为：Eq(y(x), (3 - 2*exp(x))*exp(2*x))
五、高等数学问题的数值解
大多数实际问题是无法求符号解的，只能求数值解，即近似解。本节介绍调用SciPy工具库求数值解，其中的一些问题我们自己设计Python程序。
已经知道sin(x)的泰勒级数展开为sin(x)=Σ（-1）k*x(2k+1)/(2k+1)!
画出sinx以及它在0点处的1，3，5阶泰勒展开式，在x∈[-2pi,2pi]的图形
编写如下的函数mysin求 的近似值。调用自定义函数mysin画出泰勒展开式的图形，设计程序如下：
import numpy as np
import matplotlib.pyplot as plt
def fac(n):return (1 if n < 1 else n*fac(n-1)) #n的阶乘
def item(n,x):return (-1)**n*x**(2*n+1)/fac(2*n+1) #sinx的泰勒展开公式
def mysin(n,x): return (0 if n<0 else mysin(n-1,x)+item(n,x)) #用递归求和
x=np.linspace(-2*np.pi,2*np.pi,101)
plt.plot(x,np.sin(x),'*-')
str=['v-','H--','-.'] #画图的符号
for n in [1,2,3]:
plt.plot(x,mysin(2*n-1,x),str[n-1])
plt.legend(['sin','n=1','n=3','n=5'])
plt.show()
2.数值导数
讲一个运动学的例子：甲、乙、并、丁4个人分别位于起始位置 、 、 以及 处（单位：米），并且以恒定的速率1（单位：米/秒）行走。在行走过程中，甲始终朝向乙的当前位置；同样，乙朝向丙、丙朝向丁、丁朝向甲。试绘制4人行走过程的近似轨迹
我们已知 v(t)=r’(t) 速度是位移相对于时间的导数
在很短的一段时间里有 r(t+Δt)≈r(t)+v(t)*Δt
他在xoy平面有
rx(t+Δt)≈rx(t)+v(t)Δtcosθ（t）
ry(t+Δt)≈ry(t)+v(t)Δtsinθ（t）
xy和xyn分别表示当前位置和下一位置四个人的位置，Txy[i]存放第i个人所有时刻的位置
import numpy as np, numpy.linalg as ng
import matplotlib.pyplot as plt
N=4; v=1.0; d=200.0; time=400.0; divs=201
xy=np.array([[-d,d],[d,d],[d,-d],[-d,-d]])
T=np.linspace(0,time,divs); dt=T[1]-T[0] #相当于Δt
xyn=np.empty((4,2)); Txy=xy #xyn先创建一个4*2的任意数字的数组，这样就不用初始化
for n in range(1,len(T)):
for i in [0,1,2,3]:
j=(i+1)%4;dxy=xy[j]-xy[i] #第i个人朝着下一个人的方向走
dd=dxy/ng.norm(dxy) #单位化一下 直接得出cos 和 sin
xyn[i]=xy[i]+v*dt*dd
Txy=np.c_[Txy,xyn]#这样可以把他们合起来在一个array里,变成四行n列，每一行数组代表一个人
xy=xyn.copy() #把刚才的一步更新
for i in range(N):plt.plot(Txy[i,::2],Txy[i,1::2]) #Txy中的第i个数组表示第i个人的所有轨迹，x1,y1,x2,y2这样，所以画图要跳着来
plt.show()
3.数值积分
3.1 一重积分用函数quad
例：求sinx*sqrt(cosx+x^2) 在0到1上积分
from scipy.integrate import quad
from sympy import *
f= lambda x:sin(sqrt(cos(x)+x**2))
print(quad(f,0,1))
跟之前的integrate不一样，这里是求近似解，integrate求不了近似解（应该把，反正integrate在这题用不了），要用quad只能用lambda定义（至少目前我只知道这个），如果单单用symbols（x） 然后让f等于…x 那样是不行的
3.2 多重积分
多重积分我们使用scipy库中的dblquad和tplquad直接求数值解
dblquad的调用格式为：
dblquad(func, a, b, gfun, hfun, args=(), epsabs=1.49e-08, epsrel=1.49e-08)
其中被积函数func的格式为func(y,x)，最外层x的积分区间为[a,b]，内层y的积分区间为[ gfun(x),hfun(x)]。
tplquad的调用格式为：
tplquad(func, a, b, gfun, hfun, qfun, rfun, args=(), epsabs=1.49e-08, epsrel=1.49e-08)
其中被积函数func的格式为func(z, y, x)，最外层x的积分区间为[a,b]，中间层y的积分区间为[gfun(x), hfun(x)]，最内层z的积分区间为[qfun(x,y),rfun(x,y)]。
计算0-2dx0-1(x*y**2)dy
from sympy import *
from scipy.integrate import dblquad
f1=lambda y,x:x*y**2
print(dblquad(f1,0,2,0,1))
要是积分上下限带有 符号如x,y的话，也要用lambda来表示上下限，如
import numpy as np
from scipy.integrate import tplquad
f=lambda z, y, x: z*np.sqrt(x**2+y**2+1)
ybd=lambda x: np.sqrt(2*x-x**2)
print("I=",tplquad(f, 0, 2, lambda x: -ybd(x),ybd, 0, 6))
4.非线性方程数值解
1.二分法求根
采用二分法对方程求根时,第n 次迭代对应的区间长度为 (b-a)/2^n,收敛速度是较快的.
2.牛顿迭代法求根
3.用scipy工具库求解非线性方程（组）
求 x3+1.1x2+0.9x-1.4=0 实根的近似值，使误差不超过 10^{-6}。要求使用三种方法：1.二分法 2.牛顿迭代法 3.直接调用Scipy库求解
import numpy as np
from scipy.optimize import fsolve
def binary_search(f, eps, a, b): #二分法函数
c=(a+b)/2
while np.abs(f(c))>eps:
if f(a)*f(c)<0: b=c
else: a=c
c=(a+b)/2
return c
def newton_iter(f, eps, x0, dx=1E-8): #牛顿迭代法函数
def diff(f, dx=dx): #求数值导数函数
return lambda x: (f(x+dx)-f(x-dx))/(2*dx)
df=diff(f,dx)
x1=x0-f(x0)/df(x0)
while np.abs(x1-x0)>=eps:
x1, x0=x1-f(x1)/df(x1), x1
return x1
f=lambda x: x**3+1.1*x**2+0.9*x-1.4
print("二分法求得的根为：", binary_search(f,1E-6,0,1))
print("牛顿迭代法求得的根为：",newton_iter(f,1E-6,0))
print("直接调用SciPy求得的根为：",fsolve(f,0))
二分法求得的根为： 0.6706571578979492
牛顿迭代法求得的根为： 0.6706573107258097
直接调用SciPy求得的根为： [0.67065731]
4. 用fsolve求非线性方程组的数值解
例3.22 求下列非线性方程组的数值解
from numpy import sin
from scipy.optimize import fsolve
f=lambda x: [5*x[1]+3, 4*x[0]**2-2*sin(x[1]*x[2]), x[1]*x[2]-1.5]#使用匿名函数，将三个方程表示出来
print("result=",fsolve(f, [1.0,1.0,1.0]))
上面的程序使用的是匿名函数，但是python下标从0开始，不太方便。下面利用函数定义方程组，使用起来更加方便一点：
from numpy import sin
from scipy.optimize import fsolve
def Pfun(x):
x1,x2,x3=x.tolist() #x转换成列表
return 5*x2+3, 4*x1**2-2*sin(x2*x3), x2*x3-1.5
print("result=",fsolve(Pfun, [1.0, 1.0, 1.0]))
5.函数极值点的数值解
例3.23 求函数f(x)=exp(x)*cos(2x)在区间[0,3]的极小点
from numpy import exp,cos
from scipy.optimize import fminbound
f=lambda x: exp(x)*cos(2*x)
x0=fminbound(f,0,3)
print("极小点为：{}，极小值为：{}".format(x0,f(x0)))
极小点为：1.8026199149262752，极小值为：-5.425165227463772
或者你也可以求在0附近的一个极小点
from numpy import exp,cos
from scipy.optimize import fmin
f=lambda x: exp(x)*cos(2*x)
x0=fmin(f,0)
print("极小点为：{}，极小值为：{}".format(x0,f(x0)))
Optimization terminated successfully.
Current function value: -0.234443
Iterations: 26
Function evaluations: 52
极小点为：[-1.339]，极小值为：[-0.23444265]
5.2. 多元函数的极值点
求函数的极小值
from scipy.optimize import minimize
f=lambda x: 100*(x[1]-x[0]**2)**2+(1-x[0])**2;
x0=minimize(f,[2.0, 2.0]) #2.0和2.0是我们设置的初始值
print("极小点为：{}，极小值为：{}".format(x0.x,x0.fun))
极小点为：[0.99999565 0.99999129]，极小值为：1.8932820837847567e-11
六、线性代数问题的符号解和数值解
1.线性代数问题的符号解
SymPy 线性代数模块的函数和矩阵操作都非常简单易学。它包括对矩阵的各种操作，例如,求矩阵行列式的值,特殊矩阵的构建,求矩阵的特征值、特征向量、转置和逆阵等。如利用eye,zeros和ones等函数,可以快速构造特殊矩阵。如果需要的话,可以删除矩阵中某些选中的行和列.基本算术运算,如＋,一,和*，也可以用于矩阵.
在符号矩阵运算中*表示矩阵乘积,**表示矩阵的幂运算。
1. 矩阵的运算
Python程序为
import sympy as sp
A=sp.Matrix([[1],[2],[3]]) #列向量,即3×1矩阵
B=sp.Matrix([[4],[5],[6]])
print("A的模为：",A.norm())
print("A的模的浮点数为：",A.norm().evalf())
print("A的转置矩阵为：",A.T)
print("A和B的点乘为：",A.dot(B))
python程序为
import sympy as sp
import numpy as np
A=sp.Matrix(np.arange(1,17).reshape(4,4))
B=sp.eye(4)
print("A的行列式为：",sp.det(A))
print("A的秩为：",A.rank())
print("A的转置矩阵为：",A.transpose()) #等价于A.T
print("所求的逆阵为：",(A+10*B).inv())
print("A的平方为：",A**2)
print("A,B的乘积为：",A*B)
print("横连矩阵为：",A.row_join(B))
print("纵连矩阵为：",A.col_join(B))
print("A1为：",A[0:2,0:2])
A2=A.copy(); A2.row_del(3)
print("A2为：",A2)
2. 解线性方程组
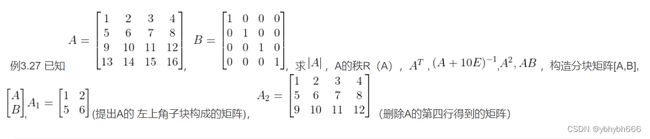
2.1求下列线性方程组的符号解
记上述线性方程组为Ax=b，可以验证系数矩阵A的秩R（A）=4，所以线性方程组有唯一解x=A^(-1)b
import sympy as sp
A=sp.Matrix([[2, 1, -5, 1],[1, -3, 0, -6],[0, 2, -1, 2],[1, 4, -7, 6]])
b=sp.Matrix([8, 6, -2, 2]); b.transpose()
print("系数矩阵A的秩为：",A.rank())
print("线性方程组的唯一解为：",A.inv()*b)
2.2、求下列齐次线性方程组的基础解系（齐次线性方程组：常数项全为0）
Python代码为
import sympy as sp
A=sp.Matrix([[1, -5, 2, -3],[5, 3, 6, -1], [2, 4, 2, 1]])
print("A的零空间（即基础解系）为：",A.nullspace())
2.3求下列非齐次线性方程组的通解
求通解首先要用rref()方法把增广阵化成行最简形
import sympy as sp
A=sp.Matrix([[1, 1, -3, -1],[3, -1, -3, 4], [1, 5, -9, -8]])
b=sp.Matrix([1, 4, 0]); b.transpose()
C=A.row_join(b) #构造增广矩阵
print("增广阵的行最简形为：\n",C.rref())
得到这个矩阵那答案就显而易见了吧
3. 特征值和特征向量
求下列矩阵的特征值和特征向量
要用到的Python函数有elgenvals()和elgenvects()
import sympy as sp
A=sp.Matrix([[0, -2, 2],[-2, -3, 4], [2, 4, -3]])
print("A的特征值为：",A.eigenvals())
print("A的特征向量为：",A.eigenvects())
可以看到 -8是一重特征根，1是二重特征根
4. 相似对角化
例子：把下列矩阵相似对角化，即求可逆矩阵P，使得P^(-1)AP=D为对角阵
第一个得到的矩阵是P，第二个是D
from sympy import Matrix, diag
A=Matrix([[0, -2, 2],[-2, -3, 4], [2, 4, -3]])
if A.is_diagonalizable(): print("A的对角化矩阵为：",A.diagonalize())
else: print("A不能对角化")
七、 线性代数问题的数值解（Numpy库）
以下都是用的array数组，运算和之前的可能会有所不同
1. 向量和矩阵的运算
python程序为
from numpy import arange, cross, inner
from numpy.linalg import norm
a=arange(1,4); b=arange(4,7) #创建数组
print("a的二范数为：",norm(a))
print("a点乘b=", a.dot(b)) #行向量a乘以列向量b
print("a,b的内积=",inner(a,b)) #a,b的内积,这里与dot(a,b)等价
print("a叉乘b=", cross(a,b))
python程序为
import numpy as np
import numpy.linalg as LA
A=np.arange(1,17).reshape(4,4)
B=np.eye(4)
print("A的行列式为：", LA.det(A))
print("A的秩为：",LA.matrix_rank(A))
print("A的转置矩阵为：\n",A.transpose()) #等价于A.T
print("所求的逆阵为：\n",LA.inv(A+10*B))
print("A的平方为：\n",A.dot(A))
print("A,B的乘积为：\n",A.dot(B))
print("横连矩阵为：",np.c_[A,B])
print("纵连矩阵为：",np.r_[A,B])
print("A1为：",A[0:2,0:2])
A2=A.copy(); A2=np.delete(A2,3,axis=0)
print("A2为：",A2)
2.齐次线性方程组的数值解
例3.35 求下列齐次线性方程组的基础解系（齐次线性方程组：常数项全为0
使用null_space
import numpy as np
from scipy.linalg import null_space
A=np.array([[1, -5, 2, -3],[5, 3, 6, -1], [2, 4, 2, 1]])
print("A的零空间（即基础解系）为：",null_space(A))
3. 非齐次线性方程组的数值解
（1）唯一解情形
求下列线性方程组的符号解
python程序为
import numpy as np
import numpy.linalg as LA
A=np.array([[2, 1, -5, 1],[1, -3, 0, -6],[0, 2, -1, 2],[1, 4, -7, 6]])
b=np.array([[8, 6, -2, 2]]); b=b.reshape(4,1)
print("系数矩阵A的秩为：",LA.matrix_rank(A))
print("线性方程组的唯一解为：",LA.inv(A).dot(b)) #使用逆矩阵
print("线性方程组的唯一解为：",LA.pinv(A).dot(b)) #使用伪逆
print("线性方程组的唯一解为：",LA.solve(A,b)) #利用solve求解
（2）多解情形
下列非齐次线性方程组有无穷多解，求它的最小范数解
多解情况下用pinv(A)*b 会给出最小范数解
from numpy import array
from numpy.linalg import pinv
A=array([[1, 1, -3, -1],[3, -1, -3, 4], [1, 5, -9, -8]])
b=array([1, 4, 0]); b.resize(3,1)
x=pinv(A).dot(b) #求最小范数解
print("最小范数解为：",x)
（3）无解情况
求下列矛盾方程组的最小二乘解
同样，用pinv(A)dot(b)会给出最小二乘解
from numpy import array
from numpy.linalg import pinv
A=array([[1, 1],[2, 2], [1, 2]])
b=array([1, 3, 2]); b.resize(3,1)
x=pinv(A).dot(b) #求最小二乘解
print("最小二乘解为：",x)
4.特征值与特征向量
求下列矩阵的特征值和特征向量
array数组和之前用的方法不一样噢
import numpy as np
from numpy.linalg import eig
A=np.array([[0, -2, 2],[-2, -3, 4], [2, 4, -3]])
values, vectors=eig(A)
print("A的特征值为：",values)
print("A的特征向量为：",vectors)
当然，我觉得array数组求出来的解都很怪，要想解好像还是用上面那个Matrix
但这种也没错啦，我们可以验证一下
from numpy import array, dot
from numpy.linalg import eig,inv
A=array([[0, -2, 2],[-2, -3, 4], [2, 4, -3]])
values, vectors=eig(A)
check=dot(inv(vectors),A).dot(vectors)
print("check=\n", check)
八、求超定线性方程组的最小二乘解
这个还没学过…
import numpy as np
import numpy.linalg as LA
from matplotlib.pyplot import plot, rc, legend, show, savefig
x = np.array([0, 1, 2, 3])
y = np.array([-1, 0.2, 0.9, 2.1])
A = np.c_[x, np.ones_like(x)]
m, c = LA.lstsq(A, y, rcond=None)[0]
print(m,c); rc('font',size=16)
plot(x, y, 'o', label='原始数据', markersize=5)
plot(x, m*x + c, 'r', label='拟合直线')
rc('font',family='SimHei') #用来正常显示中文标签
rc('axes',unicode_minus=False) #用来正常显示负号
legend(); savefig("figure3_41.png",dpi=500); show()
求得的最小二乘解为m=1,c=-0.95
